Sampled Softmax训练方法数学原理思考以及代码实现

前言

• 基于表征(Representation)形式的文本匹配、信息检索、向量召回的方法总结（用于召回、或者粗排）
• 文本匹配开山之作-DSSM论文笔记及源码阅读（类似于sampled softmax训练方式思考）

前面两篇关于文本匹配的博客中，都用到了Sampled-softmax训练方法来加速训练，Sampled-softmax简单点来说，就是通过采样，来减少我们训练计算loss时输出层的运算量。从第一篇博客中的不知其然，到后面看到DSSM代码中Sampled softamax的知其然，这篇博客目的是在知其所以然，从Sampled softmax的数学原理思考，为什么DSSM中的训练代码可以这样写，代码还能怎么改进。

这段时间也一直在思考，如何才能不随波逐流，如何才能成为一名独当一面的算法工程师，我想对于一个问题的浅尝辄止肯定是远远不够的，不仅要知其然还要知其所以然，光是读懂这几篇论文是不够的，进一步的要理解代码工程实现，更进一步，去理解代码背后的数学原理，为什么代码这样做一定能保证结果正确或者收敛，了解了这些，我们才能够根据自己的想法去做优化，我想对于现在日益成熟的深度学习，难的可能不是如何实现，而是对于自己的实际场景去调整优化。

上面有点扯远了，回归正题，这篇博客主要基于Tensorflow官方对于Sampled softmax文档，建议大家有问题不懂的时候多看官方文档，写的非常通俗易懂，下面我就说说自己对Sampled Softmax数学原理的理解。

What is Candidate Sampling Tensorflow 官方文档

什么是Sampled Softmax

1、logits与softmax

当我们做分类问题时，假设我们需要分类的类别数为$|L|$，那么我们做法通常如下，假设我们的输入为$x$：

1. 神经网络最后一层输出层神经元个数为$|L|$,每个神经元输出分别表示各个类别的logits, 这里的 logits 其实代表的就是各个类别未经归一化的概率分布（也就是加起来不为1）,网络就是学习出一个映射$f_{\theta }(x)=logits$
2. 将上述输出的logits作为softmax的输入进行归一化操作，softmax的输出则是表示各个类别上的概率分布
3. 根据这个概率分布计算损失函数，如交叉熵损失

还是采用之前博客中的Query-Doc Softmax作为说明，从logtis进行softmax归一化公式如下：

• $\mathbf{q},\mathbf{d}$ 表示我们的输入，$f_{\theta }(\ast )$表示我们的模型，$f_{\theta }(\mathbf{q},\mathbf{d})$即是给定$\mathbf{q}$情况下，输出类别为$\mathbf{d}$的logits
• 我们注意分母中$\mathcal{D}$即为所有文档集合，也就是我们的总类别数$|L|$

这个公式的具体解释可以参考之前的两篇博客，下面分析一下上面这个公式，下面是重点：

• 当我们类别数非常大时，也就是$\mathcal{D}$非常大时，那么我们分母的计算量就会非常大，因为需要在整个类别全集上求和。比如假设我们有100W个文档，那么如果我们不做任何处理，对于每个Query，分母中我们就要计算对这100W个文档的logits，然后求和进行归一化，这样的训练速度我们是不能接受的。Sampled Softmax思想就是，从全部类别集合$\mathcal{D}$中采样出一个子集，比如100个，然后在子集上计算logits并进行softmax归一化
• 我们如果对每个类别logits加上一个与类别无关的常数，结果将不会变化。这个很好理解，当我们对每个logits均加上同一个常数K，那么分子分母可以约去这个常数K,结果不变
• 分母其实是一个归一化因子，如果看过PRML同学应该熟悉，有点类似于指数族分布中的partition function，分母与类别无关，因为分母中对整个类别集合进行了求和，给定输入后，分母归一化因子也就确定了。

从上面分析可以知道，我们的关键词是logits、softmax归一化。logits本质上就是未归一化的概率，softmax目的就是计算归一化因子(分母)，对logtis进行归一化，从而得到一个概率分布。问题就在于需要对整个类别集合$\mathcal{D}$计算logtis并求和，当类别集合比较大时（比如上面的Query-Doc预测，以及语言模型训练），计算量会非常大。

2、Sampled Softmax

Sampled Softmax的核心思想就在于 Sampled，既然类别全集太大，那么能不能采样一个类别子集，然后在计算在子集上的logtis然后进行softmax归一化呢？假设我们类别全集为$L$，输入为$(x,T_i)$，其中$T_i$就是我们的输入类别标签，那么我们可以在$L$上随机采样一个子集$S_i\subset L$，并且与我们的输入类别$T_i$，共同组成候选类别子集$C_i$
$$C_i=T_i\cup S_i$$

我们在训练模型时，只要在这个采样出来的$C_i$上计算logits和softmax就可以了，大大减少了计算量，加快训练过程。现在问题是：

• 当我们进行采样之后，各个类别logits应该如何计算，和使用类别全集时的logtis有什么对应关系？

Sampled Softmax背后的数学原理

从上面可以看出，当我们进行采样后，按理来说logtis计算方法也需要改变，这样才能最后得到正确的概率分布。前方公式预警！！！！

1、数学符号约定

• $(x,t_i)$ 表示我们的一个训练样本,$x$为输入模型的特征,$t_i$为标签，目标类别
• $P(y|x)$ 给定输入$x$，输出类别为$y$的条件概率
• $F(x,y)$ 给定输入$x$，输出类别为$y$的logtis,这里$F(\ast ,\ast )$其实表示的就是我们的模型
• $L$ 类别全集
• $Q(y|x)$ 采样函数，给定输入$x$，采样出类别$y$的概率
• $S_i$ 采样出来的类别子集

以上符号如果没有特殊说明，都表示是在类别全集上进行计算

2、logits与概率之间的关系

其中$K(x)$表示与类别$y$无关的常数，其实就是softmax计算出来的分母。推导也很简单：
$$P(y|x)=\frac{exp(F(x,y))}{{\sum }_{\hat{y}\in L}exp(F(x,\hat{y}))}$$
两边同时取$log$，可以得到
$$log(P(y|x))=F(x,y)-log(\sum _{\hat{y}\in L}exp(F(x,\hat{y})))=F(x,y)-K(x)$$

最后将$K(x)$移项则可以得到上式。即logits可以写成“$log(P(y|x))+const$”这种形式。为什么要推导出这个关系呢，且听后面分解~

3、采样出类别子集$S_i$的概率表示

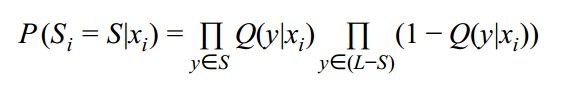
这里推导也很简单，当$y\in S_i$时概率为$Q(y|x_i)$，否则为$(1-Q(y|x_i))$,这里假设每次采样都是独立同分布(iid)，所以我们把每个类别概率乘起来就可以了

4、计算采样后类别子集$C_i$上的概率分布表示

重点来了！前面都是铺垫，我们最终的目的是计算给定输入$x$，在采样后的类别子集$C_i$概率分布表示，也就是
$$P(t_i=y|x,C_i)$$
进一步，由于在2中，logits与概率之间的关系，我们已经得到，所以我们就可以得到采样后logits的正确表示形式啦~，我们假设$C_i$为采样子集$S_i$和我们目标类别$t_i$的并集
$$C_i=S_i\cup \{t_i\}$$
那么在给定类别子集$C_i$，输入$x$条件下，输入类别$t_i=y$的概率$P(t_i=y|x,C_i)$计算推导如下，首先使用贝叶斯公式:

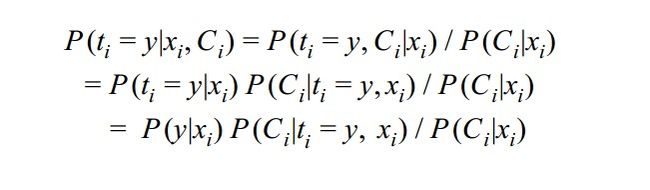
上面的推导就是简单的贝叶斯公式。我们分析一下推导结果：

• $P(y|x_i)$ 这个就是在类别全集情况下，给定输入$x$，输出类别为$y$的条件概率
• $P(C_i|t_i=y,x_i)$ 这个概率就是给定类别$y$，输入$x$情况下，采样出类别子集$C_i$的概率，这个计算方式已经在3中，采样出类别子集$S_i$的概率表示，推导出来如下
  
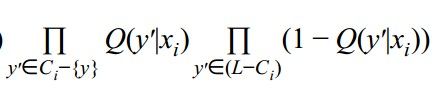
• $P(C_i|x_i)$ 这其实是个和输出类别$y$无关的常量,可以视为const

综上，下面$P(t_i=y|x,C_i)$计算结果如下:

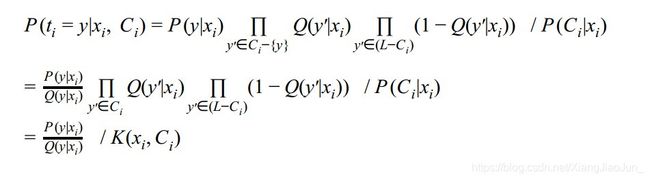
其中$K(x_i,C_i)$为与类别$y$无关的常数，我们对上式两边取$log$，则有：

结果已经跃然纸上，$Q(y|x_i)$是我们自己选取的采样函数，通过这个式子我们已经得到了采样后类别子集$C_i$和类别全集$L$上概率分布的关系

5、采样后类别子集$C_i$上的logits和原始logits关系

终于要到最后一步了，我们已经知道了采样后类别子集$C_i$和类别全集$L$上概率分布的关系，这时我们只需要利用2中的结论,logits与概率之间的关系,就可以得出采样后类别子集$C_i$上的logits和原始logits关系，推导如下：
$$log(P(t_i=y|x,C_i))=F(x,y|C_i)-K_1(x)$$
$$log(P(y|x))=F(x,y)-K_2(x)$$
带入上面推导出来的公式：
$$F(x,y|C_i)-K_1(x)=F(x,y)-K_2(x)-log(Q(y|x))+K^{‘}(x_i,C_i)$$
其中与类别$y$无关的常数项都可以合并，则有：
$$F(x,y|C_i)=F(x,y)-log(Q(y|x))+Const$$

大功告成！上面的公式就是我们进行采样后的logtis与原始logits关系，具体的用法如下：

• 通过$Q(y|x)$对类别进行采样，得到一个类别子集$C_i$
• 模型对采样类别子集$C_i$中的类别分别计算logits（这样就不用在类别全集计算logits了）,这里得到的其实是$F(x,y)$
• 对于计算出来的$F(x,y)$，减去$log(Q(y|x))$，就得到了我们采样后子集的logits，$F(x,y|C_i)=F(x,y)-log(Q(y|x))$
• 使用$F(x,y|C_i)$作为softmax输入，计算概率分布以及loss进行梯度下降

DSSM Sampled Softmax 分析

从上面分析可以得到：
$$F(x,y|C_i)=F(x,y)-log(Q(y|x))+Const$$

我们选取不同的采样函数$Q(y|x)$，那么结果也会不同，比如Tensorflow中有如下采样方式：

• tf.nn.log_uniform_candidate_sampler,按照 log-uniform (Zipfian) 分布采样。
  
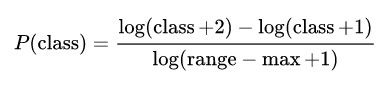
• tf.nn.learned_unigram_candidate_sampler 按照训练数据中类别出现分布进行采样。具体实现方式:1)初始化一个 [0, range_max] 的数组, 数组元素初始为1; 2) 在训练过程中碰到一个类别，就将相应数组元素加 1；3) 每次按照数组归一化得到的概率进行采样。

上述采样方式都和输入$x$相关，而如果我们选择随机采样，那么选择每个类别的概率都相等，也就是说$log(Q(y|x))$对于每个类别来说都一样，可以看做一个常数，并到后面常数项中，所以有：
$$F(x,y|C_i)=F(x,y)+Const$$
而上面分析过，logits加上或者减去一个常数，对softmax结果并没有影响,所以可以用原始logits代替采样后的logits。所以DSSM代码中，构造子集后直接计算logits然后做softmax结果也是正确的，代码如下：

with tf.name_scope('Loss'):
    # Train Loss
    # 转化为softmax概率矩阵。
    prob = tf.nn.softmax(cos_sim)
    # 只取第一列，即正样本列概率。相当于one-hot标签为[1,0,0,0,.....,0]
    hit_prob = tf.slice(prob, [0, 0], [-1, 1])
    loss = -tf.reduce_sum(tf.log(hit_prob))
    tf.summary.scalar('loss', loss)

总结

理论指导实践，代码中每一步都是有理论依据的，所以只有弄懂其背后的数学原理才能各个算法活学活用。以上也都是我的个人理解，难免有错，欢迎大家和我讨论，一起学习，一起进步~