深度神经网络结构以及Pre-Training的理解

http://www.cnblogs.com/neopenx/p/4575527.html

Logistic回归、传统多层神经网络

1.1 线性回归、线性神经网络、Logistic/Softmax回归
线性回归是用于数据拟合的常规手段，其任务是优化目标函数：h(θ)=θ+θ1x1+θ2x2+….θnxn

线性回归的求解法通常为两种：

①解优化多元一次方程（矩阵）的传统方法，在数值分析里通常被称作”最小二乘法”，公式θ=(XTX)−1XTY

②迭代法：有一阶导数（梯度下降）优化法、二阶导数（牛顿法）。

方程解法局限性较大，通常只用来线性数据拟合。而迭代法直接催生了用于模式识别的神经网络诞生。

最先提出Rosenblatt的感知器，借用了生物神经元的输入-激活-传递输出-接受反馈-矫正神经元的模式，将数学迭代法抽象化。

并且在线性回归输出的基础上，添加了输出校正，通常为阶跃函数，将回归的数值按正负划分。

为了计算简单，此时梯度下降优化法被广泛采用，梯度优化具有计算廉价，但是收敛慢的特点（一次收敛，而牛顿法是二次收敛)。

为了应对精确的分类问题，基于判别概率模型P(Y|X)被提出，阶跃输出被替换成了广义的概率生成函数Logistic/Softmax函数，从而能平滑生成判别概率。

这三个模型，源于一家，本质都是对输入数据进行线性拟合/判别，当然最重要的是，它们的目标函数是多元一次函数，是凸函数。

1.2 双层经典BP神经网络

由Hinton协提出多层感知器结构、以及Back-Propagation训练算法，在80年代~90年代鼎盛一时。

经过近20年，即便是今天，也被我国各领域的CS本科生、研究生，其他领域（如机械自动化）学者拿来吓唬人。

至于为什么是2层，因为3层效果提升不大，4层还不如2层，5层就太差了。[Erhan09]

这是让人大跌眼镜的结果，神经网络，多么高大上的词，居然就两层，这和生物神经网络不是差远了？

所以在90年代后，基于BP算法的MLP结构被机器学习界遗弃。一些新宠，如决策树/Boosing系、SVM、RNN、LSTM成为研究重点。

1.3 多层神经网络致命问题：非凸优化
这个问题得从线性回归一族的初始化Weight说起。线性家族中，W的初始化通常被置为0。

如果你曾经写过MLP的话，应该犯过这么一个错误，将隐层的初始化设为0。

然后，这个网络连基本的异或门函数[参考]都难以模拟。先来看看，线性回归和多层神经网络的目标函数曲面差别。

线性回归，本质是一个多元一次函数的优化问题，设f(x,y)=x+y

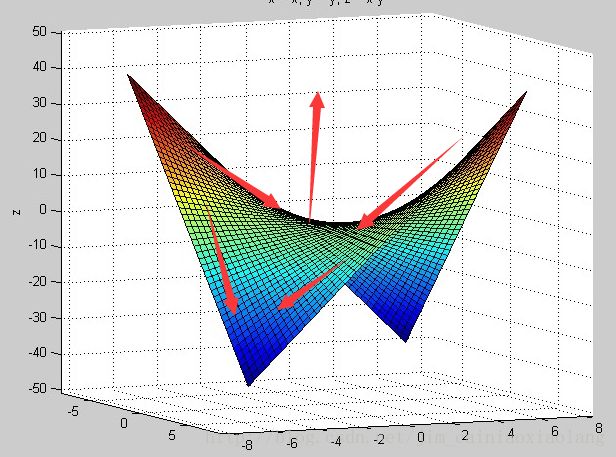
多层神经网络（层数K=2)，本质是一个多元K次函数优化问题，设f(x,y)=xy

值得一提的是，SVM是个K=2的神经网络，但是Vapnik转换了目标函数，将二次优化变成了二次规划。

相对于盲目搜索的优化问题，规划问题属于凸优化，容易搜到精确解。但是缺陷是，没人能将三次优化变成三次规划。

也就是说，K>=3的神经网络，如果训练到位，是可以轻松超越SVM的。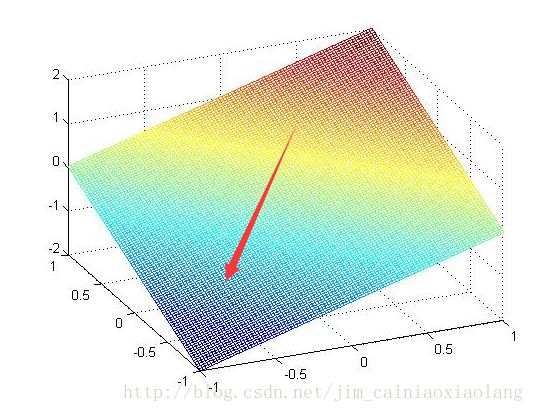

在线性回归当中，从任意一个点出发搜索，最终必然是下降到全局最小值附近的。所以置0也无妨。

而在多层神经网络中，从不同点出发，可能最终困在（stuck）这个点所在的最近的吸引盆（basin of attraction）。[Erhan09, Sec 4.2]

吸引盆一词非常蹩脚，根据百度的解释：它像一个汇水盆地一样,把处于山坡上的雨水都集中起来,使之流向盆底。

其实就是右图凹陷的地方，使用梯度下降法，会不自觉的被周围最近的吸引盆拉近去，达到局部最小值。此时一阶导数为0。从此训练停滞。

局部最小值是神经网络结构带来的挥之不去的阴影，随着隐层层数的增加，非凸的目标函数越来越复杂，局部最小值点成倍增长。[Erhan09, Sec 4.1]

因而，如何避免一开始就吸到一个倒霉的超浅的盆中呢，答案是权值初始化。为了统一初始化方案，通常将输入缩放到[−1,1]

经验规则给出，W∼Uniform(−1N√,1N√)

，Uniform为均匀分布。

Bengio组的Xavier在2010年推出了一个更合适的范围，能够使得隐层Sigmoid系函数获得最好的激活范围。[Glorot10]

对于Log-Sigmoid： [−4∗6√LayerInput+LayerOut√,4∗6√LayerInput+LayerOut√]

对于Tanh-Sigmoid： [6√LayerInput+LayerOut√,6√LayerInput+LayerOut√]

这也是为什么多层神经网络的初始化隐层不能简单置0的原因，因为0很容易陷进一个非常浅的吸引盆，意味着局部最小值非常大。

糟糕的是，随机均匀分布尽管获得了一个稍微好的搜索起点，但是却又更高概率陷入到一个稍小的局部最小值中。[Erhan10, Sec 3]

所以，从本质上来看，深度结构带来的非凸优化仍然不能解决，这限制着深度结构的发展。

1.4 多层神经网络致命问题：Gradient Vanish
这个问题实际上是由激活函数不当引起的，多层使用Sigmoid系函数，会使得误差从输出层开始呈指数衰减。见[ReLu激活函数]

因而，最滑稽的一个问题就是，靠近输出层的隐层训练的比较好，而靠近输入层的隐层几乎不能训练。

以5层结构为例，大概仅有第5层输出层，第4层，第3层被训练的比较好。误差传到第1、2层的时候，几乎为0。

这时候5层相当于3层，前两层完全在打酱油。当然，如果是这样，还是比较乐观的。

但是，神经网络的正向传播是从1、2层开始的，这意味着，必须得经过还是一片混乱的1、2层。（随机初始化，乱七八糟)

这样，无论你后面3层怎么训练，都会被前面两层给搞乱，导致整个网络完全退化，真是连鸡肋都不如。

幸运的是，这个问题已经被Hinton在2006年提出的逐层贪心预训练权值矩阵变向减轻，最近提出的ReLu则从根本上提出了解决方案。

2012年，Hinton组的Alex Krizhevsky率先将受到Gradient Vanish影响较小的CNN中大规模使用新提出的ReLu函数。

2014年，Google研究员贾扬清则利用ReLu这个神器，成功将CNN扩展到了22层巨型深度网络，见知乎。

对于深受Gradient Vanish困扰的RNN，其变种LSTM也克服了这个问题。
1.5 多层神经网络致命问题：过拟合
Bengio在Learning Deep Architectures for AI 一书中举了一个有趣的例子。

他说：最近有人表示，他们用传统的深度神经网络把训练error降到了0，也没有用你的那个什么破Pre-Training嘛！

然后Bengio自己试了一下，发现确实可以，但是是建立在把接近输出层的顶隐层神经元个数设的很大的情况下。

于是他把顶隐层神经元个数限到了20，然后这个模型立马露出马脚了。

无论是训练误差、还是测试误差，都比相同配置下的Pre-Training方法差许多。

也就是说，顶层神经元在对输入数据直接点对点记忆，而不是提取出有效特征后再记忆。

这就是神经网络的最后一个致命问题：过拟合，庞大的结构和参数使得，尽管训练error降的很低，但是test error却高的离谱。

过拟合还可以和Gradient Vanish、局部最小值混合三打，具体玩法是这样的：

由于Gradient Vanish，导致深度结构的较低层几乎无法训练，而较高层却非常容易训练。

较低层由于无法训练，很容易把原始输入信息，没有经过任何非线性变换，或者错误变换推到高层去，使得高层解离特征压力太大。

如果特征无法解离，强制性的误差监督训练就会使得模型对输入数据直接做拟合。

其结果就是，A Good Optimation But a Poor Generalization，这也是SVM、决策树等浅层结构的毛病。

Bengio指出，这些利用局部数据做优化的浅层结构基于先验知识（Prior）: Smoothness

即，给定样本(xi,yi)

，尽可能从数值上做优化，使得训练出来的模型，对于近似的x，输出近似的y。

然而一旦输入值做了泛型迁移，比如两种不同的鸟，鸟的颜色有别，且在图像中的比例不一，那么SVM、决策树几乎毫无用处。

因为，对输入数据简单地做数值化学习，而不是解离出特征，对于高维数据（如图像、声音、文本），是毫无意义的。

然后就是最后的事了，由于低层学不动，高层在乱学，所以很快就掉进了吸引盆中，完成神经网络三杀。