机器学习的一元线性回归最小二乘法

线性回归模型

线性回归（line regression）是一种线性模型，它假设输入变量x和单个输出变量y之间存在线性关系。
具体来说，利用线性回归，可以从一组输入变量x的线性组合中，计算输出变量y
y=ax+b

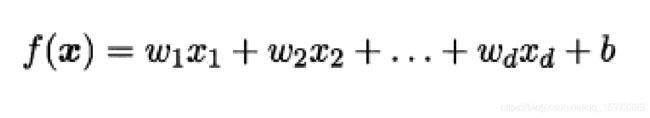
一般向量形式写成

最小二乘法

基于均方误差最小化来进行模型求解的方法为最小二乘法(least square method)，它的思想就是验证未知参数使得理论值和观测值之差的平方和达到最小。

在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧式距离之和最小。

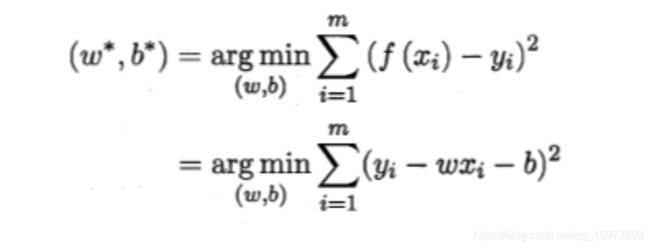
求解w和b就是使得E(w,b)最小化的过程。称为线性回归模型的“最小二乘参数估计”。求解过程，这里不展示，直接看结果。

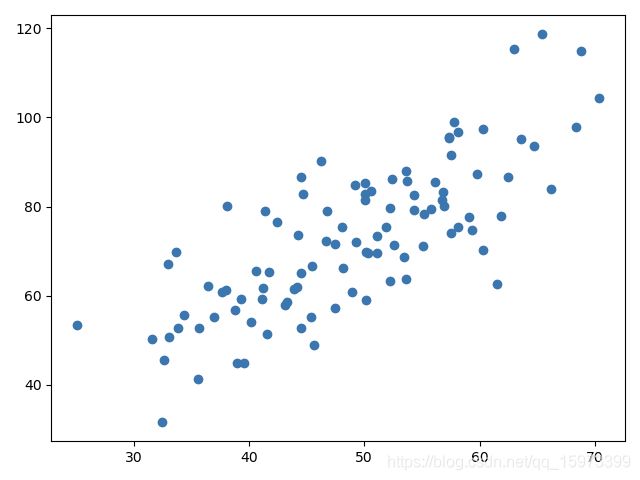
现在，有一组散点图，根据上述公式，求解直线。

Python实现

引用依赖

• numpy：NumPy（Numerical Python）是Python的一种开源的数值计算扩展。这种工具可用来存储和处理大型矩阵
• matplotlib：NumPy Matplotlib Matplotlib 是 Python 的绘图库。

代码讲解

1. 导入数据

import matplotlib.pyplot as plt
import numpy as np
points = np.genfromtxt('data.csv', delimiter=',')
print(points)

可以看到数据为一个二维数组，那么第一行的数据即points[0,0]，所有的x数据为points[:,0]，所有的y数据为points[:,1]

2. 散点图

x = points[:, 0]
y = points[:, 1]
plt.scatter(x, y)
plt.show()

3. 损失函数

需要计算平均均差，需要点的数量和系数w,b

def cost(wl, bl):
    total = 0
    for i in range(c):
        total += (y[i] - (wl * x[i] + bl)) ** 2
    return total / c

4. 拟合函数，求w和b

直接照公式完成。

# 拟合函数

def avg(d):
    total = 0
    for i in range(c):
        total += d[i]
    return total / c
    
def fit(xn, yn):
    # 所有x输入参数相加求平均值
    x_ = avg(xn)
    # 公式上半部分yx的求和
    sum_yx = 0
    sum_x2 = 0
    for i in range(c):
        sum_yx += yn[i] * (xn[i] - x_)
        sum_x2 += xn[i] ** 2
    wx = sum_yx / (sum_x2 - c * (x_ ** 2))

    sum_ywx = 0
    for i in range(c):
        sum_ywx += yn[i] - wx * x[i]
    bx = sum_ywx / c
    return wx, bx

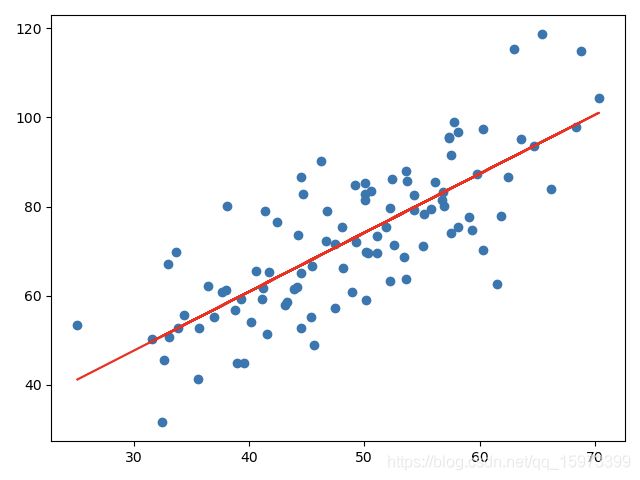
5. 散点图

# 测试
w, b = fit(x, y)
loss = cost(w, b)
print('w =', w)
print('b=', b)
print('loss=', loss)

# 画曲线
plt.scatter(x, y)
# 针对每一个x，计算出预测的y值
pred_y = w * x + b
plt.plot(x, pred_y, c='r')
plt.show()

计算结果：

w = 1.3224310227553846
b= 7.991020982269173
loss= 110.25738346621313

案例

我们利用线性回归来预测肥胖和高血压的具体关系，并给出如何预测自己是否具有高血压。
数据如下：

体重指数	血压mmHg
20.9	123
21.5	123
19.6	123
26	130
16.8	119
25.9	131
21.6	127

利用上面的算法，计算得出

w = 1.25799526855341
b= 97.7724743713308
loss= 1.378230964689395
预测体重指数24的血压： 127.96436081661264

等数据量多多时候，就会出现更合适的直线。