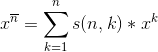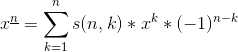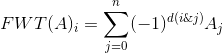20200521小结
(1)求数组(或矩阵)k次前缀和带修改
可以发现前缀和多次只是对原数组每一位对应乘上一个系数(其实就是组合数)
组合数可以转化为下降幂的形式,然后利用斯特林数转为普通幂,用k个树状数组维护ai*i^k之和即可
第一类斯特林数s上升幂\下降幂转普通幂
第二类斯特林数S普通幂转下降幂\上升幂
组合数的下降幂形式
或者暴力手动把下降幂多项式的系数乘出来也是可以的
例题
![]()
有一个很巧妙的性质,我们可以把矩阵中的值表示成列标号+(行标号-1)*m,只需要维护标号的k次前缀和,分开计算贡献即可
代码:
#include
#include
#include
using namespace std;
inline int gi()
{
char c;int num=0,flg=1;
while((c=getchar())<'0'||c>'9')if(c=='-')flg=-1;
while(c>='0'&&c<='9'){num=num*10+c-48;c=getchar();}
return num*flg;
}
#define N 100005
const int mod=1000000007;
int pw[N][11],s[11][11],fac[2*N],finv[2*N];
void shai()
{
int n=200000;
fac[0]=fac[1]=finv[0]=finv[1]=1;
for(int i=2;i<=n;i++){
fac[i]=1ll*i*fac[i-1]%mod;
finv[i]=1ll*(mod-mod/i)*finv[mod%i]%mod;
}
for(int i=2;i<=n;i++)
finv[i]=1ll*finv[i-1]*finv[i]%mod;
}
int C(int x,int y)
{
return 1ll*fac[x]*finv[y]%mod*finv[x-y]%mod;
}
int tra[2][11][N],n,m,Q;
void update(int x,int ad,int k,int flg)
{
int lim=(flg?m:n),p=pw[x][k];
while(x<=lim){
tra[flg][k][x]=(1ll*tra[flg][k][x]+1ll*ad*p)%mod;
x+=(x&-x);
}
}
int getsum(int x,int k,int flg)
{
int ret=0;
while(x){
ret=(1ll*ret+1ll*tra[flg][k][x])%mod;
x-=(x&-x);
}
return ret;
}
inline int rc(int x){return x&1?mod-1:1;}
int tmp[11],row[N],col[N];
char ch[3];
int main()
{
//freopen("1.in","r",stdin);
//freopen("1.out","w",stdout);
int i,j,k,x,y,z,w;
n=gi();m=gi();Q=gi();
s[0][0]=1;shai();
for(i=1;i<=10;i++){
s[i][0]=0;s[i][i]=1;
for(j=1;j=mod)sum1-=mod;
}
for(i=0;i<=k;i++)tmp[i]=(1ll*getsum(w,i,1)+1ll*mod-1ll*getsum(y-1,i,1))%mod;
for(i=0;i<=k;i++){
int sum=0,p=1;
for(j=0;j<=i;j++){
sum=(1ll*sum+1ll*rc(i-j)*C(i,j)%mod*p%mod*tmp[i-j])%mod;
p=1ll*p*(w+k)%mod;
}
sum=1ll*sum*s[k][i]%mod;
if((k-i)&1)sum=(mod-sum)%mod;
sum2+=sum;if(sum2>=mod)sum2-=mod;
}
ans=(1ll*sum1*C(k+w-y+1,k+1)%mod+1ll*sum2*C(k+z-x+1,k+1)%mod)%mod;
ans=(ans+mod)%mod;
ans=1ll*ans*finv[k]%mod;
printf("%d\n",ans);
}
else if(ch[0]=='R'){
x=gi();y=gi();
for(j=0;j<=10;j++){
update(x,(1ll*row[y]+1ll*mod-1ll*row[x])%mod,j,0);
update(y,(1ll*row[x]+1ll*mod-1ll*row[y])%mod,j,0);
}
swap(row[x],row[y]);
}
else{
x=gi();y=gi();
for(j=0;j<=10;j++){
update(x,(1ll*col[y]+1ll*mod-1ll*col[x])%mod,j,1);
update(y,(1ll*col[x]+1ll*mod-1ll*col[y])%mod,j,1);
}
swap(col[x],col[y]);
}
}
}
(2)西行寺无余涅槃 (20200521)
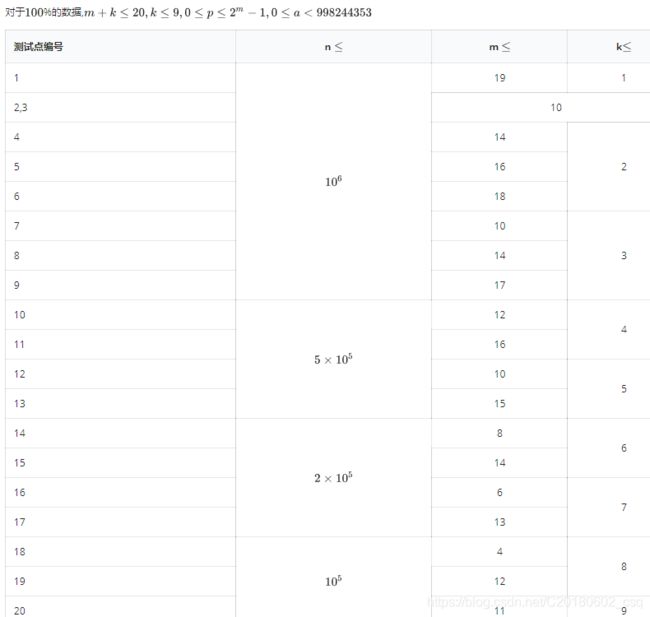
这题似乎没有2、3的数据点。。。
大致题意:
快速计算n个2^m次稀疏多项式的异或FWT卷积(最多只有10位有值,且权值种类也只有10种)
题解:
FWT神题
先考虑一个多项式异或FWT之后的结果:
发现每一位的结果只可能有2^k种
我们设在某一列这2^k种权值每种出现的次数分别为x0,x1,x2.......x_{2^k-1}
假设k=2
其中x0表示权值+a0+a1的出现次数
x1表示-a0+a1的出现次数
x2表示+a0-a1的出现次数
x3表示-a0-a1的出现次数
对于某一列,我们显然有x0+x1+x2+x3=n(一共有n个方程)
如果我们将每个方程中第p[i][0]项的系数+1
然后对这个新的多项式进行FWT就可以得到x0-x1+x2-x3在每一列的出现次数了
如果我们将每个方程中第p[i][1]项的系数+1再FWT可以得到x0+x1-x2+x3的出现次数
如果我们将每个方程中第p[i][0]^p[i][1]项的系数+1再FWT可以得到x0-x1-x2+x3的出现次数
(WTF???为什么啊啊啊????)
人类智慧结晶吧。。。。
然后我们依次类推,可以列出2^k-1个方程,加上第一个方程一共就有了2^k个方程
观察一下,发现这些方程放到一起再IFWT一下就可以解出每一个x再每一行的大小
(这TM谁看得出来啊。。。)
然后就用快速幂算出卷积结果,再IFWT一下解出最后结果
代码:(过于毒瘤)
#include
#include
#include
#include
using namespace std;
inline int gi()
{
char c;int num=0,flg=1;
while((c=getchar())<'0'||c>'9')if(c=='-')flg=-1;
while(c>='0'&&c<='9'){num=num*10+c-48;c=getchar();}
return num*flg;
}
#define N 1000005
const int mod=998244353;
const int inv2=499122177;
int n,m,K,a[21];
int A[N],lg[N],p[N][11],C[N];
vector >B;
void FWT(int *a,int len,int flg)
{
int i,j,k,X,Y;
for(i=1;i>=1;x=1ll*x*x%mod;
}
return ret;
}
vector tt;
int main()
{
int i,j,k,all,alk;
n=gi();m=gi();K=gi();
all=1<
(3)LCT维护多次询问的边加权最小生成树
对A树建最小生成树,作为初始状态的LCT
从小到大加入每一条B边,依次代替LCT每一条边,记录一下被替换的v权值下界以及答案的变化量
最后按照v权值下界排序再对答案变化量进行前缀和,二分一下v的位置即可回答每一个询问
正确性易证
代码:
#include
#include
#include
using namespace std;
inline int gi()
{
char c;int num=0,flg=1;
while((c=getchar())<'0'||c>'9')if(c=='-')flg=-1;
while(c>='0'&&c<='9'){num=num*10+c-48;c=getchar();}
return num*flg;
}
#define N 400005
#define LL long long
#define INF 0x3f3f3f3f
struct node{
int u,v,cd;
bool operator < (const node &t)const{return cdmx[x]){mx[x]=mx[lc];num[x]=num[lc];}
if(mx[rc]>mx[x]){mx[x]=mx[rc];num[x]=num[rc];}
}
void pushdown(int x){
if(rev[x]){
swap(ch[x][0],ch[x][1]);
if(lc)rev[lc]^=1;
if(rc)rev[rc]^=1;
rev[x]=0;
}
}
void rot(int x){
int y=fa[x],z=fa[y];bool flg=pdc(x);
if(nrt(y))ch[z][pdc(y)]=x;
if(ch[y][flg]=ch[x][flg^1])
fa[ch[y][flg]]=y;
ch[x][flg^1]=y;
fa[y]=x;fa[x]=z;
pushup(y);pushup(x);
}
void pdpath(int x){if(nrt(x))pdpath(fa[x]);pushdown(x);}
void splay(int x){
for(pdpath(x);nrt(x);rot(x))
if(nrt(fa[x]))rot(pdc(fa[x])==pdc(x)?fa[x]:x);
}
void Access(int x){
for(int i=0;x;i=x,x=fa[x]){
splay(x);
ch[x][1]=i;
pushup(x);
}
}
void beroot(int x){Access(x);splay(x);rev[x]^=1;}
void link(int x,int y){beroot(x);fa[x]=y;}
void cut(int x,int y){
beroot(x);Access(y);splay(y);
ch[y][0]=fa[x]=0;
pushup(y);
}
pair query(int x,int y){
beroot(x);Access(y);splay(y);
return make_pair(mx[y],num[y]);
}
}//----LCT----
int lian[N][2];
int main()
{
memset(LCT::mx,-0x3f,sizeof(LCT::mx));
memset(LCT::val,-0x3f,sizeof(LCT::val));
int n,A,B,Q,i,j,k=0,x;
n=gi();A=gi();B=gi();Q=gi();
for(i=1;i<=A;i++){e[i].u=gi();e[i].v=gi();e[i].cd=gi();}
for(i=A+1;i<=A+B;i++){e[i].u=gi();e[i].v=gi();e[i].cd=gi();}
sort(e+1,e+A+1);sort(e+A+1,e+A+B+1);
for(i=1;i<=n;i++)fa[i]=i;
LL ans=0;int ens=0;
for(i=1;i<=A;i++){
int p=find(e[i].u),q=find(e[i].v);
if(p!=q){
fa[q]=p;ens++;ans+=1ll*e[i].cd;
LCT::val[n+ens]=e[i].cd;
LCT::link(e[i].u,n+ens);LCT::link(e[i].v,n+ens);
lian[n+ens][0]=e[i].u;lian[n+ens][1]=e[i].v;
if(ens==n-1)break;
}
}
sum[0]=ans;tp[0]=-INF;
for(i=1;i<=n;i++)fa[i]=i;
for(i=A+1;i<=A+B;i++){
int p=find(e[i].u),q=find(e[i].v);
if(p!=q){
fa[q]=p;ens++;
pair tmp=LCT::query(e[i].u,e[i].v);
int pos=tmp.second;
LCT::cut(lian[pos][0],pos);LCT::cut(lian[pos][1],pos);
LCT::val[n+ens]=-INF;
LCT::link(e[i].u,n+ens);LCT::link(e[i].v,n+ens);
lian[n+ens][0]=e[i].u;lian[n+ens][1]=e[i].v;
sum[++k]=e[i].cd-tmp.first;
if(ens==2*n-2)break;
}
}
sort(sum+1,sum+k+1);
for(i=1;i<=k;i++)tp[i]=(sum[i]+1)>>1;
for(i=1;i<=k;i++)sum[i]+=sum[i-1];
for(i=1;i<=Q;i++){
x=gi();
j=upper_bound(tp+1,tp+k+1,x)-tp-1;
printf("%lld\n",sum[j]+1ll*(n-1-2*j)*x);
}
}
(4)FWT可以利用定义式单点展开某一个点的FWT结果
(5)powerful number求积性函数前缀和
黑科技powerful number
https://www.cnblogs.com/zzqsblog/p/9904271.html
本题就是构造一个G(p)=p^k ,然后写出其在狄利克雷卷积意义下的生成函数的闭形式,直接除一下就发现H(p^k)=p^k-p^2k
G的前缀和就用第二类斯特林数展开为下降幂即可
然后用dfs枚举powerful number直接算答案
然后TLE
有一个小优化,不要预处理幂和,因为有可能计算到非powerful number的幂和从而浪费时间
把每个powerful number的H之和记录下来,最后再来看哪些数要计算幂和
代码:
#include
#include
#include
#include
using namespace std;
#define N 300005
#define LL long long
#define id(i) (((i)<=lim)?id1[i]:id2[n/(i)])
LL id1[3200005],id2[3200005],a[2*3200005];
int lim,w[2*3200005],m;
const int mod=1000000007;
LL prime[N],tot,n,K;
bool vis[3200005];
int s[25][25],inv[25],pw[N],ppw[3200005];
inline int mihe(LL n)
{
if(n<=lim)return ppw[n];
int ret=0;n%=mod;
for(int i=1,su=n+1;i<=K;i++){
su=1ll*(n+1-i)*su%mod;
ret=(ret+1ll*s[K][i]*inv[i+1]%mod*su)%mod;
}
return ret;
}
inline int ksm(int x,int y)
{
int ret=1;
while(y){
if(y&1)ret=1ll*ret*x%mod;
y>>=1;x=1ll*x*x%mod;
}
return ret;
}
void shai()
{
LL i,j;lim=(LL)sqrt(n+0.5);
inv[0]=inv[1]=s[0][0]=1;
for(i=2;i<=21;i++)inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
for(i=1;i<=20;i++){
s[i][0]=0;s[i][i]=1;
for(j=1;jlim)break;
vis[tmp]=1;
if(i%prime[j]==0)break;
}
ppw[i]+=ppw[i-1];
if(ppw[i]>=mod)ppw[i]-=mod;
//mh[id(i)]=ppw[i];
}
}
int ans;
void dfs(int j,LL x,int h)
{
(w[id(n/x)]+=h)%=mod;
//ans=(1ll*ans+1ll*h*mh[id(n/x)])%mod;
for(int i=1;i<=j;i++){
LL p=prime[i]*prime[i];
if(x*p>n)break;
int th=1ll*h*pw[i]%mod;
for(;x*p<=n;p*=prime[i])
dfs(i-1,x*p,th);
}
}
//#include
int main()
{
//freopen("2.out","w",stdout);
scanf("%lld%lld",&n,&K);
//double c1=clock();
shai();
//printf("%.3fs\n",(clock()-c1)/1000);
//c1=clock();
dfs(tot,1,1);
//printf("%.3fs\n",(clock()-c1)/1000);
for(int i=1;i<=m;i++)
if(w[i])ans=(1ll*ans+1ll*w[i]*mihe(a[i]))%mod;
printf("%d\n",(ans+mod)%mod);
}
还有几道毒瘤题单独拿出来写