算法 前缀和与差分（一维二维）（幼稚园也能看懂的详解）

写在读前：
本文主要针对原理及如何实现，概念理解及方法或有偏差请多多指出并海涵~

一维前缀和

先来介绍前缀和：
顾名思义，前缀和便是计算这个元素及其前面元素的和，易与理解且实现简单，前缀和与差分的作用都是将区间运算化为点运算，降低时间复杂度，下面先讲一维前缀和后讲二维。

关于前缀和的介绍

不了解前缀和的同学可以先看一下这部分。
已知一数组a[]，可建立其前缀和数组sum[]，sum[1]代表a[]数组中到a[1]为止的所有元素的和,sum[2]到a[2]为止的所有元素的和,sum[3]代表到a[3]为止，以此类推，sum[n]代表a[n]及a[n]前所有元素的和。即：
sum[n] = a[1] + a[2] + … +a[n-1] + a[n] ；
这样，我们就将a[1],a[2],…,a[n]这个区间化为了点sum[n]，进而对点进行操作：

例：计算a[m]到a[n]所有元素的和：
普通方法便是开for循环 (int i=m;i 而建立了前缀和数组sum[]，之后便可以将时间复杂度缩短到1：
a[m]+a[m+1]+…+a[n] = sum[n] - sum[m-1]；
由于sum[n]代表从a[n]及a[n]之前所有元素和，a[m-1]代表a[m-1]及a[m-1]之前所有元素和，所以计算a[m]到a[n]便可以直接用sum[n]减去不需要的（a[m-1]以及a[m-1]前所有元素和）的部分，即减去sum[m-1]；
(注：是m-1不是m，若减去sum[m]计算的便是m+1到n之间所有元素的和)

实现前缀和操作

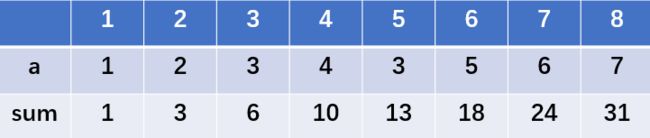
建立前缀和数组：

以上图为初始数组a[]，建立前缀和数组sum[]：
sum[1] = a[1] = 1 = sum[0] + a[1] ;
sum[2] = a[1] + a[2] = sum[1] + a[2] ;
sum[3] = a[1] + a[2] + a[3] = sum[2] + a[3] ;
…
sum[n] = sum[n-1] + a[n] ;

代码实现：

for(int i=1;i<=n;i++)
{
	 scanf("%d",&a[i]);
	 sum[i]=sum[i-1]+a[i];
}

利用前缀和实现运算：
由上文我们已经知道 a[m]+a[m+1]+…+a[n] = sum[n] - sum[m-1] 是利用前缀和计算的核心，下面举例证明：

例：计算a[2]到a[6]的和；
a[2] + a[3] + a[4] + a[5] + a[6] = 2 + 3 + 4 + 3 + 5 = 17 ;
sum[6] - sum[1] = 17 ;

代码实现：

int answer=sum[n]-sum[m-1];

二维前缀和

写在介绍前：
由前文可知一维前缀和是在一维的数轴上计算，而二维前缀和，顾名思义，便是在二维平面上计算，而相同的是，二维前缀和依然可以化区间计算为点子算，将（mn）的时间复杂度化为（1）。

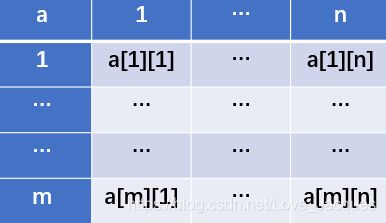
sum[m][n]的含义

由一维前缀和数组我们知道，在一维中sum[n]代表从a[0]到a[n]这条直线上所有元素的和，而二维的sum[m][n]便代表从a[0][0]、a[0][n]、a[m][0]、a[m][n]以这四点为顶点的矩形内所有元素的和。
即：
sum[m][n] =
a[0][0] + a[0][1] + … + a[0][n]+
a[1][0] + a[1][1] + … + a[1][n]+
…+
a[m][0] + a[m][1] + … + a[m][n]；

如何建立sum[][]

由一维前缀和的建立我们可知，sum[n] = sum[n-1]+a[n]，即前一个元素的sum与当前元素的a的和，而二维只不过比一维多了一个y轴上的分量，那么相加的时候将y轴上的分量也加上便可以了，这种想法到底适用不适用呢？

以上面左图的a数组为初始数组，我们经过手算得到正确的sum数组；下面验证sum到底该如何计算。

假设现在sum[5][6]未知，我们要计算sum[5][6]，由一维前缀和我们可以猜想sum[5][6]会不会等于sum[5][6-1] + sum[5-1][6] + a[5][6]？
但我们实际计算得到：
sum[4][6] + sum[5][5] + a[5][6] = 50 != sum[5][6]；

我们以sum[m][n]代表的含义来分析这个现象：

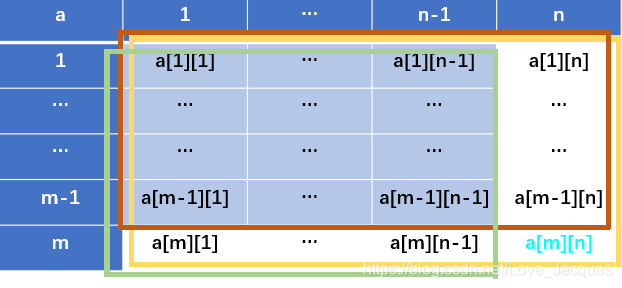
我们上述假设的公式为：sum[m][n] = sum[m-1][n] + sum[m][n-1] + a[m][n]；
但当我们仔细思考了sum[m][n]、与sum[m-1][n]、sum[m][n-1]的代表含义，sum[m][n-1]用绿框表示，sum[m-1][n]用棕框表示，sum[m][n]用黄框表示，之后便会发现用上述的计算方法会使得到的sum[m][n]的值多出一部分，便是绿框与棕框重合的部分，用蓝色底纹表示的矩形。
而结合sum[m][n]的含义我们很容易就能得到蓝色底纹矩形内所有元素和就是sum[m-1][n-1]。
此时我们便可以得到计算sum[m][n]的正确公式：
sum[m][n] = a[m][n] + sum[m-1][n] + sum[m][n-1] - sum[m-1][n-1]；
而得到了sum数组的递推公式，便可以实现sum数组的建立了。

代码实现：

for(int i1=1;i1<=m;i1++)
	for(int i2=1;i2<=n;i2++)
	{
	 	scanf("%d",&a[i1][i2]);
	 	sum[i1][i2]=a[i1][i2]+sum[i1-1][i2]+sum[i1][i2-1]-sum[i1-1][i2-1];
	}

如何利用sum[][]数组进行计算

我们已经知道了sum[m][n]代表的含义了，但这不是我们的最终目的，我们的目的是如来利用前缀和减少计算的时间复杂度。
建立了sum数组后，在一定预处理情况下便可以题目中求矩阵和的运算时间复杂度压缩到（1）。

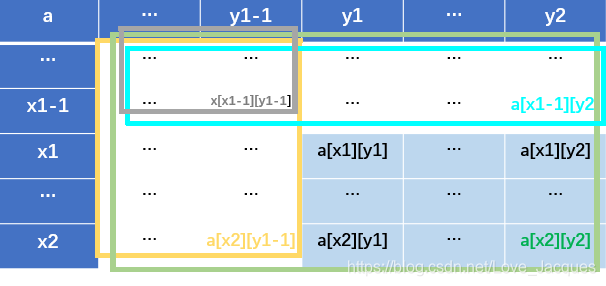
那么接下来举例说明如何求a[x1][y1]到a[x2][y2]区域内（淡蓝色底纹矩形）所有元素和：
想要计算此矩形的和，我们利用sum矩阵进行分块运算即可，前面我们已经充分了解了sum数组中各元素的含义，下面是他们发挥作用的时候了。

计算图中浅蓝色底纹矩阵我们理所当然的考虑它的四个顶点，其中sum[x2][y2]的可利用性最大，只需要减去绿框与浅蓝色矩形相比多余的部分即可得到所求答案；
我们根据 如何建立sum[][]中介绍的方法，如法炮制得到下面公式：
（即减去青色框与黄色框后多减了一个灰色框，需要再将灰色框加上）
矩阵内元素和=sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1] + sum[x1-1][x2-1]；

代码实现：

int answer=sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][x2-1];

一维差分

差分和前缀和：
前缀和是元素的累加，而差分则是相邻两元素的差；前缀和用来计算整块元素的和，而差分则用来实现整块元素的加或减（例如将a[m]到a[n]都+1）；
同样，差分也可以化区间计算为点计算，减小时间复杂度。

那么，差分数组到底有什么含义呢？

关于差分的介绍

diff[n]的含义，便是原始数组中当前项减去前一项的差。
即： diff[n] = a[n] - a[n-1] ；
而差分数组减小时间复杂度的原理类似于给每个需要操作的端点打上标记，多少次操作上多少次标记，最后一次性回收。
而打上标记的复杂度只有（1），一维数组中利用for循环的复杂度则为（n-m），二维数组更大，这便是diff数组减小时间复杂度的原理。

那么如何实现打上标记与标记回收呢？

实现差分操作

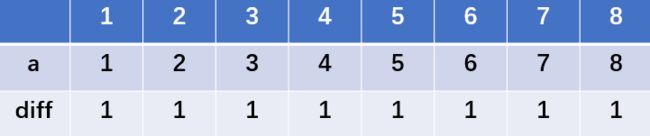
如上图，我们根据原始数组a[]建立了差分数组diff[]；
打上标记便是利用diff[]中元素的意义为两项之差来做文章，原理如下：
假设要求a[m]到a[n]内所有元素都 + c;

我们假设现在a数组已经进行了将a[m]到a[n]都+c的操作，那么原来的diff便不再准确，现在要更新diff数组，使其符合操作完成后的a数组。
根据diff[n] = a[n] - a[n-1]；我们可以知道区间 (m,n] 内所以元素的的diff值与原来的diff值相等，因为在diff[n] = a[n] - a[n-1]这个式子中，a[n]与a[n-1]同时进行了加或减操作。
而区间两端的diff值有所改变，例如m-1与m；a[m-1]为进行操作，而a[m]进行了操作，那么diff[m]便需要更新，这个更新的值便为c；
即：diff[m]+=c；
用diff数组的值来模拟a数组的变化；

这便是打上标记的一部分。

接下来我们先介绍如何回收标记：
上文说到，diff数组代替a数组进行操作，而差分数组又是由a数组两项相减得到的，由： diff[n] = a[n] - a[n-1] ；经过移项便得到：
a[n] = diff[n] + a[n-1]；
那么在所有标记都完成后，将替代a数组进行操作的diff[]纳入计算，来更新a[n]的过程，便是回收标记，即利用操作后的diff[n]值来更新a[n]值的连续过程。

为什么要叫做连续过程呢？
这是因为，从标记点开始往后，每一项a[n]都由diff[n]和前一项a[n-1]相加得到，而前一项又是由diff[n-1]和a[n-2]相加得到，退回到标记起始点，我们在这里对diff[起始点]进行了操作，使得a[起始点]的值发生了变化，进而影响了其后所有的a[n]值，那么如何结束这个影响呢？
这便是另一部分标记的任务；

既然diff[m]可以+=c，那么也就可以进行 diff[n+1] -=c ;
从而一直连续的过程到此，由于a[n-1]改变和diff[n]改变相抵消而结束。
将diff[n+1] -= c ; 便是另一部分标记。
注：我们可以通过控制diff[n]-=c的位置来控制过程结束的位置；即如果操作区间为m到n，则应进行的标记为diff[n+1] -= c，而不是在n

我们再来连续看一遍此过程：

对于a数组现在有四个操作：

1. a[1]到a[5] + 3;
2. a[2]到a[6] + 7;
3. a[1]到a[8] + 2；
4. a[3]到a[6] - 1；

先进行标记：
diff[1] += 3；diff[5+1] -= 3；
diff[2] += 7；diff[6+1] -= 7；
diff[1] += 2；diff[8+1] -= 2；
diff[3] += (-1)；diff[6+1] -= (-1)；

之后一次性更新a数组的值：
a[1] = a[0] + diff[1] = 6；
a[2] = a[1] + diff[2] = 14；
a[3] = a[2] + diff[3] = 14；
…
a[8] = a[7] + diff[8] = 1；

代码实现：

for(int i=1;i<=n;i++)//建立差分数组
{
	 scanf("%d",&a[i]);
	 diff[i]=a[i]-a[i-1];
}
while(k--)//k次操作，添加标记
{
	 scanf("%d%d%d",&l,&r,&c);//区间起点为l，终点为r，操作量为c
	 diff[l]+=c;
	 diff[r+1]-=c;
}
for(int i=1;i<=n;i++)//更新a数组，回收标记
	 a[i]=diff[i]+a[i-1];

二维差分

写在介绍前：
类似于一维前缀和于二维前缀和的关系，二维差分也只是一维差分延申除了一个y轴上的分量，将所有操作都考虑上y轴分量即可。

diff[m][n]的含义(以后再补)

如何建立diff[][]数组（未补）

如何利用diff[][]数组进行计算（未补）

总结

一维前缀和

建立：sum[n] = sum[n-1] + a[n]；
应用：a[n]+…a[m] = sum[m] - sum[n-1]；

二位前缀和

建立：sum[m][n] = sum[m-1][n] + sum[m][n-1] - sum[m-1][n-1] + a[m][n]；
应用：(x1,y1)到(x2,y2)内元素和 = sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1] + sum[x1-1][y1-1]；

一维差分

建立：diff[n] = a[n] - a[n-1]；
应用：diff[l] += c; diff[r+1] -= c; for(int i=1;i<=n;i++) a[n]=diff[n]+a[i-1]；

二维差分

建立：diff[m][n] = a[m][n]-a[m-1][n]-a[m][n-1]+a[m-1][n-1]；
应用：

void insert(int x1,int y1,int x2,int y2,int c)
{
	 val[x1][y1]+=c;
	 val[x2+1][y1]-=c;
	 val[x1][y2+1]-=c;
	 val[x2+1][y2+1]+=c;
	 return ;
}
for(int i1=1;i1<=m;i1++)
	 	 for(int i2=1;i2<=n;i2++)
	 	 	 a[i1][i2]=a[i1][i2-1]+a[i1-1][i2]-a[i1-1][i2-1]+val[i1][i2];

于2020.4.20第一次更新；