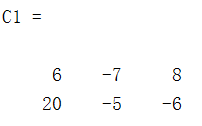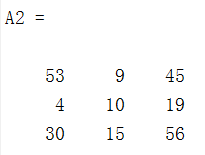matlab干货总结（二）基础学习篇之数组与矩阵

数组与矩阵篇：

一：数组

（一）：创建

1.用冒号创建

X=A:step:B 

---------A:创建一位数组的第一个变量；step：每次递增减的数值，直到最后一个元素和B的差的绝对值小于等于step的绝对值为止

2.用logspace函数创建（等比数列）

y=logspace(a,b)   ---创建行向量y，第一个元素，最后一个，总数为50个元素的等比数列。

y=logspace(a,b,n)   ---创建行向量y，第一个元素，最后一个，总数为n个元素的等比数列。

3.用linespace函数创建（线性间隔向量）

y=linespace(a,b)   ---创建行向量y，第一个元素a，最后一个b，总数为100个元素的线性间隔向量。

y=linespace(a,b,n)   ---创建行向量y，第一个元素a，最后一个b，总数为n个元素的线性间隔向量。

补充：向量的转置

例：B=[6 5 4 3 2 1 ]

E=B'   E为B的转置

 

（二）：运算

记住这句话即可：从每个单元出发，针对每个元素运算；包括加、减、乘、左除、右除、和乘方，当然维数必须一样

1：加

A+B

2：减

A-B

3;乘

A.*B

4;除

A./B=B.\A   ---A被除数，B除数

5：乘方

C=A.^B

6.点积

C=dot（A,B，维数）

补充：点积就是先对两个数字序列中的每组对应元素求积，再对所有积求和。

7：关系运算

正常的<、<=、>、>=、==、~=（不等于）

8.逻辑运算

与&、或|、非~

二：矩阵

（一）：创建

matlab中已经有各种定义好的特殊矩阵的函数，查询便知。其中个人认为比较重要的

1.希尔伯特矩阵：

（1）hilb(n):生成nxn希尔伯特

（2）invhilb(n):生成nxn希尔伯特逆矩阵整数矩阵

2.托普利兹矩阵：

（1）toeplitz(k,r):生成非对称托普利兹，非对称由行列向量定义

（2）toeplitz(c):生成对称托普利兹，单一向量即可定义

3.0~1间均匀分布随机矩阵

r=rand(m,n)   ---mxn型

4.标准正态分布随机矩阵

r=randn(m,n)

5.魔方阵（行列和对角线元素和相等）

M=magic(n)

6.帕斯卡矩阵

（1）A=pascal(n)   n阶正定帕斯卡，元素是帕斯卡三角组成

（2）A=pascal(n,1)   下三角Cholesky因子组成的帕斯卡，对称

补充：Cholesky分解是将一个正定的埃尔米特矩阵分解成一个下三角矩阵与其共轭转置之乘积。下三角Cholesky因子是分解后的因子。

（3）A=pascal(n,2)   (2)的转置和交换形式，且是单位阵的立方根。

7.范德蒙

A=vander（v）   列是v的幂

 

补充：上下合并：c=[a;b]   ；   左右合并：c=[a b]

 

（二）运算

1.加减

和线代计算原理相同，对应元素运算

         ---x为标量

2.乘法

条件与线代相同，维数不符合要求会报错

例

A=[2 1 4 0;1 -1 3 4];
B=[1 3 1;0 -1 2;1 -3 1;4 0 -2];
C1=A*B

3.除法

分左除右除，原理都一样，只不过像一枚硬币一样有反有正。

A\B ：A的逆乘B               A/B ：A乘B的逆

例

A=[1 2;1 3];
B=[1 0;1 2];
C1=A\B
C2=A/B

4.幂运算  ^

例

A=[2 3 8;3 1 -1;5 0 4]
A2=A^2
A6=A^6

5.求和

B=sum（A，dim）   ---dim为1时，计算各列元素和；为2时，计算各行元素和

B=cumsun    ----与上唯一不同是返回的是矩阵

 

6.求积

B=prod（A，dim）   ---dim不写或者写1时是各列元素积，为2时是各行元素的积

B=cumprod（A，dim） ---返回矩阵

7.差分

Y=diff（X，n，dim）  ---在维数dim上的n阶差分，dim=1算各列元素差分；dim=2算各行元素差分。

（三）稀疏矩阵

利用sparse函数将满阵转成稀疏阵

例

第一列记录第二列的元素位置，因为其余都是0

matlab中也有特殊稀疏矩阵的创建函数直接查询使用即可。

本人尚才疏学浅，如内容中有任何错误的地方，望告知，我会加以修改，之后会继续更新。