平衡树(splay)学习笔记(详细,从入门到精(bao)通(ling))(持续更新)
前言
在前几天军训站军姿的时候胡思乱想,突然明白了splay的本质
KMP学习笔记后又一篇字数上万的题解~
前置技能——二叉搜索树
首先来看一个最简单的问题:
你需要维护一个数据结构,资磁这些操作:
1.插入一个数
2.删除一个数
3.查询一个数 v v v是否在这个数据结构中
显然我们可以用一个桶记录某个数是否出现过,然后每个操作都是 O ( 1 ) O(1) O(1)的。(不管空间复杂度)
但是如果还需要资磁查询某个数的排名的操作,单次复杂度就不是 O ( 1 ) O(1) O(1),而是 O ( m a x ( v ) ) O(max(v)) O(max(v))了。( x x x的排名是指比 x x x小的数的个数+1)
所以我们需要引入一个数据结构:二叉搜索树。
二叉搜索树是一种奇妙的数据结构,它是一棵二叉树。
对于每个节点,它的左子树内的所有节点的权值都比它小,右子树内所有节点的权值都比它大。
简单地说,就是左<根<右。(注意这里“左”和“右”指子树而不是孩子)
最初,我们在二叉搜索树中插入正无穷、负无穷。
有了这个数据结构,我们珂以便捷地得到某个数 v v v的排名:
对这棵二叉搜索树进行dfs。
如果 v v v比当前节点权值大且当前节点有左孩子,就向左子树搜索;
如果 v v v比当前节点权值小且当前节点有右孩子,就向右子树搜索;
否则停在这个节点上。
不难发现,最后停在的节点是所有权值 > = x >=x >=x的节点中权值最小的节点(有点绕,思考一下)。
那么所有权值 < x
所以我们对于每个节点,维护一个子树大小 s i z siz siz,然后就珂以查出 x x x的排名辣qwq
然后我们发现,这个二叉搜索树比较神奇,它蜃至珂以求出 x x x的前后缀!
(前缀:小于 x x x的数中的最大的数;后缀:大于 x x x的数中的最小的数)
同样按照上面的dfs方法找到所有权值 > = x >=x >=x的节点中权值最小的节点。
如果我们想求前缀,就找到当前节点左子树中最大的节点(因为左<根<右)
如果我们想求后缀,若当前节点的权值 > x >x >x,后缀就是当前节点。否则后缀是右子树中最小的节点(同样因为左<根<右)
找二叉搜索树的权值最值也很简单,最小值就一直向左搜索,最大值就一直向右搜索,直到没有左/右孩子为止qwq
引入旋转操作
虽然二叉搜索树很吼,但我们发现二叉搜索树的复杂度仍然是不正确的。
看下面这个图:
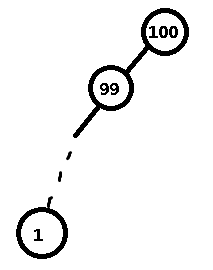
二叉搜索树的复杂度其实是 O ( h ) O(h) O(h), h h h表示树高。那么极限情况下是 O ( n ) O(n) O(n)的(一条链)
那么能不能让这棵树尽量平衡,变成一棵平衡树呢?
这里需要引入旋转操作。
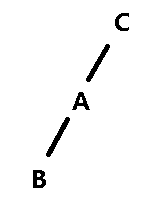
假设现在有一棵这样的二叉搜索树:

根据二叉搜索树性质,权值满足: X < B < Y < A < C . X
然后,我们把树绕着B旋转一下(珂以想象把B向上提的过程qwq)

我们惊奇地发现,B竟然有了3个孩子?
现在我们考虑怎样把B的某个孩子接到另一个孩子上,且不会破坏二叉搜索树性质。
因为 X < B < Y < A < C X
然后树变成介个样子:

这是B是A的左孩子的情况。
如果B是A的右孩子,操作方法也是差不多的,这里不作赘述。
回顾旋转过程:
假设现在要把节点 x x x向它的父亲旋转。( x x x到父亲方向:是左孩子还是右孩子)
假设原来多余的边自动断开(代码实现时,因为孩子只有2个,所以直接修改孩子编号即可,不用管多余的边)。
第一步: x x x的与 x x x到父亲方向相反的孩子向 x x x的父亲连边。
第二步: x x x的父亲向 x x x连边。
第三步:(前面没有提到) x x x向原来 x x x的父亲的父亲连边。
容易发现,旋转之后 x x x会出现在原来 x x x父亲的位置。
splay+双旋操作
splay的实现和二叉搜索树的实现大致相同,其中splay会多出旋转操作。
每次旋转操作时,我们会把某个节点不断旋转到根,以此来增加树结构的随机性。
但是旋转时,有一种情况可能会让树高增加。
假设有一棵树长这样
如果把B旋转两次,那么B确实会旋转到根,如图:
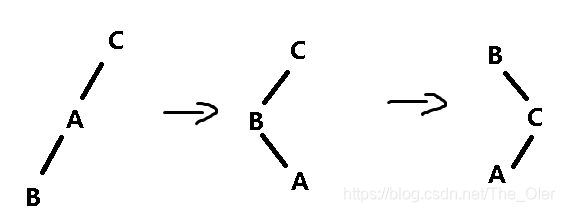
但是我们发现,两次旋转之后只是换了顺序,树高依然不变。
这种只旋转需要宣传到根的节点的旋转方法称为单旋。
珂以看出,单旋在节点到父亲的方向,和父亲到爷爷的方向一致时,树高不会改变(仍然是一条链),也就不能降低复杂度(单旋复杂度应该仍然是 O ( n ) O(n) O(n),但数据水的话一般跑不满)
所以这里用双旋:
双旋,就是节点到父亲、父亲到爷爷方向一致时,先旋转父亲,再旋转自己;当方向不一致时,旋转自己两次的旋转方式。
当树高 > 3 >3 >3时,就珂以发现splay完树高减少,这里因为懒,就不放图了qwq
洛谷P3369 普通平衡树
由Splay复杂度证明可知,单次操作是 O ( l o g n ) O(logn) O(logn)的。
所以洛咕P3369就珂以A掉了qwq,解析如下。
普通平衡树中的部分操作解析
声明变量
#define lc(x) w[x].ch[0]
#define rc(x) w[x].ch[1]
struct node {
int father; //父亲
int val,siz; //val表示权值,siz表示子树大小
int ch[2]; //ch[0]是左孩子,ch[1]是右孩子
int cnt; //表示这个值出现了几次
} w[Size];
int cnt,root; //cnt表示splay树中有几个节点,root表示树根
一些基本操作
pushup:维护 x x x的子树大小信息。
chk:判断 x x x到父亲的方向(左/右)
connect: x x x到 f a fa fa连一条边,且 x x x到父亲的方向是 k k k
NewNode:新建一个节点并返回其编号
inline void pushup(int x) { //维护子树大小信息
w[x].siz=w[lc(x)].siz+w[rc(x)].siz+w[x].cnt;
}
inline int chk(int x) { //返回是左孩子还是右孩子,左孩子返回0
return w[w[x].father].ch[1]==x;
}
inline void connect(int x,int fa,int k) { //从fa到x连一条边
w[x].father=fa;
w[fa].ch[k]=x;
}
inline int NewNode(int x,int fa) { //新建一个权值为x,父亲为fa的节点
int id=++cnt;
w[id].cnt=w[id].siz=1;
w[id].val=x;
w[id].father=fa;
return id;
}
旋转
上面说过,不再赘述。
void rotate(int x) {
int y=w[x].father;
int z=w[y].father;
int yson=chk(x),zson=chk(y);
connect(w[x].ch[yson^1],y,yson);
connect(y,x,yson^1);
connect(x,z,zson);
pushup(y);
pushup(x);
}
splay操作(把某个节点不断旋转)
根据实际情况,这里我写的splay是把 x x x旋转到 g o a l goal goal的孩子位置。
void splay(int x,int goal) { //把节点x旋转到goal的孩子的位置
int fa;
while((fa=w[x].father)!=goal) {
if(w[fa].father!=goal) { //x的爷爷不为goal,考虑需不需要双旋
if(chk(x)==chk(fa)) {
rotate(fa);
} else {
rotate(x);
}
}
rotate(x);
}
if(!goal) root=x;
}
删除操作
要删除 x x x,找出 x x x的前驱 l s t lst lst和后继 n x t nxt nxt。
把 l s t lst lst splay到根, n x t nxt nxt splay到 l s t lst lst的(右)孩子处。
根据前驱、后继和二叉搜索树的定义,此时 x x x只可能在 n x t nxt nxt的左子树上,且 n x t nxt nxt的左子树有且仅有 x x x这个节点。
void pop(int x) {
int lst=GetPre(x);
int nxt=GetNxt(x);
splay(lst,0);
splay(nxt,lst); //把nxt接到lst的右孩子上
//此时权值为x的节点只能在nxt的左孩子上
int del=lc(nxt);
if(w[del].cnt>1) {
w[del].cnt--;
splay(del,0);
} else {
w[nxt].ch[0]=0; //如果已经没有x这个节点了,注意删掉
}
}
其他部分不难想到(珂以参考二叉搜索树),其他的题解也讲得很清楚,就不分析了,看后面的代码即可。
P3369完整代码
洛谷P3369 【模板】普通平衡树程序
/*
在太阳西斜的这个世界里,
置身天上之森。
等这场战争结束以后,
不归之人与望眼欲穿的众人,
人人本着正义之名,
长存不灭的过去,逐渐消逝的未来。
我回来了,
纵使日薄西山。
即使看不见未来,
此时此刻的光辉,
盼君勿忘。
——世界上最幸福的女孩
*/
#include
if(w[root].val<x) return root;
int now=w[root].ch[0];
while(w[now].ch[1]) now=w[now].ch[1];
return now;
}
int GetNxt(int x) {
Find(x);
//w[root].val>x,说明没有其他权值更小的节点权值>=x
if(w[root].val>x) return root;
int now=w[root].ch[1];
while(w[now].ch[0]) now=w[now].ch[0];
return now;
}
void pop(int x) {
int lst=GetPre(x);
int nxt=GetNxt(x);
splay(lst,0);
splay(nxt,lst); //把nxt接到lst的右孩子上
//此时权值为x的节点只能在nxt的左孩子上
int del=lc(nxt);
if(w[del].cnt>1) {
w[del].cnt--;
splay(del,0);
} else {
w[nxt].ch[0]=0;
}
}
int main() {
insert(-INF);
insert(INF);
int n=read();
while(n--) {
int op=read();
int x=read();
if(op==1) {
insert(x);
} else if(op==2) {
pop(x);
} else if(op==3) {
Find(x); //Find完后,所有权值小于x的节点都在根节点左子树
printf("%d\n",w[w[root].ch[0]].siz); //有一个-INF,所以不用+1
} else if(op==4) {
printf("%d\n",kth(x+1)); //有一个-INF,所以要+1
} else if(op==5) {
printf("%d\n",w[GetPre(x)].val);
} else {
printf("%d\n",w[GetNxt(x)].val);
}
}
return 0;
}
/*
10
1 5
1 6
1 7
*/
区间反转操作(洛谷P3391 文艺平衡树)
题目链接
要解决这道题,先证明几个引理:
引理1:中序遍历二叉搜索树,权值从小到大排序。
证明:中序遍历是左子树->根->右子树,而二叉搜索树满足左<根<右的性质。
所以遍历出的所有权值中,若两个权值相邻,则必有先遍历出的权值<后遍历出的权值。
引理2:在rotate操作后,中序遍历的顺序不变
证明:把左旋、右旋的图画出来,发现旋转不会改变中序遍历顺序。
以上面讲旋转操作部分的左旋图为例。

中序遍历:XBYAC。

中序遍历:XBYAC。
右旋同理。
引理3:假设 [ l , r ] [l,r] [l,r]区间内的所有节点都在同一棵子树内。交换这棵子树的所有节点的左右孩子,可以让中序遍历时 [ l , r ] [l,r] [l,r]这一段区间反转。
证明:
原来中序遍历的顺序中,若 x x x比 y y y先遍历到,那么一定会在 L C A ( x , y ) LCA(x,y) LCA(x,y)处 x x x在左子树, y y y在右子树(由LCA的定义易知)。
反转之后,因为左右子树反转,所以 x x x被换到了 L C A ( x , y ) LCA(x,y) LCA(x,y)的右子树, y y y到了 L C A ( x , y ) LCA(x,y) LCA(x,y)的左子树。
因此在交换左右子树之后, x x x比 y y y后遍历。
这道题反转 [ l , r ] [l,r] [l,r]区间相当于反转中序遍历第 l l l个到第 r r r个。
由引理3,我们要反转 [ l , r ] [l,r] [l,r]时,先把 [ l , r ] [l,r] [l,r]通过某种方式弄到同一个子树内,然后打区间反转标记,然后在需要时下传标记即珂qwq。
把 [ l , r ] [l,r] [l,r]弄到同一个子树珂以把中序遍历第 l − 1 l-1 l−1个splay到根,再把中序遍历第 r + 1 r+1 r+1个splay到第 l − 1 l-1 l−1个的子树。
根据中序遍历的定义,中序遍历 [ l , r ] [l,r] [l,r]就在此时中序遍历第 r + 1 r+1 r+1个的左子树。这样就让 [ l , r ] [l,r] [l,r]都在同一棵子树中了qwq。
具体实现时,因为插入了-INF和+INF,所以要注意边界。
这道题中,由于要交换左右子树,所以交换后的splay tree的权值会不符合二叉搜索树性质,所以大胆猜测有区间反转就不能查询排名等信息(欢迎打脸)
P3391代码
#include