平稳时间序列参数估计
说明
对未知参数的估计方法有三种:矩估计(运用p+q个样本的自相关系数估计总体的自相关系数),极大似然估计(使得联合密度函数达到最大的参数值),最小二乘估计(使得残差平方和达到最小的那组参数值即为最小二乘估计)。
在R语言中,参数估计通过调用ARIMA函数来完成,该函数的命令格式为:
arima(x,order=,include.mean=,method=)
-x:要进行模型拟合的序列名.
-order:指定模型阶数.order = c(p,d,q)
(1)p阶自回归函数.
(2)d为差分阶数.
(3)q为移动平均阶数.
-include.mean:要不要包括常数项.
(1)include.mean = T,需要拟合常数项,这也是系统默设置。
(2)include.mean = F,不拟合常数项.
-method:指定参数估计:指定参数估计方法.
(1)method = “CSS-ML”,默认的是条件最小二乘与极大似然估计混合方法.
(2)method = “CSS-ML”,极大似然估计.
(3)method = “CSS”,条件最小二乘估计.
AR(2)拟合模型的口径
1950-2008年我国邮路及农村投递线路每年新增里程数.
x<-ts(a$kilometer,start=1950)
x.fit<-arima(x,order = c(2,0,0),method = "ML")
x.fit
Call:
arima(x = x, order = c(2, 0, 0), method = "ML")
Coefficients:
ar1 ar2 intercept
0.7185 -0.5294 11.0223
s.e. 0.1083 0.1067 3.0906
sigma^2 estimated as 365.2: log likelihood = -258.23, aic = 524.46MA(1)拟合模型的口径
某个加油站连续57天的overshort
overshort<-ts(overshort$overshort)
> overshort.fit<-arima(overshort,order = c(0,0,1))
> overshort.fit
Call:
arima(x = overshort, order = c(0, 0, 1))
Coefficients:
ma1 intercept
-0.8477 -4.7945
s.e. 0.1206 1.0252
sigma^2 estimated as 2020: log likelihood = -298.42, aic = 602.84arma(1,1)拟合模型的口径
dif_x<-ts(diff(b$change_temp),start = 1880)
> dif_x.fit<-arima(dif_x,order = c(1,0,1))
> dif_x.fit
Call:
arima(x = dif_x, order = c(1, 0, 1))
Coefficients:
ar1 ma1 intercept
0.3926 -0.8867 0.0053
s.e. 0.1180 0.0604 0.0024
sigma^2 estimated as 0.01541: log likelihood = 69.66, aic = -131.32模型检验
确定拟合模型的口径之后,我们还要对该模型进行必要的检验。
模型的显著性检验
模型的显著性检验主要是检验模型的有效性,一个模型是否显著有效主要看它提取的信息是否充分,一个好的拟合模型应该能够提取观察值序列中几乎所有的样本相关信息,换言之,拟合残差项中将不再蕴含任何的相关信息,即残差序列应该为白噪声序列,这样的模型应该为显著有效模型。
显示性检测AR(2)
1950-2008年我国邮路及农村投递线路每年新增里程数序列
x<-ts(a$kilometer,start=1950)
> x.fit<-arima(x,order = c(2,0,0),method = "ML")
> for(i in 1:2) print(Box.test(x.fit$residual,lag=6*i))
Box-Pierce test
data: x.fit$residual
X-squared = 2.0949, df = 6, p-value = 0.9108
Box-Pierce test
data: x.fit$residual
X-squared = 2.8341, df = 12, p-value = 0.9966由于各阶延迟下LB统计量的p值都显著大于0.05,可以认为这个拟合模型的残差序列属于白噪序列,即该拟合模型显著有效。
显示性检测MA(1)
某个加油站连续57天的overshort
overshort<-ts(overshort$overshort)
overshort.fit<-arima(overshort,order = c(0,0,1))
for(i in 1:2) print(Box.test(overshort.fit$residual,lag=6*i))
Box-Pierce test
data: overshort.fit$residual
X-squared = 2.984, df = 6, p-value = 0.8108
Box-Pierce test
data: overshort.fit$residual
X-squared = 8.4545, df = 12, p-value = 0.7487
显示性检测ARMA(1,1)
1880-1985年全球气表平均温度改变值差分序列
> dif_x<-ts(diff(b$change_temp),start = 1880)
> dif_x.fit<-arima(dif_x,order = c(1,0,1),method = "CSS")
> for(i in 1:2) print(Box.test(dif_x.fit$residual,lag=6*i))
Box-Pierce test
data: dif_x.fit$residual
X-squared = 4.593, df = 6, p-value = 0.597
Box-Pierce test
data: dif_x.fit$residual
X-squared = 9.1007, df = 12, p-value = 0.6943残差检验结果显示,残差序列可视为白噪声序列,这说明拟合模型ARMA(1,1)显著有效。
参数的显著性检验
参数的显著性检验就是要检验每一个未知参数是否显著非零,这个检验是使模型最精简。
如果某个参数不显著,即表示该参数所对应的那个自变量对因变量的影响不明显,该自变量可以从拟合模型中剔除,最终模型将由一系列参数显著非零的自变量表示。
R不提供参数的显著性检验结果,一般默认输出参数均显著非零,如果用户想获取参数检验统计的p值,需要自己计算参数的t统计量的值以及统计量的p值。
调用t分布p函数pt即可获得统计量的p值,pt函数的命令格式为:
pt(t ,df= ,low.tail= )
-t:统计量的值
-df:自由度。
-lower.tail:确定计算概率的方向
(1)lower.tail = T,计算Pr(X<=x).对于参数显著性检验,如果参数估计值为负,选择lower.tail=T.
(2)lower.tail = F,计算Pr(X>x).对于参数显著性检验,如果参数估计值为正,选择lower.tail=F.
AR(2)拟合模型参数的显著性
1950-2008年我国邮路及农村投递线路每年新增里程数序列
> x<-ts(a$kilometer,start=1950)
> x.fit<-arima(x,order = c(2,0,0),method = "ML")
> x.fit
Call:
arima(x = x, order = c(2, 0, 0), method = "ML")
Coefficients:
ar1 ar2 intercept
0.7185 -0.5294 11.0223
s.e. 0.1083 0.1067 3.0906
sigma^2 estimated as 365.2: log likelihood = -258.23, aic = 524.46
> #ar1系数显著性检验
> t1<-0.7185/0.1083
> pt(t1,df=56,lower.tail = F)
[1] 6.94276e-09
> #ar2系数显著性检验
> t2<-0.5294/0.1067
> pt(t2,df=56,lower.tail = T)
[1] 0.9999966
> #ar3系数显著性检验
> t0=11.0223/3.0906
> pt(t0,df=56,lower.tail = F)
[1] 0.0003748601检验结果显示,三个系数均显著非零。
模型优化
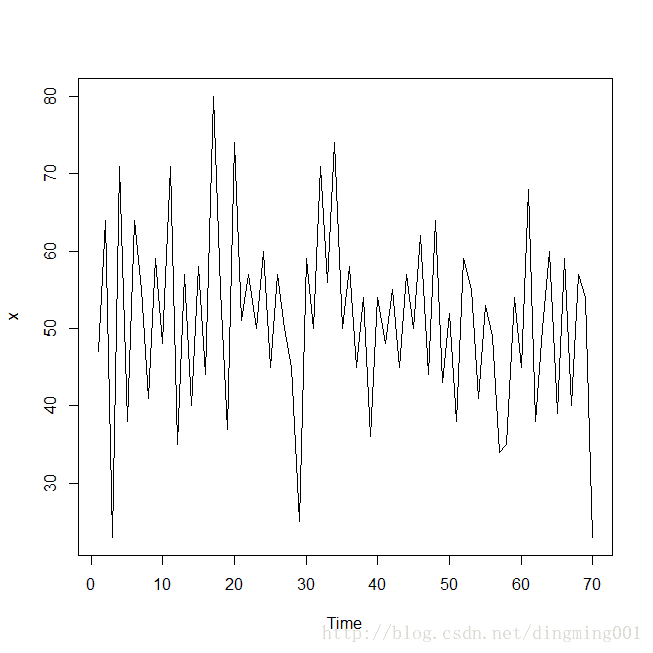
若一个模型通过了检测,说明在一定的置信水平下,该模型能够有效的拟合观察值序列的波动,但这种有效模型并不是唯一。等时间间隔,连续取某次化学反应的70个过程数据,构成一个时序列表。
x<-ts(x$yield)
plot(x)for(i in 1:2) print(Box.test(x,lag=6*i))
Box-Pierce test
data: x
X-squared = 20.209, df = 6, p-value = 0.002542
Box-Pierce test
data: x
X-squared = 21.622, df = 12, p-value = 0.04198绘制自相关图和偏自相关图
acf(x)
pacf(x)> x.fit1<-arima(x,order = c(0,0,2))
> x.fit1
Call:
arima(x = x, order = c(0, 0, 2))
Coefficients:
ma1 ma2 intercept
-0.3194 0.3019 51.1695
s.e. 0.1160 0.1233 1.2516
sigma^2 estimated as 114.4: log likelihood = -265.35, aic = 538.71MA(2)模型显著性检验
for(i in 1:2) print(Box.test(x.fit1$residual,lag=6*i))
Box-Pierce test
data: x.fit1$residual
X-squared = 2.1105, df = 6, p-value = 0.9093
Box-Pierce test
data: x.fit1$residual
X-squared = 3.9217, df = 12, p-value = 0.9848拟合AR(1)模型
x.fit2<-arima(x,order = c(1,0,0))
> x.fit2
Call:
arima(x = x, order = c(1, 0, 0))
Coefficients:
ar1 intercept
-0.4191 51.2658
s.e. 0.1129 0.9137
sigma^2 estimated as 116.6: log likelihood = -265.98, aic = 537.96
#AR(1)模型显著性检验
for(i in 1:2) print(Box.test(x.fit2$residual,lag=6*i))
Box-Pierce test
data: x.fit2$residual
X-squared = 4.1678, df = 6, p-value = 0.654
Box-Pierce test
data: x.fit2$residual
X-squared = 6.1411, df = 12, p-value = 0.9088观测可以得知,同一个序列可以构造两个序列模型,两个模型都显著有效,对于如何选择问题,可以引进AIC和SBC(BIC)信息准则的概念进行模型优化。
AIC准则
最小信息量准则,指导思想是拟合模型的优劣可以可以从两个方面进行考虑:一个是衡量拟合程序的似然函数值,模型中未知参数的个数。
但是未知参数越多,说明模型中自变量越多,未知的风险越多,而且参数越多,参数估计的难度就越大,估计的精度也就越差。所以一个好的拟合模型应该是拟合精度和未知参数的个数的综合最优配置。
AIC函数达到最小的模型被认为是最优模型。
另外一种模型
SBC(BIC)准则
AIC模型也有一些不足之处,对于一个观察值序列而言,序列越长,相关信息就越分散,要充分的提取其中的有用信息,或者使拟合精度比较高,通常要包括多个自变量的复杂模型。在AIC准则中拟合误差提供的信息要受到样本容量的放大,而参数个数的惩罚因子却和样本容量没有关系,它的权重始终是不变。
因此当样本无穷大时,由AIC准则选择的模型不收敛于真实模型,它通常比真实模型所含有的未知个数要多。
SBC对AIC的改进就是就是将未知参数个数惩罚权重由常数变成样本容量的对数函数,理论上,SBC的准则确定的最优模型是真实阶数的相合估计。
通过对上例中参数对比:
模型 AIC SBC
MA(2) 538.71 547.7
AR(1) 537.96 544.7
从两个方面比较,AR(1)都要优于MA(2),AIC准则与SBC准则的提出,可以有效的弥补自相关图与偏自相关图定阶的主观性,在有限有阶数范围内帮助我们找到最优拟合模型。