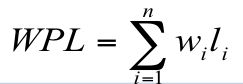- C#中使用split分割字符串
互联网打工人no1
c#
1、用字符串分隔:usingSystem.Text.RegularExpressions;stringstr="aaajsbbbjsccc";string[]sArray=Regex.Split(str,"js",RegexOptions.IgnoreCase);foreach(stringiinsArray)Response.Write(i.ToString()+"");输出结果:aaabbbc
- 你可能遗漏的一些C#/.NET/.NET Core知识点
追逐时光者
C#.NETDotNetGuide编程指南c#.net.netcoremicrosoft
前言在这个快速发展的技术世界中,时常会有一些重要的知识点、信息或细节被忽略或遗漏。《C#/.NET/.NETCore拾遗补漏》专栏我们将探讨一些可能被忽略或遗漏的重要知识点、信息或细节,以帮助大家更全面地了解这些技术栈的特性和发展方向。拾遗补漏GitHub开源地址https://github.com/YSGStudyHards/DotNetGuide/blob/main/docs/DotNet/D
- C#动态加载DLL程序集及使用反射创建实例-简记
不全
C#相关Asp.netWebFormAsp.netMVCc#Assembly反射程序集
Assembly动态加载程序集:分两种情况:1、需要加载的程序集已经在程序中被引用了,则直接从当前程序域中查找即可:Assemblyassembly=AppDomain.CurrentDomain.GetAssemblies().FirstOrDefault(x=>x.GetName().Name.Contains("theAssemblyName"));2、需要加载的程序集未被加载,则使用程序集
- 开发游戏的学习规划
杰克逊的日记
游戏学习
第一阶段:●C#语言快速系统地学习一遍(基础的语法、面向对象、基础的数据结构、基础的设计模式)●Unity的2D和3D部分及UI、动画、物理系统●阶段性测验:需要去用前面所学的这些基础知识来完成一个简单的2d或者3d的案例,将通过一个自制的《Flappybird》游戏案例讲解游戏开发的思想及方法,并将《Flappybird》这个游戏进一步改造成一个横版射击类游戏《Crazybird》以巩固并且升华
- python可以制作大型游戏_python能做游戏吗-python能开发游戏吗
靖dede
python可以制作大型游戏
python可以写游戏,但不适合。下面我们来分析一下具体原因。用锤子能造汽车吗?谁也没法说不能吧?历史上也确实曾经有些汽车,是用锤子造出来的。但一般来说,还是用工业机器人更合适对吗?比较大型的,使用Python的游戏有两个,一个是《EVE》,还有一个是《文明》。但这仅仅是个例,没有广泛意义。一般来说,用来做游戏的语言,有两种。一是C++。。一是C#。。Python理论上,不仅不适合做游戏,而是只要
- 【C#生态园】深度剖析:C#嵌入式开发工具大揭秘
friklogff
C#生态园c#开发语言
C#嵌入式开发:全面了解六大框架与库前言随着物联网和嵌入式系统的快速发展,越来越多的开发者开始关注使用C#语言进行嵌入式开发。本文将介绍几种用于C#的嵌入式开发框架和相关库,以及它们的核心功能、安装配置方法和API概览,帮助读者了解并选择适合自己项目的工具和资源。欢迎订阅专栏:C#生态园文章目录C#嵌入式开发:全面了解六大框架与库前言1.nanoFramework:一个用于C#的嵌入式开发框架1.
- Lua 与 C#交互
z2014z
luac#开发语言
Lua与C#交互前提Lua是一种嵌入式脚本语言,Lua的解释器是用C编写的,因此可以方便的与C/C++进行相互调用。轻量级Lua语言的官方版本只包括一个精简的核心和最基本的库,这使得Lua体积小、启动速度快,也适合嵌入在别的程序里。交互过程C#调用Lua:由C#文件调用Lua解析器底层dll库(由C语言编写),再由dll文件执行相应的Lua文件。Lua调用C#:1、Wrap方式:首先生成C#源文件
- C# 开发教程-入门基础
天马3798
教程系列整理c#开发语言
1.C#简介、环境,程序结构2.C#基本语法,变量,控制局域,数据类型,类型转换3.C#数组、循环,Linq4.C#类,封装,方法5.C#枚举、字符串6.C#面相对象,继承,封装,多态7.C#特性、属性、反射、索引器8.C#委托,事件,集合,泛型9.C#匿名方法10.C#多线程更多:JQuery开发教程入门基础Vue开发基础入门教程Vue开发高级学习教程
- C# 禁止程序重复启动
wiseyao1219
c#
修改:Program.cs[STAThread]staticvoidMain(){Mutexmutex=newMutex(true,"NewGuid123456",outboolisCreatedNew);if(!isCreatedNew){MessageBox.Show(Application.ProductName+"isrunning...");return;}Application.Ena
- C#中判断socket是否已断开的方法
wiseyao1219
c#
代码如下:Sockets=newSocket(..);if(s.Poll(-1,SelectMode.SelectRead)){intnRead=s.Receive();if(nRead==0){//socket连接已断开}}参考:C#中判断socket是否已断开的方法
- C#文件被占用的解决方案
花北城
C#项目文件占用
问题打更新包时,提示文件被占用。System.IO.IOException:文件“D:\RS\RS_CCVI20111210.exe”正由另一进程使用,因此该进程无法访问该文件。在System.IO.__Error.WinIOError(Int32errorCode,StringmaybeFullPath)在System.IO.FileStream.Init(Stringpath,FileMode
- C#实现软件自动升级
BruceEditCode
winform程序相对web程序而言,功能更强大,编程更方便,但软件更新却相当麻烦,要到客户端一台一台地升级,本文结合实际情况,通过软件实现自动升级,弥补了这一缺陷,有较好的参考价值。由于程序在运行时不能用新的版本覆盖自己,因此,我们将登录窗口单独做成一个可执行文件,用户登录时,从网上检测是否有新的主程序,如果有,则从后台下载并覆盖老的版本,用户输入正确的用户名和密码后,通过参数将必要的信息(如用
- C# 自动化
TineAine
C#代码片段自动化c#自动化模拟操作
实现的方法可能很笨,但是确实很好用usingSystem;usingSystem.Collections.Generic;usingSystem.Linq;usingSystem.Runtime.InteropServices;usingSystem.Text;usingSystem.Threading;usingSystem.Threading.Tasks;/******************
- 技术周总结 09.09~09.15周日(C# WinForm WPF)
打破砂锅问到底007
wpfc#WinForm
文章目录一、09.09周一1.1)问题01:Windows桌面开发中,WPF和WinForm的区别和联系?联系:区别:二、09.12周四2.1)问题01:visualstudio的相关快捷键有哪些?通用快捷键编辑导航调试窗口管理2.2)问题02:publicpartialclassChoosePLReason:CommonBaseForm2.3)问题03:介绍WindowsForms中的Syste
- 通过C# 裁剪PDF页面
Eiceblue
C#.NETPDFc#pdf开发语言visualstudio
在处理PDF文档时,有时需要精确地裁剪页面以适应特定需求,比如去除广告、背景信息或者仅仅是为了简化文档内容。本文将指导如何使用免费.NET控件通过C#实现裁剪PDF页面。免费库FreeSpire.PDFfor.NET支持在.NET(C#,VB.NET,ASP.NET,.NETCore)程序中实现创建、操作、转换和打印PDF文档等操作。可以从以下链接下载产品包后手动添加引用,或者直接通过NuGet安
- 【Unity基础】如何选择脚本编译方式Mono和IL2CPP?
tealcwu
Unity基础unity游戏引擎
Edit->ProjectSettings->Player在Unity中,ScriptingBackend决定了项目的脚本编译方式,即如何将C#代码转换为可执行代码。Unity提供了两种主要的ScriptingBackend选项:Mono和IL2CPP。它们之间的区别影响了项目的性能、平台支持、编译时间和调试体验。以下是两者的详细对比:1.Mono简介:Mono是Unity最早使用的脚本后端,基于
- C# Tuple、ValueTuple
語衣
C#知识补充c#
栏目总目录TupleTuple是C#4.0引入的一个新特性,主要用于存储一个固定数量的元素序列,且这些元素可以具有不同的类型。Tuple是一种轻量级的数据结构,非常适合用于临时存储数据,而无需定义完整的类或结构体。优点简便性:可以快速创建一个包含多个不同类型数据的对象,而无需定义新的类或结构体。灵活性:元素数量和类型在编译时确定,但可以在不同上下文中重复使用不同元素的Tuple。缺点性能:作为引用
- C# Linq语句用法大全以及Lambda表达式
一个小码码
c#linq开发语言.net
C#Linq语句用法大全以及Lambda表达式Linq:是一种用于数据查询和操作的语言集成查询(LanguageIntegratedQuery)技术。通过Linq,我们可以使用类似于SQL查询的方式来查询、筛选和操作各种类型的数据集合,包括数组、列表、集合、XML文档、数据库表等等。常见的有:LinqtoObjects:用于操作对象集合,例如数组、列表等。LinqtoXML:用于操作XML数据,支
- C#中的LInq语句
weixin_30588907
c#数据库
语言集成查询(LINQ)是一组技术的名称,这些技术建立在将查询功能直接集成到C#语言(以及VisualBasic和可能的任何其他.NET语言)的基础上。借助于LINQ,查询现在已是高级语言构造,就如同类、方法、事件等等。对于编写查询的开发人员来说,LINQ最明显的“语言集成”部分是查询表达式。查询表达式是使用C#3.0中引入的声明性查询语法编写的。通过使用查询语法,您甚至可以使用最少的代码对数据源
- C#的linq语句
木生火18624
C#开发
/查询表达式必须以form子句开头,以select或者group子句结束,在这两个子句之间,可以使用///where、orderby、join、let和其他的from子句本章要点用列表在对象上执行传统查询扩展方法LINQ查询操作符平行LNQ表达式树本章源代码下载地址(wrox.com)打开网页www.wrox.com/go/procsharp,单击DownloadCode选项卡即可下载本章源代码。
- C# 多线程操作同一个文件,如何避免冲突
FlYFlOWERANDLEAF
c#开发语言
1使用lock经测试,依然存在线程冲突privatestaticobjectlocker=newobject();……lock(locker){stringbText=File.ReadAllText(FPath);returnbText;}……lock(locker){File.WriteAllText(FPath,aContent);}2使用ReaderWriterLockSlim经测试,依然
- C#LINQ常用扩展语句
月落.
C#c#linqsolr
在C#中,LINQ提供了许多扩展方法,这些方法定义在System.Linq命名空间中。以下是一些常用的LINQ扩展方法:Where-过滤数据集合,返回满足条件的元素。varfilteredItems=collection.Where(item=>item.SomeProperty>10);Select-从数据集合中选择数据或创建新的投影。varprojectedItems=collection.S
- source insight4.0中文乱码解决方法
鹿屿二向箔
c语言stm32keilmdk
Sourceinsight是强大、顺手的代码编辑器,它几乎支持所有的语言,包括:C,C++,C#,HTML等等,能够自动创建并维护它自己高性能的符号数据库,包括函数、全局变量、结构、类和工程源文件里定义的其它类型的符号,对于大工程的源码阅读非常方便。但是因为是国外软件,对中文支持不是很好,很多电脑安装使用都会出现注释乱码问题,很让人抓狂。网上很多人遇到类似的问题,也有很多解决方式,也有很多“终极解
- C#基础知识-.NET,变量,容量单位,数据类型
yi碗汤园
c#开发语言
目录1.NET简介2.变量1)定义2)声明3)赋值3.容量单位4.数据类型1)整形(整数)2)非整型(小数)3)非数值型本篇文章来分享一下C#的基础知识,主要讲述一下变量和数据类型的相关知识。1.NET简介.NETdonet是Microsoft新一代多语言的开发平台,用于构建和运行应用程序。Unity借助Mono实现跨平台,核心是.NETFramework框架。2.变量1)什么是变量变量是用来存储
- C# 在WPF中实现图表生成
A_nanda
WPF赏析c#wpf开发语言
在现代应用程序中,数据可视化是一个重要的功能,它可以帮助用户更直观地理解数据。在C#WPF(WindowsPresentationFoundation)中,有多种方式可以生成图表。以下是五种常见的方法,每种方法都有其独特的优势和局限。1.使用System.Windows.Shapes命名空间代码示例:<RectangleWidth="50"Height="50"Fill="Blue"Canva
- C#中关闭窗口清除内容
Vae_Mars
AI对话中的其他知识c#开发语言
1.解释说明-窗口关闭时是可以执行函数的,可以做一部分事件处理-因为删除文件夹的方案不好做,所以改成清空文件夹内的内容2.程序示例publicMainWindow(){InitializeComponent();//检查窗口关闭this.Closing+=MainWindow_Closing;}//执行具体的方法privatevoidMainWindow_Closing(objectsender,
- C#中Invoke的用法()
世界太过浮夸
.netc#
转自:http://www.cnblogs.com/lsgsanxiao/p/5523282.htmlinvoke和begininvoke区别一直对invoke和begininvoke的使用和概念比较混乱,这两天看了些资料,对这两个的用法和原理有了些新的认识和理解。首先说下,invoke和begininvoke的使用有两种情况:control中的invoke、begininvoke。delegra
- .NET常见面试题汇总
.Net Core 爱好者
.netc#
首先,汇总一共分为三部分:一是关于.NET技术的面试问题,二是关于.NET项目中的实际问题,三是历年出现过一些面试题汇总一、.NET技术面试问题请简述.NET中的装箱和拆箱。什么是泛型,以及它在.NET中的用途?请解释一下C#中的委托是什么,以及它们如何工作?什么是事件,如何使用它们?请解释一下C#中的特性(Attributes)及其应用场景。.NET中的异步编程模式有哪些?什么是LINQ,它在.
- c# net8调用vc写的dll
wiseyao1219
c#开发语言dll
dll程序(vc,x86)头文件extern"C"int__declspec(dllexport)WINAPIadd(inta,intb);实现intWINAPIadd(inta,intb){returna+b;}c#/net8函数声明:[DllImport("dll/Dll1.dll",CallingConvention=CallingConvention.StdCall)]publicstat
- c# json使用
wiseyao1219
c#json前端
安装包用NuGet安装包:Newtonsoft.Json对象转为Json字符串publicclassPerson{publicstringName{get;set;}publicintAge{get;set;}}Personperson=newPerson{Name="JohnDoe",Age=30};stringjson2=JsonConvert.SerializeObject(person);
- 解读Servlet原理篇二---GenericServlet与HttpServlet
周凡杨
javaHttpServlet源理GenericService源码
在上一篇《解读Servlet原理篇一》中提到,要实现javax.servlet.Servlet接口(即写自己的Servlet应用),你可以写一个继承自javax.servlet.GenericServletr的generic Servlet ,也可以写一个继承自java.servlet.http.HttpServlet的HTTP Servlet(这就是为什么我们自定义的Servlet通常是exte
- MySQL性能优化
bijian1013
数据库mysql
性能优化是通过某些有效的方法来提高MySQL的运行速度,减少占用的磁盘空间。性能优化包含很多方面,例如优化查询速度,优化更新速度和优化MySQL服务器等。本文介绍方法的主要有:
a.优化查询
b.优化数据库结构
- ThreadPool定时重试
dai_lm
javaThreadPoolthreadtimertimertask
项目需要当某事件触发时,执行http请求任务,失败时需要有重试机制,并根据失败次数的增加,重试间隔也相应增加,任务可能并发。
由于是耗时任务,首先考虑的就是用线程来实现,并且为了节约资源,因而选择线程池。
为了解决不定间隔的重试,选择Timer和TimerTask来完成
package threadpool;
public class ThreadPoolTest {
- Oracle 查看数据库的连接情况
周凡杨
sqloracle 连接
首先要说的是,不同版本数据库提供的系统表会有不同,你可以根据数据字典查看该版本数据库所提供的表。
select * from dict where table_name like '%SESSION%';
就可以查出一些表,然后根据这些表就可以获得会话信息
select sid,serial#,status,username,schemaname,osuser,terminal,ma
- 类的继承
朱辉辉33
java
类的继承可以提高代码的重用行,减少冗余代码;还能提高代码的扩展性。Java继承的关键字是extends
格式:public class 类名(子类)extends 类名(父类){ }
子类可以继承到父类所有的属性和普通方法,但不能继承构造方法。且子类可以直接使用父类的public和
protected属性,但要使用private属性仍需通过调用。
子类的方法可以重写,但必须和父类的返回值类
- android 悬浮窗特效
肆无忌惮_
android
最近在开发项目的时候需要做一个悬浮层的动画,类似于支付宝掉钱动画。但是区别在于,需求是浮出一个窗口,之后边缩放边位移至屏幕右下角标签处。效果图如下:
一开始考虑用自定义View来做。后来发现开线程让其移动很卡,ListView+动画也没法精确定位到目标点。
后来想利用Dialog的dismiss动画来完成。
自定义一个Dialog后,在styl
- hadoop伪分布式搭建
林鹤霄
hadoop
要修改4个文件 1: vim hadoop-env.sh 第九行 2: vim core-site.xml <configuration> &n
- gdb调试命令
aigo
gdb
原文:http://blog.csdn.net/hanchaoman/article/details/5517362
一、GDB常用命令简介
r run 运行.程序还没有运行前使用 c cuntinue
- Socket编程的HelloWorld实例
alleni123
socket
public class Client
{
public static void main(String[] args)
{
Client c=new Client();
c.receiveMessage();
}
public void receiveMessage(){
Socket s=null;
BufferedRea
- 线程同步和异步
百合不是茶
线程同步异步
多线程和同步 : 如进程、线程同步,可理解为进程或线程A和B一块配合,A执行到一定程度时要依靠B的某个结果,于是停下来,示意B运行;B依言执行,再将结果给A;A再继续操作。 所谓同步,就是在发出一个功能调用时,在没有得到结果之前,该调用就不返回,同时其它线程也不能调用这个方法
多线程和异步:多线程可以做不同的事情,涉及到线程通知
&
- JSP中文乱码分析
bijian1013
javajsp中文乱码
在JSP的开发过程中,经常出现中文乱码的问题。
首先了解一下Java中文问题的由来:
Java的内核和class文件是基于unicode的,这使Java程序具有良好的跨平台性,但也带来了一些中文乱码问题的麻烦。原因主要有两方面,
- js实现页面跳转重定向的几种方式
bijian1013
JavaScript重定向
js实现页面跳转重定向有如下几种方式:
一.window.location.href
<script language="javascript"type="text/javascript">
window.location.href="http://www.baidu.c
- 【Struts2三】Struts2 Action转发类型
bit1129
struts2
在【Struts2一】 Struts Hello World http://bit1129.iteye.com/blog/2109365中配置了一个简单的Action,配置如下
<!DOCTYPE struts PUBLIC
"-//Apache Software Foundation//DTD Struts Configurat
- 【HBase十一】Java API操作HBase
bit1129
hbase
Admin类的主要方法注释:
1. 创建表
/**
* Creates a new table. Synchronous operation.
*
* @param desc table descriptor for table
* @throws IllegalArgumentException if the table name is res
- nginx gzip
ronin47
nginx gzip
Nginx GZip 压缩
Nginx GZip 模块文档详见:http://wiki.nginx.org/HttpGzipModule
常用配置片段如下:
gzip on; gzip_comp_level 2; # 压缩比例,比例越大,压缩时间越长。默认是1 gzip_types text/css text/javascript; # 哪些文件可以被压缩 gzip_disable &q
- java-7.微软亚院之编程判断俩个链表是否相交 给出俩个单向链表的头指针,比如 h1 , h2 ,判断这俩个链表是否相交
bylijinnan
java
public class LinkListTest {
/**
* we deal with two main missions:
*
* A.
* 1.we create two joined-List(both have no loop)
* 2.whether list1 and list2 join
* 3.print the join
- Spring源码学习-JdbcTemplate batchUpdate批量操作
bylijinnan
javaspring
Spring JdbcTemplate的batch操作最后还是利用了JDBC提供的方法,Spring只是做了一下改造和封装
JDBC的batch操作:
String sql = "INSERT INTO CUSTOMER " +
"(CUST_ID, NAME, AGE) VALUES (?, ?, ?)";
- [JWFD开源工作流]大规模拓扑矩阵存储结构最新进展
comsci
工作流
生成和创建类已经完成,构造一个100万个元素的矩阵模型,存储空间只有11M大,请大家参考我在博客园上面的文档"构造下一代工作流存储结构的尝试",更加相信的设计和代码将陆续推出.........
竞争对手的能力也很强.......,我相信..你们一定能够先于我们推出大规模拓扑扫描和分析系统的....
- base64编码和url编码
cuityang
base64url
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.PrintWriter;
import java.io.StringWriter;
import java.io.UnsupportedEncodingException;
- web应用集群Session保持
dalan_123
session
关于使用 memcached 或redis 存储 session ,以及使用 terracotta 服务器共享。建议使用 redis,不仅仅因为它可以将缓存的内容持久化,还因为它支持的单个对象比较大,而且数据类型丰富,不只是缓存 session,还可以做其他用途,一举几得啊。1、使用 filter 方法存储这种方法比较推荐,因为它的服务器使用范围比较多,不仅限于tomcat ,而且实现的原理比较简
- Yii 框架里数据库操作详解-[增加、查询、更新、删除的方法 'AR模式']
dcj3sjt126com
数据库
public function getMinLimit () { $sql = "..."; $result = yii::app()->db->createCo
- solr StatsComponent(聚合统计)
eksliang
solr聚合查询solr stats
StatsComponent
转载请出自出处:http://eksliang.iteye.com/blog/2169134
http://eksliang.iteye.com/ 一、概述
Solr可以利用StatsComponent 实现数据库的聚合统计查询,也就是min、max、avg、count、sum的功能
二、参数
- 百度一道面试题
greemranqq
位运算百度面试寻找奇数算法bitmap 算法
那天看朋友提了一个百度面试的题目:怎么找出{1,1,2,3,3,4,4,4,5,5,5,5} 找出出现次数为奇数的数字.
我这里复制的是原话,当然顺序是不一定的,很多拿到题目第一反应就是用map,当然可以解决,但是效率不高。
还有人觉得应该用算法xxx,我是没想到用啥算法好...!
还有觉得应该先排序...
还有觉
- Spring之在开发中使用SpringJDBC
ihuning
spring
在实际开发中使用SpringJDBC有两种方式:
1. 在Dao中添加属性JdbcTemplate并用Spring注入;
JdbcTemplate类被设计成为线程安全的,所以可以在IOC 容器中声明它的单个实例,并将这个实例注入到所有的 DAO 实例中。JdbcTemplate也利用了Java 1.5 的特定(自动装箱,泛型,可变长度
- JSON API 1.0 核心开发者自述 | 你所不知道的那些技术细节
justjavac
json
2013年5月,Yehuda Katz 完成了JSON API(英文,中文) 技术规范的初稿。事情就发生在 RailsConf 之后,在那次会议上他和 Steve Klabnik 就 JSON 雏形的技术细节相聊甚欢。在沟通单一 Rails 服务器库—— ActiveModel::Serializers 和单一 JavaScript 客户端库——&
- 网站项目建设流程概述
macroli
工作
一.概念
网站项目管理就是根据特定的规范、在预算范围内、按时完成的网站开发任务。
二.需求分析
项目立项
我们接到客户的业务咨询,经过双方不断的接洽和了解,并通过基本的可行性讨论够,初步达成制作协议,这时就需要将项目立项。较好的做法是成立一个专门的项目小组,小组成员包括:项目经理,网页设计,程序员,测试员,编辑/文档等必须人员。项目实行项目经理制。
客户的需求说明书
第一步是需
- AngularJs 三目运算 表达式判断
qiaolevip
每天进步一点点学习永无止境众观千象AngularJS
事件回顾:由于需要修改同一个模板,里面包含2个不同的内容,第一个里面使用的时间差和第二个里面名称不一样,其他过滤器,内容都大同小异。希望杜绝If这样比较傻的来判断if-show or not,继续追究其源码。
var b = "{{",
a = "}}";
this.startSymbol = function(a) {
- Spark算子:统计RDD分区中的元素及数量
superlxw1234
sparkspark算子Spark RDD分区元素
关键字:Spark算子、Spark RDD分区、Spark RDD分区元素数量
Spark RDD是被分区的,在生成RDD时候,一般可以指定分区的数量,如果不指定分区数量,当RDD从集合创建时候,则默认为该程序所分配到的资源的CPU核数,如果是从HDFS文件创建,默认为文件的Block数。
可以利用RDD的mapPartitionsWithInd
- Spring 3.2.x将于2016年12月31日停止支持
wiselyman
Spring 3
Spring 团队公布在2016年12月31日停止对Spring Framework 3.2.x(包含tomcat 6.x)的支持。在此之前spring团队将持续发布3.2.x的维护版本。
请大家及时准备及时升级到Spring
- fis纯前端解决方案fis-pure
zccst
JavaScript
作者:zccst
FIS通过插件扩展可以完美的支持模块化的前端开发方案,我们通过FIS的二次封装能力,封装了一个功能完备的纯前端模块化方案pure。
1,fis-pure的安装
$ fis install -g fis-pure
$ pure -v
0.1.4
2,下载demo到本地
git clone https://github.com/hefangshi/f