非参数统计概述
非参数统计概述
文章目录
- 非参数统计概述
- 引言
- 非参数方法举例
- Wilcoxon 符号秩检验
- Wilcoxon秩和检验
- 斯皮尔曼相关性检验
- Bootstrap
- Permutation
- 小结
引言
非参数统计(nonparametric statistics)是相对于参数统计而言的一个统计学分支,是数理统计的重要内容。在参数统计中,我们往往碰到的是这样的情况:
- 总体分布的数学形式已知(例如正态分布、指数分布等)。
- 总体分布的概率密度函数中含有有限个参数。
然而实际情况往往不是这样,我们通常不知道总体分布的数学形式,或者虽然已知总体的分布但却不能用有限个参数去刻画,我们只能对总体做出一些简单的假定(例如总体分布是连续的或者离散的,总体分布是否对称),这时如果我们要对总体的某些性质进行估计或者假设检验,就需要使用非参数方法。
非参数方法是一种不依赖于总体分布具体形式的统计推断方法,构造统计量通常与总体分布无关,也就是说,非参数方法与总体分布无关,因此,非参数方法也被称为自由分布(distribution-free)方法。非参数方法具有如下的特点:
- 适用面广但针对性较差。
- 对变量的量化要求很低。无论是分类变量和数值变量,都可以使用非参数方法进行估计或检验。
- 非参数方法对于数据的要求不如参数方法严格。
- 非参数方法具有较好的鲁棒性,不容易受数据中极端值和离群点的影响。
- 对于符合参数方法条件的数据,使用非参数方法会使犯第二类错误的概率增大,即统计功效会更小。
由以上的特点,我们可以总结出选用参数方法和非参数方法的原则:
- 如果中位数(而不是均值)更能反应数据的集中趋势时(极端值较多),应当选用非参数方法。
- 如果数据为定序变量(如优良中)时,应当采用非参数方法。
- 如果数据符合参数方法的条件时,应当优先选用参数方法。
接下来我们来详细讨论一些非参数方法的例子。
非参数方法举例
Wilcoxon 符号秩检验
Wilcoxon符号秩检验(signed-rank test)对应着参数方法中的单样本t检验法和配对样本t检验法。接下来我们通过一个例子来讲解Wilcoxon符号秩检验的步骤。
假设我们研究的课题是上培训班是否会提升学生成绩,我们收集到的数据如下:
| Before | After |
|---|---|
| 72 | 60 |
| 62 | 86 |
| 70 | 83 |
| 60 | 53 |
| 75 | 75 |
| 55 | 65 |
| 71 | 89 |
| 48 | 56 |
根据这一张表格,我们可以进一步得到这样的另一张表格。
| Diff | Signed-rank |
|---|---|
| -12 | -4 |
| 24 | 7 |
| 13 | 5 |
| -7 | -1 |
| 0 | |
| 10 | 3 |
| 18 | 6 |
| 8 | 2 |
其中,Diff是拿右边一列减去左边一列得到的数据,而得到Signed-rank略显复杂,首先我们将Diff的绝对值从小到大进行排名(rank),分别编上1-n的编号,然后根据Diff的实际符号,给排名也添加上相同的符号,我们就得到了样本的符号秩(signed-rank),我们就由符号秩来构造统计量。
需要注意的是,我们进行Wilcoxon符号秩检验时,不考虑Diff=0的情况,我们要将Diff=0的数据去除。
接下来我们用符号秩来构造统计量 Z Z Z: Z = ∑ i = 1 n S R i ∑ i = 1 n S R i 2 Z = \frac{\sum^n_{i=1}SR_i}{\sqrt{\sum^n_{i=1}SR_i^2}} Z=∑i=1nSRi2∑i=1nSRi
与参数方法中的 Z Z Z统计量一样, Z Z Z~ N ( 0 , 1 ) N(0,1) N(0,1),于是我们算得 Z Z Z统计量之后,就可以通过标准正态分布来计算p值,在上面这个例子中: Z = 1.52 Z=1.52 Z=1.52
我们进行一个双尾检验,查表可得 p − v a l u e = 2 ∗ ( 1 − 0.9357 ) = 0.1286 > 0.05 p-value=2*(1-0.9357)=0.1286>0.05 p−value=2∗(1−0.9357)=0.1286>0.05
得出结论:应当接受零假设,成绩与是否上辅导班无关。
Wilcoxon秩和检验
Wilcoxon秩和检验(rank-sum test)用于检验两个总体的中位数是否相等,适用于中位数能更好的反应总体集中趋势的情况,对应了参数方法中的Two sample t-test,同样我们通过一个例子来讲解Wilcoxon秩和检验的过程。
我们仍然使用上面的表格,只不过我们这次研究的题目是成绩是否与性别有关。(实际上,两列数据的样本容量可以不同)可以发现,这样一来,数据中的行不再是一一对应关系。
| Male | Female |
|---|---|
| 72 | 60 |
| 62 | 86 |
| 70 | 83 |
| 60 | 53 |
| 75 | 75 |
| 55 | 65 |
| 71 | 89 |
| 48 | 56 |
我们将两列数据合在一起,进行从小到大的排序,求出它们的秩(秩的英文为rank,也可以翻译为排名)。
| Rank(Male) | Rank(Female) |
|---|---|
| 11 | 5.5 |
| 7 | 14 |
| 9 | 13 |
| 5.5 | 2 |
| 12.5 | 12.5 |
| 3 | 8 |
| 10 | 15 |
| 1 | 4 |
需要注意的是,当出现多个样本值相同时,它们的秩应当等于它们占用的秩的位置的平均值。接下来我们来构造统计量,首先我们将每一列元素的秩进行求和:
S u m 1 = ∑ i n 1 R 1 Sum1 = \sum_i^{n_1}{R_1} Sum1=i∑n1R1 S u m 2 = ∑ i n 2 R 2 Sum2 = \sum_i^{n_2}{R_2} Sum2=i∑n2R2
设两个变量的样本容量分别是 n 1 n_1 n1, n 2 n_2 n2,我们构造下面的统计量:
W = S u m 1 − n 1 ∗ ( n 1 + 1 ) 2 W=Sum1 - \frac{n_1*(n_1+1)}{2} W=Sum1−2n1∗(n1+1)
同样的,利用 S u m 2 Sum2 Sum2也可以构造一个这样的统计量,但实际上检验一个即可。我们同样避开直接寻找 W W W的分布,我们选择再构造一个统计量:
Z = W − n 1 n 2 / 2 n 1 n 2 ( n 1 + n 2 + 1 ) / 12 Z=\frac{W-n_1n_2/2}{\sqrt{n_1n_2(n_1+n_2+1)/12}} Z=n1n2(n1+n2+1)/12W−n1n2/2
同样的, Z Z Z~ N ( 0 , 1 ) N(0,1) N(0,1),接下来我们就可以在标准正态分布中查找到 P − v a l u e P-value P−value,从而做出是否拒绝零假设的判断。
在上面这个例子中,我们计算得到:
W = 23 W=23 W=23 Z = − 0.945 Z=-0.945 Z=−0.945
查表得到对应的p值为:
p − v a l u e = 2 ∗ ( 1 − 0.8289 ) = 0.3422 > 0.05 p-value=2*(1-0.8289)=0.3422>0.05 p−value=2∗(1−0.8289)=0.3422>0.05所以我们应当接受零假设,成绩与性别无关。
斯皮尔曼相关性检验
在参数统计中,我们学习过一个相关系数 ρ x y \rho_{xy} ρxy,它的定义如下: ρ x y = C o v ( X , Y ) S X S Y \rho_{xy}=\frac{Cov(X,Y)}{S_XS_Y} ρxy=SXSYCov(X,Y)实际上,我们把这个相关系数称为皮尔逊相关系数(Pearson Correlation),而接下来我要介绍的是另一个相关系数,称为斯皮尔曼相关系数(Spearman Correlation)。
首先举一个例子,假设我们研究的课题是学生考试分数与课堂满意度是否相关,我们采集到了这样一组数据:
| Score | Happiness |
|---|---|
| 30 | 不满意 |
| 40 | 一般 |
| 50 | 不满意 |
| 60 | 一般 |
| 70 | 满意 |
| 80 | 满意 |
| 90 | 满意 |
| 100 | 满意 |
可以看到,这里的Happiness数据是定序变量,我们没有办法计算它的方差和它与定距变量的协方差,但我们可以对它们进行排序,参考前两种方法,我们这两列数据分别排序并求出它们的秩。
| Rank(Score) | Rank(Happiness) |
|---|---|
| 1 | 1.5 |
| 2 | 3.5 |
| 3 | 1.5 |
| 4 | 3.5 |
| 5 | 6.5 |
| 6 | 6.5 |
| 7 | 6.5 |
| 8 | 6.5 |
同样的,对于相同的样本值,我们也要采用取平均值的方法求它们的秩。接下来我们对这两列秩求它们的皮尔逊相关系数,得到的就是原数据的斯皮尔曼相关系数:
ρ = C o v ( R 1 , R 2 ) S R 1 S R 2 \rho=\frac{Cov(R_1,R_2)}{S_{R_1}S_{R_2}} ρ=SR1SR2Cov(R1,R2)另外还有一个简便计算公式,设样本容量为 n n n:
ρ = 1 − 6 ∑ d i 2 n ( n 2 − 1 ) \rho=1-\frac{6\sum{d_i^2}}{n(n^2-1)} ρ=1−n(n2−1)6∑di2然后,与参数方法中的皮尔逊相关性检验类似,有:
ρ 1 − ρ 2 / n − 2 ∼ t ( n − 2 ) \frac{\rho}{\sqrt{1-\rho^2}/\sqrt{n-2}}\sim t(n-2) 1−ρ2/n−2ρ∼t(n−2)
然后在 t t t分布中计算 p − v a l u e p-value p−value,做出判断。
Bootstrap
Bootstrap简单的来说,我们已有一个容量为 n n n的原始样本,利用随机数等方式进行放回抽样得到一个容量同样为 n n n的样本,这种样本就称为Bootstrap样本或自助样本。
我们反复地、独立地从原始样本中抽取很多很多个Bootstrap样本(通常不少于1000个),利用这些样本对总体进行统计推断,这种方法被称为非参数Bootstrap方法,又称为自助法。
我们使用成绩与性别关系的数据:
| Male | Female |
|---|---|
| 72 | 60 |
| 62 | 86 |
| 70 | 83 |
| 60 | 53 |
| 75 | 75 |
| 55 | 65 |
| 71 | 89 |
| 48 | 56 |
我们对两列数据进行有放回抽样,得到了1000个Bootstrap样本,记作 D 1 D_1 D1- D 1000 D_{1000} D1000。我们需要分析的是两个样本之间的中位数是否有差异,因此我们将每一个Bootstrap样本的中位数差值求出来,用这1000个数据的中位数差构成一个统计分布,用直方图表示:
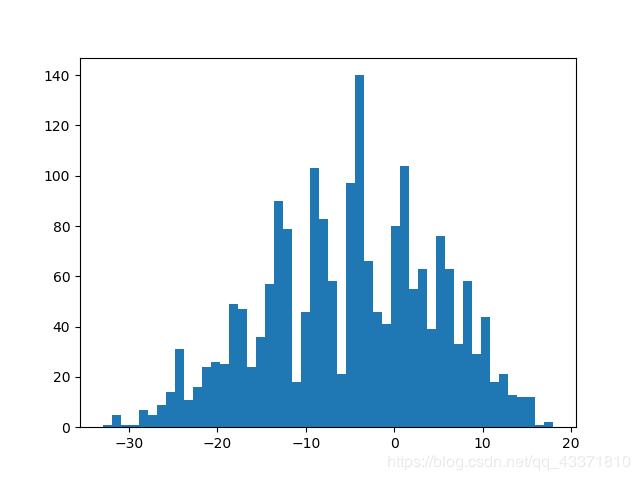
然后我们再根据已知的中位数差值,在这个统计分布中计算p值、置信区间等,做出统计推断。
Bootstrap是一种非常重要的方法,常常应用于各种玄学建模 。需要注意的是Bootstrap方法也有参数版本的方法,在这里并不讨论。
Bootstrap实现的Python代码如下:
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
def bootstrap(data):
temp = []
while len(temp) != len(data):
r = np.random.randint(0,len(data))
temp.append(data[r])
temp = np.array(temp)
return temp
if __name__ == "__main__":
male = np.array([72,62,70,60,75,55,71,48])
female = np.array([60,86,83,53,75,65,89,56])
v = []
for i in range(2000):
mbootstrap = bootstrap(male)
fbootstrap = bootstrap(female)
v.append(np.median(mbootstrap) - np.median(fbootstrap))
v = np.array(v)
plt.hist(v,bins=50)
plt.show()
Permutation
Permutation,翻译为中文就是排列、置换的意思。在参数方法中进行假设检验,我们一般是假设或者已知总体的分布,然后构造统计量,得到这个统计量在零假设为真时的抽样分布,然后在抽样分布中计算p值,做出推断。而Permutation使得我们可以得到对任意统计量在零假设为真时的抽样分布,从而进行统计推断。接下来我们举例说明Permutation的过程。
我们仍然使用成绩与性别的关系数据:
| Male | Female |
|---|---|
| 72 | 60 |
| 62 | 86 |
| 70 | 83 |
| 60 | 53 |
| 75 | 75 |
| 55 | 65 |
| 71 | 89 |
| 48 | 56 |
H 0 : 男 女 成 绩 中 位 数 没 有 差 异 H_0:男女成绩中位数没有差异 H0:男女成绩中位数没有差异 H 1 : 男 女 成 绩 中 位 数 有 差 异 H_1:男女成绩中位数有差异 H1:男女成绩中位数有差异
Permutation与Bootstrap类似,我们也需要将以下的步骤重复1000次以上:
- 把所有数字随机分配给Male( n 1 = 8 n_1=8 n1=8)和Female( n 2 = 8 n_2=8 n2=8)
- 计算Male和Female的中位数
- 计算并保存median(M)-median(F)
重复1000次以上之后,我们就可以得到两组数据中位数差的近似分布,用直方图表示:
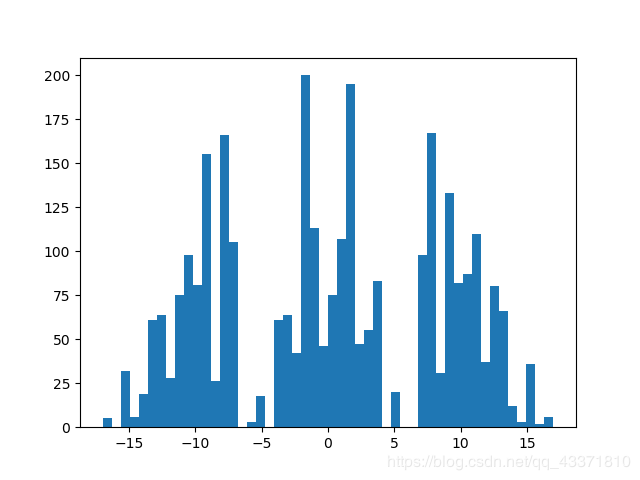
这样我们就获得了中位数差统计量的统计分布,然后我们根据这个分布和实际的中位数差,我们就可以计算出p值,从而进行统计推断。
Permutation的Python代码如下:
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
def permutation(data):
perm = []
num = set([])
while len(perm) != len(data):
r = np.random.randint(0, 16)
if r not in num:
perm.append(data[r])
num.add(r)
perm = np.array(perm)
return perm
if __name__ == "__main__":
data = np.array([72, 62, 70, 60, 75, 55, 71, 48, 60, 86, 83, 53, 75, 65, 89, 56])
diff = []
for i in range(3000):
temp = permutation(data)
df = np.median(temp[:8]) - np.median(temp[8:])
diff.append(df)
diff = np.array(diff)
plt.hist(diff, bins=50)
plt.show()
小结
在这一篇博文中,我主要介绍以下几种非参数统计方法:
- Wilcoxon符号秩检验
- Wilcoxon秩和检验
- Spearman相关性检验
- Bootstrap
- Permutation
但无论是参数方法还是非参数方法都属于频率论的范畴,它们都存在着一个致命的缺陷:它们的检验过程是在假定零假设成立的情况下进行的,为了解决这个问题,需要把目光投向另一个统计学领域——贝叶斯统计。