Red-Black Tree 红黑树
如果viewer对Red-Black Tree先前没有任何了解,可以看看先搞定AVL树,因为AVL树比红黑树要简单的多
涉及同样的rotate技巧,搞懂了AVL树再和红黑大战三百回合绝对轻松的多。
(我见过讲AVL最好的教程就是 Mark Allen Weiss 写的《数据结构与算法分析 C语言描述》里面讲AVL树的部分)
AVL树的C语言实现:
http://blog.csdn.net/cinmyheart/article/details/20527037
Here we go ~ 笔记贴~
----------------------------------------------------------------------------------------------------------------------------------------
Red-BlackTree
这颗神树肿么来的,为嘛就这么神捏?如下:碉堡的性能
如下即为一个红黑树的例子:
红黑树之所以有之前提到的那么好的性能(搜索,删除,插入各种 lg N),是因为它本身设计时具有很好的性质:
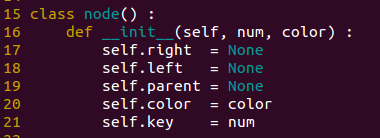
树中的每个节点至少包含五个域:
color, key,left,right,和p(parent)
据此,我们可以对节点进行抽象(Python实现):
1. Every node is either red or black.
2. The root is black.
3. Every leaf ( NIL ) is black.
4. If a node is red, then both its children are black.
5. For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
前三点都很容易掌握,一开始接触Red Black Tree需要特别注意第4和第5条性质。
We call the number of black nodes on any simple path from, but not including, a node x down to a leaf the black-height of the node, denotedbh(x).By property 5, the notion of black-height is well defined, since all descending simple paths from the node have the same number of black nodes. We define the black-height of a red-black tree to be the black-height of its root.
一颗有n个内节点的红黑树的高度至多为2lg(n+1)。关于这个性质的证明CLRS上有详细的证明,非常值得一看。
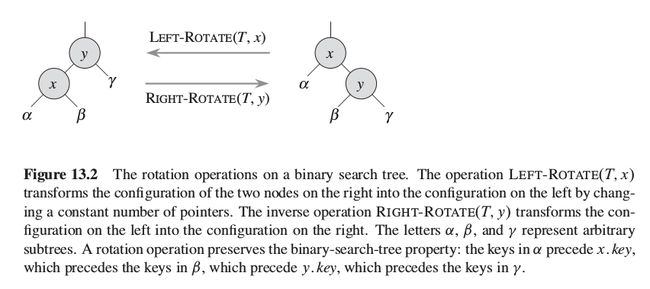
左旋,右旋操作:
做个“神奇”的操作不要想多了,首先别怕。。。
本质上就是节点的交换位置,而且很有规律。
对于右旋,就是像下图中x,y节点的布局一样,当节点x位于y的左下放时,可以通过提升x的高度,降低y的高度,调整,α β γ 三个子树和x,y节点的关系,进而保持二叉树的特性,最后实现x节点的提升。
而左旋就是右旋的逆过程而已。
这里之所以称为左旋右旋,这里的旋是因为“看起来”好像按照上面位置节点(对于左旋,上面位置节点就是y)
的竖直中轴旋转180°,好像就可以从左边的状态变成右边的状态,但是还要调整一下节点关系。这就是“旋”称呼的来源,rotation。
具体用代码实现时,只要死磕节点关系,按照下面的状态转换图进行调整即可。
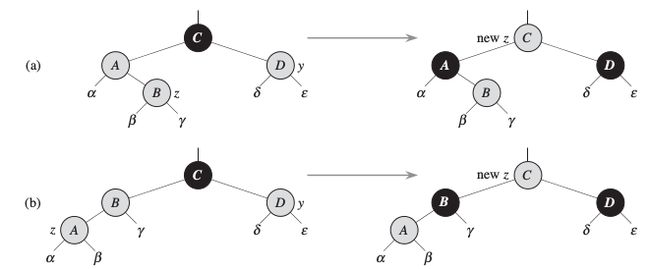
对于节点的插入:
三种情况:
Case 1: ́’s uncle y is red
策略很简单就是把z.parent的黑节点“沉降”下来。
Case 2: ́’s uncle y is black and ́ is a right child
Case 3: ́’s uncle y is black and ́ is a left child
策略也比较简单,就是先在case 2里对A节点左旋,然后进入了case 3 对C节点右旋,并调整节点颜色。
"""
Code writer : EOF
Code date : 2015.01.29
Code file : rbt.py
e-mail : [email protected]
Code description :
Here is a implementation of red-black-tree in Python.
If you find something wrong with my code, please touch me
by e-mail. Thank you!
"""
class node() :
def __init__(self, num, color) :
self.right = None
self.left = None
self.parent = None
self.color = color
self.key = num
class Red_Black_Tree() :
def __init__(self, array) :
self.nil = node(0, 'black')
self.root = self.nil
for i in range(0,len(array)) :
self.rb_insert(array[i])
def rb_search(node, num) :
if node.key > num :
return rb_search(node.left, num);
elif node.key < num :
return rb_search(node.right, num);
else :
return node
def tree_mininum(self, x) :
while x.left != self.nil :
x = x.left
return x
def tree_successor(self, x) :
if x.right != self.nil :
return self.tree_mininum(x.right)
y = x.parent
while y != self.nil and x == y.right :
x = y
y = y.parent
return y
def left_rotate(self, x) :
y = x.right
x.right = y.left
if y.left is not self.nil :
y.left.parent = x
if x.parent is self.nil :
self.root = y
elif x is x.parent.left :
x.parent.left = y
else :
x.parent.right = y
y.parent = x.parent
y.left = x
x.parent = y
def right_rotate(self, x) :
y = x.left
if y.right is not self.nil :
y.right.parent = x
if x.parent is self.nil :
self.root = y
elif x is x.parent.left :
x.parent.left = y
else :
x.parent.right = y
y.parent = x.parent
y.right = x
x.parent = y
def rb_insert(self, num) :
z = node(num, 'red')
z.right = self.nil
z.left = self.nil
z.parent = self.nil
y = self.nil
x = self.root
while x != self.nil :
y = x
if z.key < x.key :
x = x.left
else :
x = x.right
z.parent = y
if y is self.nil :
self.root = z
elif z.key < y.key :
y.left = z
else :
y.right = z
z.left = self.nil
z.right = self.nil
z.color = 'red'
self.rb_insert_fixup(z)
def rb_insert_fixup(self, z) :
while z.parent.color is 'red' :
if z.parent is z.parent.parent.left :
y = z.parent.parent.right # @y is the uncle of @z
if y.color is 'red' : # $case 1
z.parent.color = 'black'
y.color = 'black'
z.parent.parent.color = 'red'
z = z.parent.parent
else : # here is the color of uncle-node @y is 'black'
if z is z.parent.right : # $case 2
z = z.parent
self.left_rotate(z)
z.parent.color = 'black' # $case 3
z.parent.parent.color = 'red'
self.right_rotate(z.parent.parent)
else : # In this situation, p[z] == right[p[p[z]]]
y = z.parent.parent.left
if y.color is 'red' :
z.parent.color = 'black'
y.color = 'black'
z.parent.parent.color = 'red'
z = z.parent.parent
else :
if z is z.parent.left :
z = z.parent
self.right_rotate(z)
z.parent.color = 'black'
z.parent.parent.color = 'red'
self.left_rotate(z.parent.parent)
self.root.color = 'black'
def __str__(self):
def recurse(node) :
if node is None:
return [], 0, 0
else :
left_lines, left_pos, left_width = recurse(node.left)
right_lines, right_pos, right_width = recurse(node.right)
label = str(node.key) + ' ' + str(node.color)
middle = max(right_pos + left_width - left_pos +1, len(label), 2)
pos = left_pos + middle//2
width = left_pos + middle + right_width - right_pos
while len(left_lines) < len(right_lines) :
left_lines.append(' ' * left_width)
while len(right_lines) < len(left_lines) :
right_lines.append(' ' * right_width)
line = [ ' ' * left_pos + label +
' ' * (right_width-right_pos + 1),
' ' * left_pos + '/' +
' ' * (middle-2) + '\\' +
' ' * (right_width - right_pos)
] + \
[
left_line +
' ' * (width - left_width - right_width) +
right_line
for left_line, right_line
in zip(left_lines, right_lines)
]
if node is self.root :
return line
else :
return line, pos, width
if self.root is None :
return ''
output = recurse(self.root)
for i in range(1, len(output)-2) :
output[0] += '\n' + output[i]
return output[0]+'\n'
#----------- for testing ------------------------------
array = [1,2,4,5,7,8,11,14,15]
my_little_tree = Red_Black_Tree(array)
print my_little_tree 测试结果:
树形结构还待改进~ 不过不影响测试。能看清楚,凑合
-----------------------------------------------------------------------------------------------------------
删除节点嘛~ 要重点扯一扯所以先上代码,然后后续再分析。。。
女神啊~