数据分析相关知识点整理-统计
参考微信公众号 数据不吹牛
https://mp.weixin.qq.com/s/QQaCdF5hXjSlDJQ4obw3kw
1. 扑克牌54张,平均分成2份,求这2份都有2张A的概率。
- C(4,2)*C(50,25)/C(54,27)
2. 男生点击率增加,女生点击率增加,总体为何减少?
- 因为男女点击率可能存在较大差异,基数不同,最终占比结果也不一样。同时低点击率群体的占比增大
- 如原来男性20人,点击1人;女性100人,点击99人,总点击率100/120。
- 现在男性100人,点击6人;女性20人,点击20人,总点击率26/120。
- 即那个段子“A系中智商最低的人去读B,同时提高了A系和B系的平均智商。”
3. 参数估计和假设检验
- 参数估计和假设检验是统计推断的两个组成部分,它们都是利用样本对总体进行某种推断,但推断的角度不同。
- 参数估计用样本统计量去估计总体的参数,总体参数miu在估计之前是未知的
- 假设检验先对miu的值提出一个假设,然后再用样本信息去检验这个假设是否成立
4. 置信度、置信区间
- 置信区间使我们所计算出的变量存在的范围,置信度是我们对于这个数值存在于我们计算出的这个范围的可信程度
- 举例来讲,有95%的把握,真正的数值在我们所计算的范围里。
- 在这里,95%是置信水平,而计算出的范围,就是置信区间。
- 如果置信度为95%, 则抽取100个样本来估计总体的均值,由100个样本所构造的100个区间中,约有95个区间包含总体均值。
5. 协方差与相关系数的区别和联系
参考https://blog.csdn.net/YPP0229/article/details/100519343
-
协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。

-
相关系数是研究变量之间线性相关程度的量,取值范围是[-1,1]。是协方差的标准化、归一化形式,消除了量纲、幅值变化不一的影响。实际应用中,在比较不同变量之间相关性时,使用相关系数更为科学和准确。但是协方差在机器学习的很多领域都有应用,而且非常重要!

-
为什么除以各自变量的标准差就能消除幅值影响呢?
这是因为标准差本身反映了变量的幅值变化程度,除以标准差正好能起到抵消的作用,让协方差标准化。这样,相关系数的范围就被归一化到 [-1,1] 之间了。 -
相关系数大于零,则表示两个变量正相关,且相关系数越大,正相关性越高;
-
相关系数小于零,则表示两个变量负相关,且相关系数越小,负相关性越高;
-
相关系数等于零,则表示两个变量不相关。
6. 中心极限定理
- 中心极限定理定义:
(1)任何一个样本的平均值将会约等于其所在总体的平均值。
(2)不管总体是什么分布,任意一个总体的样本平均值都会围绕在总体的平均值周围,并且呈正态分布。 - 中心极限定理作用:
(1)在没有办法得到总体全部数据的情况下,我们可以用样本来估计总体。
(2)根据总体的平均值和标准差,判断某个样本是否属于总体。
7. p值的含义。
基本原理:
a、一个命题只能证伪,不能证明为真
b、在一次观测中,小概率事件不可能发生
c、在一次观测中,如果小概率事件发生了,那就是假设命题为假
p值可通过计算chi-square后查询卡方分布表得出,用于判断H0假设是否成立的依据。
p值计算卡方检验参考
卡方检验是一种用途很广的计数资料的假设检验方法。它属于非参数检验的范畴,主要是比较两个及两个以上样本率( 构成比)以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。
通过分析期望值和观测值的差距,我们就可以判断出硬币是否正常。而这个期望值和观测值差距的判断方法就是chi-square。
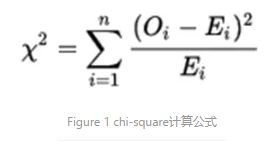
上图即为chi-square的计算公式,O代表观测值(observed value),E代表期望值(expected value)。有没有觉得这和方差的公式很像?没错,其实方差是一组数据与其均值的比较,而chi-suaqre是一组数据与另一组数据期望值的比较。
那么在掷硬币这个例子中chi-square(卡方)=![]()

p-value的计算:计算chi-suqare,计算自由度,查卡方分布表。
总的思路是:
做出H0,H1这对互斥的假设,计算出H0为真时的期望值,统计出实际的观测值,通过期望值和观测值求得chi-square(卡方),再通过卡方查表,得到p值。根据p值与α(1-置信度)的比较,如果p-value<α,则拒绝(reject)H0,推出H1成立;如果p-value>α,则接受(accpet)H0,推出H1不成立。
可以看到p越小→这个事件越是小概率事件→否命题越可能被推翻→原命题越可信。
8.时间序列分析
是同一现象在不同时间上的相继观察值排列而成的序列。

9.怎么向小孩子解释正态分布
拿出小朋友班级的成绩表,每隔2分统计一下人数(因为小学一年级大家成绩很接近),画出钟形。然后说这就是正态分布,大多数的人都集中在中间,只有少数特别好和不够好
拿出隔壁班的成绩表,让小朋友自己画画看,发现也是这样的现象,然后拿出班级的身高表,发现也是这个样子的
大部分人之间是没有太大差别的,只有少数人特别好和不够好,这是生活里普遍看到的现象,这就是正态分布
10. 下面对于“预测变量间可能存在较严重的多重共线性”的论述中错误的是?
A. 回归系数的符号与专家经验知识不符(对)
B. 方差膨胀因子(VIF)<5(错,大于10认为有严重多重共线性)
C. 其中两个预测变量的相关系数>=0.85(对)
D. 变量重要性与专家经验严重违背(对)
11. PCA为什么要中心化?PCA的主成分是什么?
因为要算协方差。
单纯的线性变换只是产生了倍数缩放,无法消除量纲对协方差的影响,而协方差是为了让投影后方差最大。
在统计学中,主成分分析(PCA)是一种简化数据集的技术。它是一个线性变换。这个变换把数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。
主成分分析经常用减少数据集的维数,同时保持数据集的对方差贡献最大的特征。这是通过保留低阶主成分,忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。但是,这也不是一定的,要视具体应用而定。
主成分分析的原理是设法将原来变量重新组合成一组新的相互无关的几个综合变量,同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析,也是数学上处理降维的一种方法。主成分分析是设法将原来众多具有一定相关性(比如P个指标),重新组合成一组新的互相无关的综合指标来代替原来的指标。
通常数学上的处理就是将原来P个指标作线性组合,作为新的综合指标。最经典的做法就是用F1(选取的第一个线性组合,即第一个综合指标)的方差来表达,即Va(rF1)越大,表示F1包含的信息越多。因此在所有的线性组合中选取的F1应该是方差最大的,故称F1为第一主成分。
如果第一主成分不足以代表原来P个指标的信息,再考虑选取F2即选第二个线性组合,为了有效地反映原来信息,F1已有的信息就不需要再出现再F2中,用数学语言表达就是要求Cov(F1,F2)=0,则称F2为第二主成分,依此类推可以构造出第三、第四,……,第P个主成分。
12. 极大似然估计
利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。