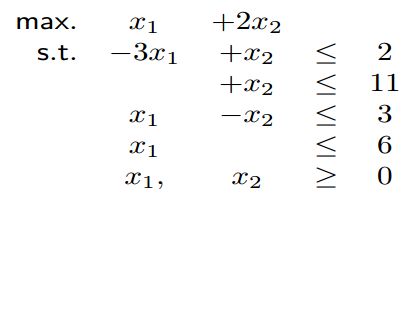2019独角兽企业重金招聘Python工程师标准>>> ![]()
最近在做一个叫交通最小通勤计算问题,需要用到线性规划来解决,因此在网上搜了一下啊线性规划工具,因为不想装MATLAB,(实在是太大了,电脑c盘剩下不到4g了)就找了一个开源的线性规划小工具,感觉还蛮实用的,GNU Linear Programming Kit (GLPK http://gnu.april.org/software/glpk/ )一个开源的线性规划工具,再这里给大家介绍介绍。
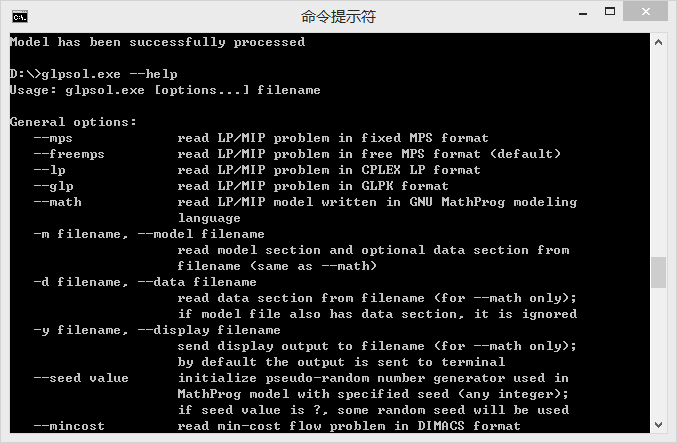
glpsol.exe就是主程序了,glpsol.exe主要是通过命令行运行,可以通过 --help 命令了解下他的主要命令:
GLPK所使用的编译语言主要是 GNU MathProg language,我主要尝试了glpsol的两个命令--math 和 --model,分别介绍下:
线性规划方程:
本案列就用Sriram在Coursera公开课的上讲的案例直接进行介绍了,math方法是最简单的方法,就是直接把线性方程写下来,找一个txt记事本:
var x1>=0;
var x2>=0;
maximize obj:x1+2*x2;
c1:-3*x1+x2<=2;
c2:x2<=11;
c3:x1-x2<=3;
c4:x1<=6;
solve;
display x1;
display x2;
end;可以看出MathProg language很简单,定义变量范围var,定义目标maximize obj:和约束条件就可以了,最后求解solve和显示display 然后保持为first.ampl
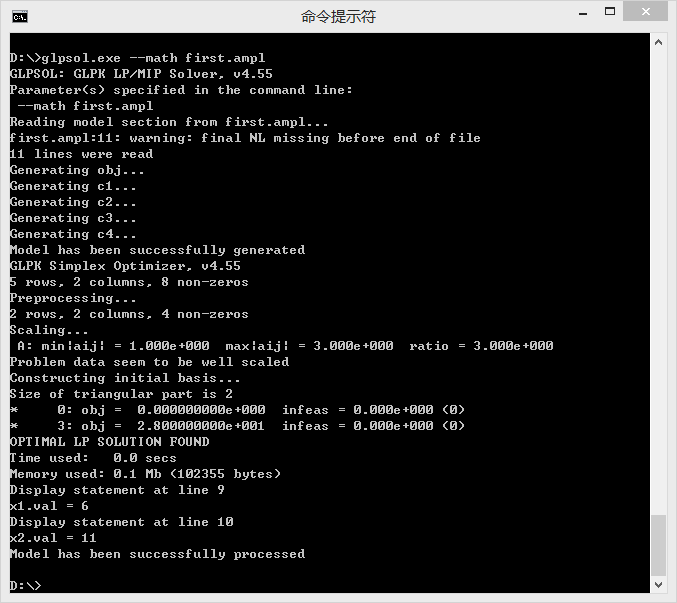
在CMD命令行直接输入glpsol --math fitst.ampl就可以了
可以看到结果为x1=6,x2=11;内存使用0.1Mb
这种方法在解决简单少量的线性规划的时候很简单清晰,但是在解决大量线性规划的时候是不具备可操作性的,因此介绍GLPK的第二种命令--model,这种命令可以用两个文件存储一个为MODEL文件,一个为DATA文件,MODEL文件主要通过构建矩阵进行线性规划计算,同样以上面的线性规划为例,可以得出其实上面的约束方程可以看出两个矩阵相乘,分别为一个系数矩阵A和所求矩阵X相乘小于等于b矩阵(A*x<=b):
param m;
param n;
param c{i in 1..n};
param A{i in 1..m,j in 1..n};
param b{i in 1..m};
var x{i in 1..n}>=0;
maximize obj:sum{i in 1..n} c[i]*x[i];
s.t.
e{j in 1..m}:sum{i in 1..n} A[j,i]*x[i]<=b[j];
solve;
display x;
end;写完model文件还需要写一个赋值的data文件对model中的参数赋值:
param n:=2;
param m:=4;
param c:=1 2:
1 2;
param A:=1 2:
1 -3 1
2 0 1
3 1 -1
4 1 0;
param b:= 1:
1 2
2 11
3 3
4 6;具体data文件的写作格式可以参考( http://pan.baidu.com/s/1i3CDq8t )
里面有详细说明,
然后只要再在cmd中用命令--model执行就可以了:
结果和math命令一样,不过内存使用稍微大了点。还有很多新的功能,但是没探索了,先解决完自己的小问题先吧~~呜呜,今天光棍节,凄惨。。
http://my.oschina.net/Kanonpy/