pymprog库应用(一)工位规划--生产线平衡
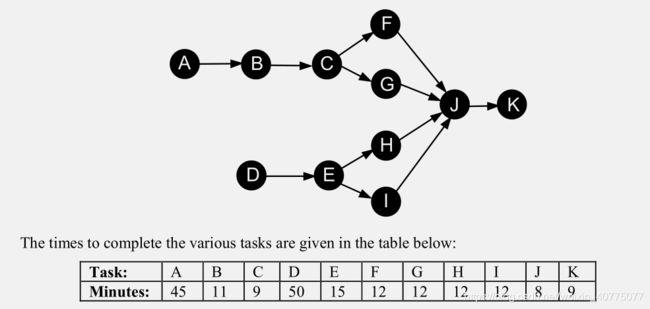
问题描述
问题分析
设置不同的工位数,进行求解,评价工位平衡状态。
求解
设置工位数为5
求解得到:
工位1:[‘A’]
工位2:[‘B’]
工位3:[‘D’]
工位4:[‘C’, ‘E’, ‘F’, ‘I’]
工位5:[‘G’, ‘H’, ‘J’, ‘K’]
节拍时间:50.0
工位时间:
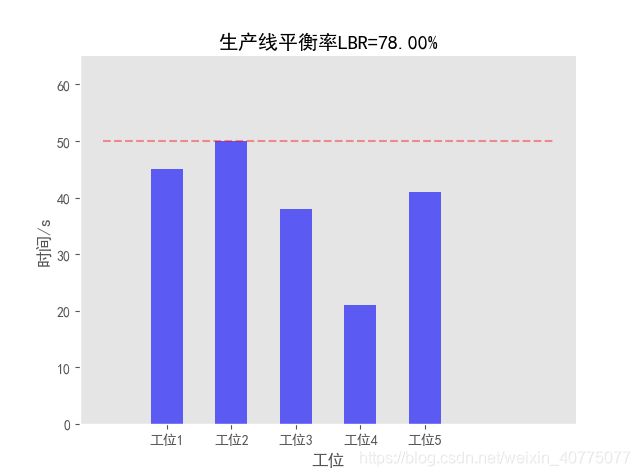
[45, 11, 50, 48, 41]
平衡率LBR: 78.00%
平衡损失率d: 22.00%
平滑性指数SI: 18.06
平衡状态: 差
设置工位数为3
求解得到:
工位1:[‘D’, ‘E’]
工位2:[‘A’, ‘B’, ‘C’]
工位3:[‘F’, ‘G’, ‘H’, ‘I’, ‘J’, ‘K’]
节拍时间:50.0
工位时间:
[65, 65, 65]
平衡率LBR: 100.00%
平衡损失率d: 0.00%
平滑性指数SI: 0.00
平衡状态: 优

平衡率最高时,工位划分如下。此时节拍为65,比50大很多。再考虑,工位数为4的情况。

设置工位数为4
求解得到:
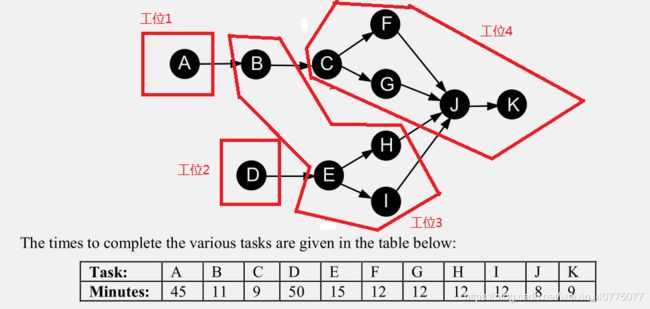
工位1:[‘A’]
工位2:[‘D’]
工位3:[‘B’, ‘E’, ‘H’, ‘I’]
工位4:[‘C’, ‘F’, ‘G’, ‘J’, ‘K’]
节拍: 50.0
工位时间:
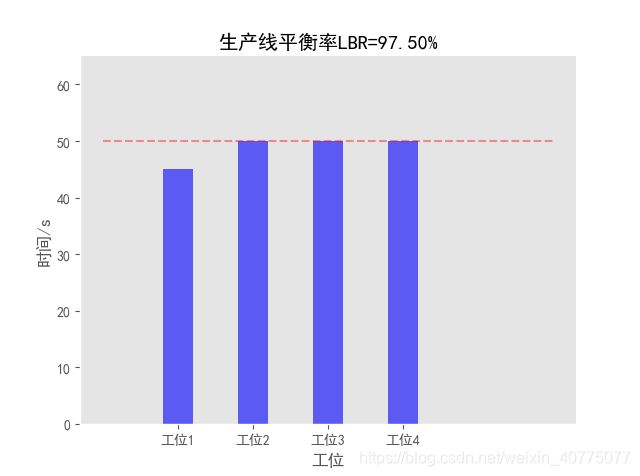
[45, 50, 50, 50]
平衡率LBR: 97.50%
平衡损失率d: 2.50%
平滑性指数SI: 2.50
平衡状态: 优
代码(生产线平衡)
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.style.use('ggplot')
def _balance(t):
#
# 计算平衡状态
#
n = len(t)
ct = max(t)
lbr = sum(t) / (n * ct)
d = 1 - lbr
a = 0
for i in t:
a += pow((ct - i), 2)
si = pow(a / n, 0.5)
if d <= 0.1:
cm = '优'
elif d <= 0.2:
cm = '良'
else:
cm = '差'
return lbr * 100, d * 100, si, cm
def _bar(data, ct, xlabel, ylabel, xticks, setdpi, lbr):
#
# 绘制平衡图
#
index = np.arange(1, len(data) + 1)
plt.grid(False) # 不显示网格
bar_width = len(data) / 10 # 条形图宽度
plt.bar(index, data, width=bar_width, color='blue', alpha=0.6) # 绘制条形图
plt.ylim(0, 1.30 * max(data)) # 设置y轴范围
ct = ct
plt.plot([ct] * int(1.75 * len(data)), 'r--', alpha=0.4)
# 图形属性设置及文字标注
plt.xlabel(xlabel) # 设置x轴的标签
plt.ylabel(ylabel) # 设置y轴的标签
plt.xticks(range(1, len(xticks) + 1), xticks) # 设置x轴的显示名称
plt.title( "生产线平衡率LBR=")
# 设置边框是否显示
ax = plt.gca()
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
plt.savefig("result.jpg", dpi=setdpi)
plt.show()
def status(data, ct):
#
# 平衡状态
#
t = data
ct = ct
lbr, d, si, cm = _balance(t)
xlabel = "工位"
ylabel = "时间/s"
xticks = []
for i in range(1, len(t) + 1):
xticks.append("工位%d" % i)
setdpi = 720
_bar(t, ct, xlabel, ylabel, xticks, setdpi, lbr)
def result(t):
#
# 输出结果
#
lbr, d, si, cm = _balance(t)
print(str.format("平衡率LBR: {0:0.2f}%\n平衡损失率d: {1:0.2f}%\n平滑性指数SI: {2:0.2f}\n平衡状态: {3}", lbr, d, si, cm))
代码(pymprog数学模型)
from pymprog import *
import numpy as np
from ie.balance import result, status
def main():
begin('assembly balance')
job = np.load('a_datajob.npy').tolist()
jobtime = np.load('a_datatime.npy').tolist()
jobseqe = np.load('a_dataseq.npy').tolist()
station = np.load('a_datastation.npy').tolist()
ipo = iprod(job, station)
x = var('x', ipo, kind=bool)
ct = var('ct', kind=int)
minimize(ct, 'cycle time')
for i in job: # 每个工序必须安排一个工位
sum(x[i, k] for k in station) == 1
for s in jobseqe: # 工序顺序约束
sum(k * x[s[1][-1], k] - k * x[s[0][0], k] for k in station) >= 0
for k in station: # 工位时间约束
sum(x[i, k] * jobtime[i] for i in job) <= ct
def report():
res = [] # 工序-工位
for i in job:
for j in station:
if x[i, j].primal > 0:
res.append([i, j])
res.sort(key=lambda x: x[1])
np.save('a_databalance.npy', res)
st = [] # 工位-工序
for i in station:
temp = []
for j in range(len(res)):
if res[j][1] == i:
temp.extend(res[j][0])
st.append(temp)
tm = [] # 工位-时间
for s in st:
temp = 0
for j in s:
temp += jobtime[j]
tm.append(temp)
for i in range(len(st)):
print("工位{}:{}".format(i + 1, st[i]))
print("节拍:",ct.primal)
print("工位时间:\n", tm)
result(tm)
status(tm, ct.primal)
solve()
report()
end()
if __name__ == "__main__":
main()
代码(模型数据)
import numpy as np
job = "A,B,C,D,E,F,G,H,I,J,K".split(",")
jobtime = [45, 11, 9, 50, 15, 12, 12, 12, 12, 8, 9]
jobseq = [('A, B'), ('B, C'), ('C, F'), ('C, G'), ('F, J'),
('G, J'), ('D, E'), ('E, H'), ('E, I'), ('H, J'),
('I, J'), ('J, K')
]
station = range(1, 5) # 设置工位数为3
def main():
datajob = job
datatime = {}
dataseq = jobseq
for i in range(len(job)):
datatime[job[i]] = jobtime[i]
for i in range(len(jobseq)):
jobseq[i] = jobseq[i].split(',')
np.save('a_datajob.npy', datajob)
np.save('a_datatime.npy', datatime)
np.save('a_dataseq.npy', dataseq)
np.save('a_datastation.npy', station)
a = np.load('a_datajob.npy')
b = np.load('a_datatime.npy')
c = np.load('a_dataseq.npy').tolist()
d = np.load('a_datastation.npy')
print("工序名称")
print(a)
print("工序时间")
print(b)
print("工序顺序")
print(c)
print("工位数")
print(d)
if __name__ == "__main__":
main()