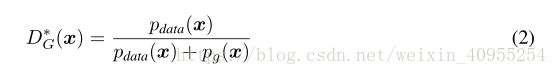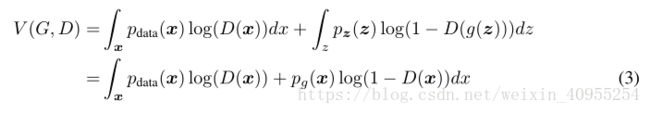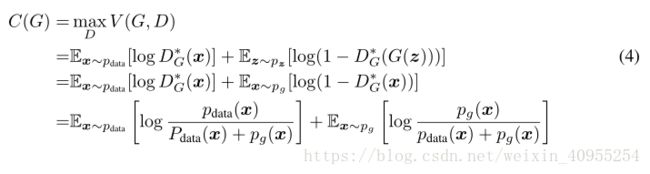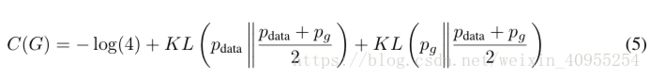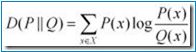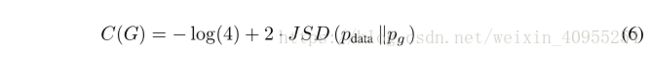Generative Adversarial nets（GAN）学习笔记

很早之前就对于对抗网络（GAN）这样一个大名鼎鼎的网络心生向往，也看过一些别人的博文，由于没有特殊的应用背景或者使用目的，所以一直以来了解也不是特别的深刻。上周在看ReID系列的论文，在“A camera style adaption for person Reld”里面，他提到使用的网络就是GAN，于是找出J.Goodfellow这篇2014年的论文，好好的拜读了一下。

序

先给大家讲一个故事，有一伙犯罪分子想要去制造假钞混进市场使用，从而不法牟利。而银行系统则需要依靠相关技术鉴别出假钞来。不法分子为了让自己利益最大化，需要不断地提高自身的造价能力；而银行系统为了能够准确的识别出假钞也需要不断地提高自己的识别能力。双方的技术在这个竞争的过程中得到不断地提高，最后达到一个最佳的水平是什么呢，就是银行系统的是必然率为50%，双方都达到最高的要求，没有办法再进一步了。

摘要

我们提出了一个框架通过对抗过程估计生成模型，在这个框架中包含了两个部分：一个生成模型G用来捕获数据分布，一个判别模型D用来判断一个浪奔来自初始数据以及G生成模型的可能性。对于G的训练过程就是去最大化让D判别失误的可能性。这个过程就像上述序中的例子，在两个模型G和D中存在一个独特的解，就是G能够完整的恢复出原始数据而判别器D判别成功的概率是1/2.

正文

在这个文章中，我们研究室是这样一个特殊情况，通过向模型里输入一段噪声能够利用生成模型G生成一个样本。生成模型G和判别模型都是多层感知结构。我们将上述这种情况称为对抗网络。在这个框架中，两个模型都可以使用后向传播和dropout进行训练。

在两个模型都是多层感知界都的基础上往往直接使用对抗网络。为了学习生成器对于输入数据x的分布pg，我们首先定义了一个噪声变量pz（z），然后模型G（z，θ g ）表示了从噪声到数据空间的映射，θ g是参数，此外我们还定义了D（x，θ d）输出一个简单的数，表示数据来自原始数据空间还是由噪声通过G生成的。我们训练D区最大化能够正确识别出真假样本的。我们训练G就是为了最小化这个方程：

换句话说，D和G进行如下的两个玩家的最大最小对抗游戏，方程如下：

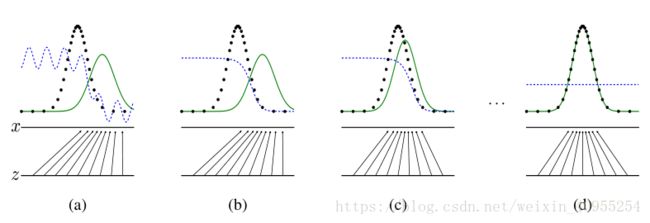
最小化这个方程的右边部分就是在训练G，最大化这个方程的左边部分就是在训练D，下面给大家看一下图一：

由a到d代表了整个网络的训练过程，其中黑色的线代表了初始样本的分布，绿色的代表生成模型对于初始样本分布的估计，蓝色的线代表判别器对于样本估计的准确率。下面由z轴指向x轴的线表示生成器G生成样本的分布趋势。所以d中那条蓝色的线水平值不闲，对应的应该是0.5，表示的是生成器和判别器达到均衡，双方不再发生变化。

在测试中，这两个模型是串联的，但是在训练中他们没有办法同时训练，所以我们在训练中采用了一种迭代轮训的方法，首先用内循环去优化D，当然一开始G肯定不是最优的。并且在有限的数据上进行是禁止且会导致过拟合，所以我们采用优化K次D，优化一次G。在G的优化过程中，D的结果靠近它的最优结果。具体可见下方算法一

生成器G定义了一个分布概率pg作为样本分布的概率从输入z ∼ p z 获得，因此我们希望pg可以收敛到符合x的分布。接下来我们将展示当pg=pdata=0.5的时候整个模型达到了最优。

我们首先考虑对于任意给定的G，如何去优化D，其实可以表示为下面这个方程

依据上面的方程一，给定G，我们的目的就是去最大化方程一，那么方程一可以写成下面的形式：

存在这样一个理论，对于a，b属于实数范围，方程 y → alog(y) + blog(1 − y)在y取a/（a+b）的时候取得最大值。哦按别气的范围应该是在pg和pdata的交集里面。

注意到对于判别器D的训练可以被视为最大化P(Y = y|x)，Y代表x样本来自哪里，y=0来自G，y=1来自原始数据，所以方程1又可以写成：

定理一：有且只有当Pg=Pdata的时候，C(G)所能达到的全局最小。在那个时候，C（G）达到最小值-log4

证明：如果Pg=Pdata， D ∗G (x)=0.5，因此通过引入方程四，我们得到C（G）=-log4.

通过 从方程四中加上这个，我们获得了：

KL是Kullback-Leibler散度，我们在之前的表达式中获得了Kullback-Leibler散度在模型中，或许大家这里会有疑问，怎么就变成了方程五呢，大家看一下下面的Kullback-Leibler散度公式

这后面两个Kullback-Leibler散度j加上-log4其实就是C（G）原来的公式，所以得到方程五是没有问题的。并且方程5可以表示为

 我们知道Jensen–Shannon散度是非负的，有且只有他们两相等时才取0，所以我们就得到了最后我们需要证明的东西。

到这里就基本上差不多了。

最后给大家提出一个问题就是，我已开始觉得，最后的最好的结局是生成器G和判别器D达到平衡，生成器G产生的样本以假乱真，判别器能识别出来的概率只有50%，那这样的话，不应该讲生成器完全成功了，而判别器很失败，因为他已经恢复不出真假了，为什么呢？知道的朋友可以在下面留言交流，我之后也许哪天会公布答案。

哈哈，债见。

学术交流可以关注我的公众号，后台留言，粉丝不多，看到必回。卑微小钱在线祈求