最大子序列、最长递增子序列、最长公共子串、最长公共子序列、字符串编辑距离总结

一、最大子序列

即找出由数组成的一维数组中和最大的连续子序列。例如{5, -6, 4, 2}的最大子序列是{4, 2}，它们的和是6。

思路：假设数组为num，用dp[i]存储当遍历到num[i]时，num[0]~num[i]之间求得的最大子序列的和。

遍历num，当遍历到num[i]时，转换方程如下：

如果dp[i-1]>0，则dp[i] = dp[i-1] + num[i]，

否则dp[i] = num[i]。

这么去想，站在num[i]的角度来看，如果dp[i-1]>0，说明前i-1个数的最大子序列和大于0，那么num[i]加上一个正数肯定会比num[i]大，因此dp[i] = dp[i-1] + num[i]。如果dp[i-1]<=0，那么num[i]加上一个非正数肯定比num[i] 小或者相等，所以dp[i] = num[i]

c++代码

#include
using namespace std;
int main(){
	int num[6]={5, -3, -4, 12, 9, -1};
	int len=6;
	int* dp = new int[6];
	int max_len=0;
	if(len>0){
		dp[0] = num[0];
		for(int i=1;i0){
				dp[i] = dp[i-1] + num[i];
			}else{
				dp[i] = num[i];
			}
			if(dp[i]>max_len)
				max_len = dp[i];
		}
	}
	cout<<"最大子序列和为:"<

输出：

最大子序列和为：21

二、最长递增子序列

给定一个长度为N的数组，找出一个最长的单调自增子序列（不一定连续，但是顺序不能乱）。例如：给定一个长度为6的数组A{5， 6， 7， 1， 2， 8}，则其最长的单调递增子序列为{5，6，7，8}，长度为4.

代码：

#include
using namespace std;

int maxLen(int arr[], int length){
    int* dp = new int[length+1];
    int max = 0;
    for(int i=0;idp[i]){
                dp[i] = dp[j]+1;
            }
        }//for
        if(dp[i] > max){
            max = dp[i];
        }
    }//for

    return max;
}

int main(){
    int arr[8] = {1, -1, 2, -3, 4, -5, 6, -7};
    cout<

测试用例：

在序列1，-1，2，-3，4，-5，6，-7中，其最长的递增子序列为1，2，4，6

给定一个长度为6的数组A{5， 6， 7， 1， 2， 8}，则其最长的单调递增子序列为{5，6，7，8}，长度为4

三、最长公共子串和最长公共子序列

最长公共子串（Longest Common Substring）是串的一个连续的部分。最长公共子序列（Longest Common Subsequence，LCS）不一定是连续的，但是不改变序列中元素在原串中的相对顺序，而是从序列中去掉任意的元素获得新的序列。也就是说，子串中字符的位置必须是连续的，子序列则可以不连续。

（1）最长公共子序列

思想

采用动态规划的思想，假设比较字符串s1和s2的最长公共子序列，len1,len2分别为s1和s2的长度，L[m][n]表示当s1[m]和s2[n]比较完之后得到的最长公共子序列长度。有如下转换方程：

如果s1[i] == s2[j]，那么L[m][n] = L[m-1][n-1] + 1；

如果s1[i] != s2[j]，那么L[m][n] = max(L[m-1][n], L[m][n-1])；

 

例子

以腾讯2017年实习生招聘的这道题为例

题目：

构造回文

给定一个字符串s，你可以从中删除一些字符，使得剩下的串是一个回文串。如何删除才能使得回文串最长呢？
输出需要删除的字符个数。

输入描述:

输入数据有多组，每组包含一个字符串s，且保证:1<=s.length<=1000.

输出描述:

对于每组数据，输出一个整数，代表最少需要删除的字符个数。

输入例子:

abcda
google

输出例子:

2
2

思路：

根据回文串的特点，如果一个字符串是回文串，那么这个字符串和它的逆序串是相等的。所以上述问题转化为求字符串和逆序字符串的最长公共子序列长度。

c++代码

#include
#include
#include
using namespace std;
int main(){
	string s;
	while(cin>>s){
			
			string s1=s;
			string s2=s;
			reverse(s2.begin(),s2.end());
			int len1=s1.length();
			int len2=s2.length();
			
			//动态申请一个二维数组
			//因为题目给出了s.length<=1000，因此L的长度可以固定
			//直接定义L[1001][1001]也可以，比动态申请数组更方便 
			int **L = new int* [len1+1];
			int i,j;
			for(i=0; i<=len1;i++){
				L[i] = new int[len2+1];
			} 
			for(i=0;i<=len1;i++){
				for(j=0;j<=len2;j++)
					L[i][j]=0;  //对数组进行初始化 
			}//for
			
			for(i=1;i<=len1;i++){
				for(j=1;j<=len2;j++){
					if(s1[i-1] == s2[j-1]){
						L[i][j] = L[i-1][j-1] + 1;
					}else{
						L[i][j] = max(L[i-1][j], L[i][j-1]);
					}
				}
			}
			
			cout<

例2：

题目描述：怎么判断一个字符串是对称的？如果不对称，求最少需要添加几个元素让其变为对称的？（2017年秋招CVTE面试题）

思路：对称其实就是回文，第一问简单就不说了，第二问和上面例子其实差不多，对于一个不对称的字符串str，求它与它的逆序的最长公共子序列x，然后用长度len-x，即为要添加的元素数

（2）最长公共子串

思路和最长公共子串差不多，也是用动态规划的方法。唯一要改变的一个地方是转换方程那，改成：

如果s1[i] == s2[j]，那么L[m][n] = L[m-1][n-1] + 1；

如果s1[i] != s2[j]，那么L[m][n] = 0；

因为要求是连续的，因此只要有一个不相等的出现，那么就把L[m][n]置为0。

例子

来源：2017年校招全国统一模拟笔试(第二场)编程题集合-牛客网

链接：https://www.nowcoder.com/questionTerminal/276712b113c6456c8cf31c5073a4f9d7

时间限制：1秒空间限制：32768K

题目描述：

牛牛有两个字符串（可能包含空格），牛牛想找出其中最长的公共连续子串，希望你能帮助他，并输出其长度。

输入描述：

输入为两行字符串（可能包含空格），长度均小于等于50.

输出描述：

输出为一个整数，表示最长公共连续子串的长度

实例1：

输入

abcde

abgde

Sit it out G
Sit down and shut up

输出

2

4

代码：

#include
#include
#include
#include
#define MAX 55

using namespace std;

int dp[MAX][MAX];

int main() {
    char str1[MAX], str2[MAX];
    int len1, len2;
    while(cin.getline(str1, MAX)){
        cin.getline(str2, MAX);
        memset(dp, 0, sizeof(dp));
        len1 = strlen(str1);
        len2 = strlen(str2);
        if(len1 == 0 || len2 == 0){
            return 0;
        }//if
        int i,j,max_len=0;
        for(i=1;i<=len1;++i){
            for(j=1;j<=len2;++j){
                if(str1[i-1] == str2[j-1]){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }
                if(dp[i][j] > max_len){
                    max_len = dp[i][j];
                }
            }//for
        }
        cout<

这道题要注意的是输入的字符串可能包含空格！！！因此不能用string了，要用char数组结合cin.getline函数。

四、字符串编辑距离

编辑距离，又称Levenshtein距离，是指两个字符串之间，由一个转成另一个所需的最少编辑操作次数。

允许的操作包括（1）删除一个字符（2）插入一个字符（3）将一个字符改为另一个字符

利用动态规划的思想。用一个二维数组edit[i][j]，表示第一个字符串s1的长度为i的子串和第二个字符串s2的长度为j的子串的编辑距离。那么容易得到如下的转化方程：

if i==0 且 j==0, edit(i,j) = 0

if i==0 且 j>0, edit(i, j) = j

if i>0 且 j==0, edit(i,j) = i

if i>0 且 j>0, edit(i,j) = min{ edit(i-1,j)+1, edit(i, j-1)+1, edit(i-1,j-1)+diff(i,j)}

其中diff(i,j)表示的是s1[i] 和s2[j] 是否相等，如果s1[i] == s2[j]，那么diff(i,j)=0，否则diff(i,j)=1

举个栗子：

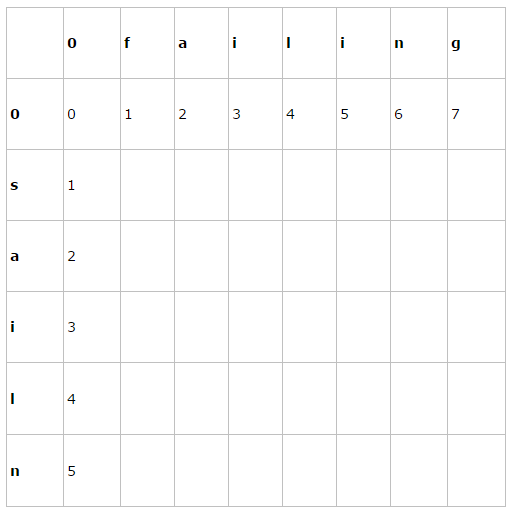
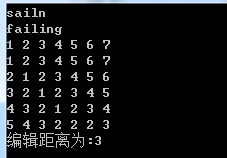
假设s1 = "sailn"，s2="failing"，len1,len2分别为s1和s2的长度，为了处理边界的情况，一般在动态申请二维数组edit的时候多申请一行和一列，变为edit[len1+1][len2+1]。

那么初始化情况如下：

edit从[1][1]开始算，但是注意比较的s1和s2是从下标0开始。明白了思想后，写出代码不难。

c++代码如下：

#include
#include
using namespace std;
int main(){
	string s1,s2;
	int i,j;
	//比较s1和s2的编辑距离
	while(cin>>s1>>s2){
		int len1=s1.length();
		int len2=s2.length();
		
		if(len1==0 && len2==0){
			cout<<0<0){
			cout<0 && len2==0){
			cout<

输出如下：