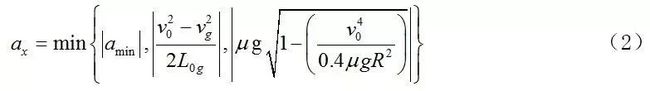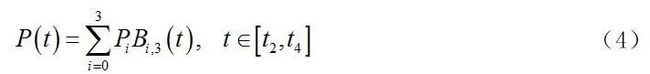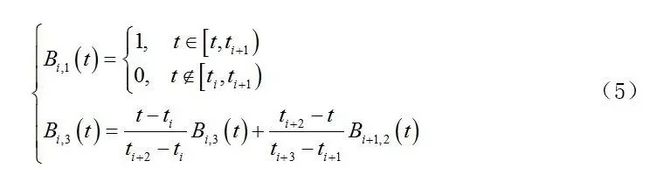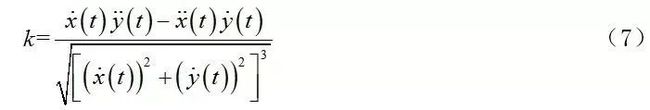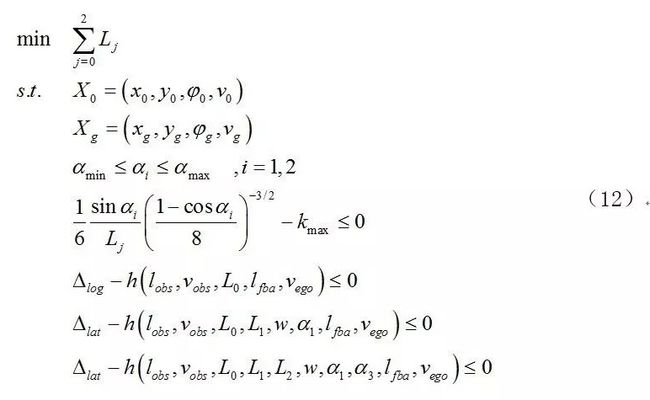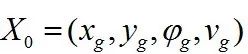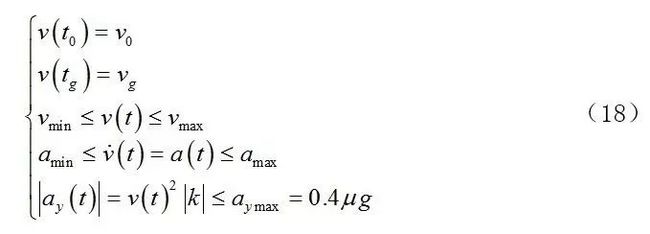编者按：运动规划作为一种具有多个非线性约束的高维优化问题，需要消耗大量的计算资源，并且由于场景的复杂性和实时性，不是总能快捷简单的得到最优轨迹，这对规划算法的鲁棒性和实用性有着较高的要求。本文提出了一种轨迹监控策略，同时进行换道轨迹规划和监控轨迹规划，在前者未能规划出轨迹或者规划超时，系统将以监控轨迹作为输出，保证车辆换道的稳定性和可行性。为满足车辆运动约束以及实时性要求，将采用基于B样条的方法来规划连续曲率路径。基于RRT的方法可以作为保持算法完备性的补充。然后，监控轨迹主要遵循无碰撞要求，通过减速规划以保持车辆实时运动的稳定性。
本文译自《A Novel Robust Lane Change Trajectory Planning Method for Autonomous Vehicle》，文章出自会议IV2019，作者为来自同济大学智能汽车研究所的熊璐教授、曾德全博士等。
摘要：本文提出了一种新颖的自动驾驶车辆的换道轨迹规划方法。由于难以准确地获得其他车辆的运动轨迹，自动驾驶车辆的运动轨迹不能总是快速简单的得到。此外，运动规划作为一种具有多个非线性约束的高维优化问题，需要大量计算资源才能找到正确的解决方案。为此，我们提出了一种轨迹监控策略，同时进行换道轨迹规划和监控轨迹规划，保证车辆换道的稳定性和可行性。在前者未能规划出轨迹或者规划超时，则系统将以监控轨迹作为输出。为满足车辆运动约束以及实时性要求，将采用基于B样条的方法来规划连续曲率路径。基于RRT的方法可以作为保持算法完备性的补充。然后，监控轨迹主要遵循无碰撞要求，通过减速规划以保持车辆实时运动的稳定性。结果表明，基于B样条的方法和基于RRT的方法都可以产生曲率连续路径并满足运动限制，但两者都有可能超时。特别是，随着环境变得更加复杂，成功率也面临挑战。
1. 引言
近几十年来，自动驾驶技术作为一种前景广阔的技术取得了良好的发展，并已经有大量的技术产品投入应用[1-3]。 与人类相比，智能驾驶系统由于其快速操作，超出视觉范围的感知和准确的决策，有望提高驾驶安全性，舒适性，交通效率和能源经济性[4-6]。
为了安全快速地将智能车辆从当前位置导航到目标点，必须设计一种用于生成轨迹的鲁棒性高的运动规划方法[7]。如文献 [1-2]所述，运动规划架构主要包括基于图搜索的规划方法，基于采样的方法，插值曲线规划法和数值优化法。Dijkstra [8]和A * [9]是基于图表搜索的较常见的规划方法。先将环境离散化之后，通过遍历网格找到最短路径，无论网格是相同大小[10]还是可变粒度[11]。尽管智能车中使用的算法有很多变种，如D * [12]，ARA * [13]，AD* [14]，但仍然很难选择网格分辨率并跟踪由连接网格组成的路径[15]。与离散的环境方法不同，基于采样的规划方法（如RRT [16]）可以通过在连续空间中扩展节点直到达到目标位置来产生有效路径。应用于智能汽车的算法的最新变体是RRT * [17]和CL-RRT [18]，但是，此类规划的结果不是最优的，生成的路径曲折并且由于随机采样的原因，使得车辆难以直接进行轨迹跟踪。插值曲线规划方法能够实现曲率连续性，如多项式曲线[19]，回旋曲线[20]，贝塞尔曲线[21]和B样条[22]，它需要在一组给定的路径点基础上来拟合出一条新的路径。由于自动驾驶车辆的场景是实时动态的，因此难以遍历所有环境以获得路径点。通过构建障碍约束，起点约束，目标点约束，模型约束和优化目标函数（例如，最短路径和最舒适等约束），数值优化[23-25]可以在没有路点的情况下规划最佳平滑轨迹。然而，这种方法本质上是一种具有多个非线性约束的高维优化问题，需要大量资源才能找到正确的解决方案。文献[26-27]表明，为了产生满足多目标约束的泊车轨迹，CPU时间通常不小于300ms，甚至40000ms。此外，还有规划失效的可能性[15]。
为了提高运动规划算法的鲁棒性，避免无路可走的困境，我们提出了一种轨迹监控策略，同时产生换道轨迹和监控轨迹。如果前者没有产生安全轨迹或超时，则监控轨迹将作为结果输出。否则，输出是换道轨迹。为了满足车辆运动的约束和实时规划的要求，将采用基于B样条的方法来规划车道变换的连续曲率路径。并且基于RRT的方法作为保持车道变换计划算法的完整性的补充。然后，监控轨迹主要遵循无碰撞要求，通过减速规划以保持车辆稳定性。本文的其余部分结构如下：在第二部分，描述了一种轨迹监控的策略。第三部分描述了基于B样条的换道路径规划方法。第四部分描述了基于RRT算法的换道轨迹规划方法。第五部分描述了速度规划方法。第六部分实现并分析了典型车道变换场景的轨迹规划算法。最后，第七部分介绍了本文的结论。
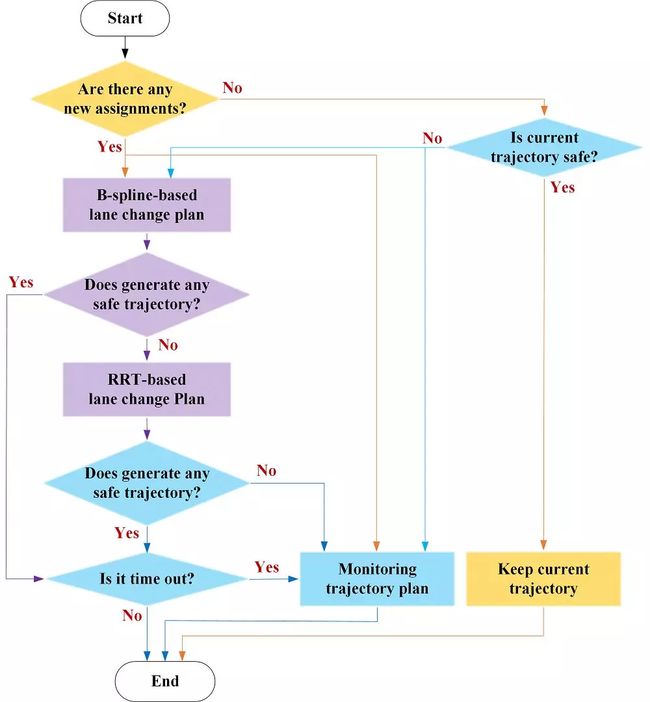
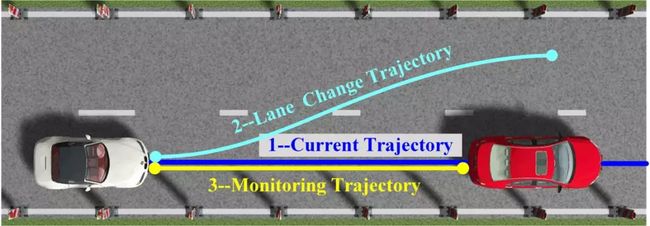
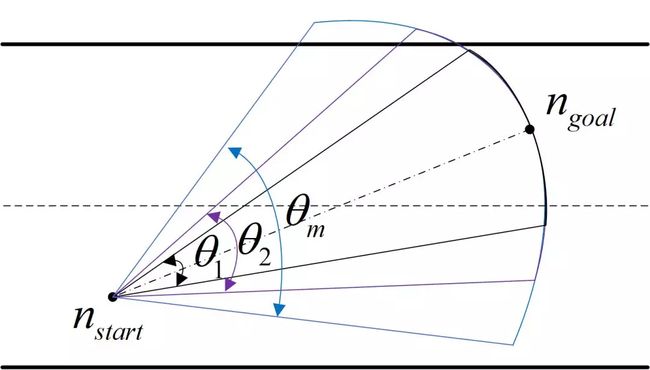
通常情况下，难以准确地掌握周围车辆的运动轨迹，这意味着自动驾驶车辆的换道轨迹并不总是容易快速获得。而且，运动规划的本质是一种具有多个非线性约束的高维优化问题，需要大量的资源才能找到正确的解。因此，规划并不是总能够得到正确的路径。为了避免碰撞，有必要建立一个安全策略，就像车辆组件的功能安全一样，可以在必要时提供最安全的轨迹。因此，我们提出了一种轨迹监控策略，如图1所示，用于车道变换场景。如果驾驶任务保持不变且当前轨迹安全，则应保持当前轨迹。相反，换道轨迹和监控轨迹将同时开始规划。如图2所示，通过基于B样条和基于RRT的方法生成车道变换轨迹（No.2的浅蓝色曲线），并且在减速时生成监视轨迹（No.3的黄线） 。如果前者没有生成安全轨迹或超时，则监监控轨迹将作为结果输出。否则，输出的是换道轨迹。
图1 轨迹监控策略
图2 换道场景1
尽管监控轨迹具有与AEB类似的效果，但它比AEB更“智能”。如图3所示，当车辆改变车道时，路边防撞桩进入车辆感知区域（最短距离将小于车道宽度），其已达到触发AEB的条件。但是，车辆执行的车道变换轨迹应该是安全的，并且AEB不应该介入。
图3 换道场景2
如果监控轨迹的减速度为αx，则为直线行驶
其中αmin是车辆最小加速度，V0是初始速度，Vg是目标速度，L0g是减速长度。
如果转弯半径为R，对于直线驾驶而言
其中μ是路面附着系数。
2. 基于B样条曲线的换道轨迹规划方法
A. 问题定义
一般来说，路径规划问题可以被定义为典型的两点边值问题，
其中f(x)是目标函数，通常用最短时间或者路程来描述代价，gi(x)代表起始点和目标点的约束，hj(x)代表安全距离约束。
B.曲率约束
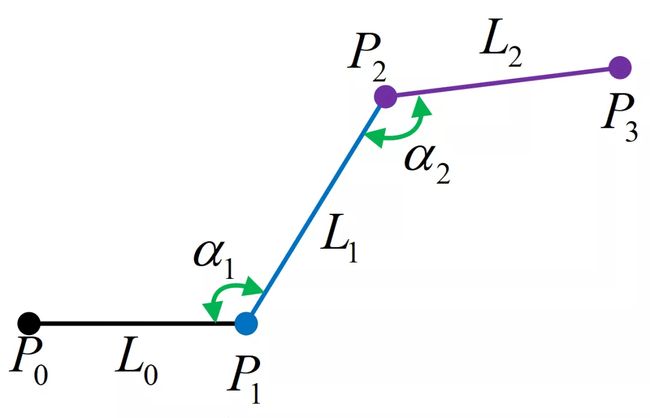
为了满足车辆转向执行器的限制，生成的路径应该满足连续曲率，峰值曲率和最大曲率的约束，采用参数化的三次B样条曲线来规划路径，如图4所示。
图4 三次B样条曲线的控制点
图4中具有4个控制点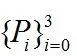
和7个参数节点
的三次B样条曲线能够被定义为
其中Bi,j代表B样条曲线的基函数，可以通过deBoox-Cox公式递推得到。
为了满足起点和目标点的约束，顶部和底部的端点需要设置为三个节点，因此参数节点的矢量将设置为[0,0,0,0,0.5,1,1,1,1], 然后，通过等式（6）分别描述通过三次B样条生成的路径点的表达式。
曲率表达式如式（7），
由控制点构成的控制线段如图4所示。为了满足车辆的峰值曲率约束，控制线的长度和夹角受式（8）[28]的约束。
C.安全距离约束
基于b样条曲线的凸特征，可以通过控制段与障碍物之间的距离来表示生成路径的安全检测。典型情况如图5所示。
图5 安全检测
根据自我车辆的位置，存在三个阶段发生碰撞风险，其中需满足各自的安全约束条件。假设自动车辆的避障是通过强制转向而不是改变速度来实现的，其目的在于使乘客感到舒适。 因此，详细安全性检测如下：
⑴第一个控制段L0的纵向安全距离
⑵第二个控制段L1的横向安全距离
⑶第三个控制段L2的横向安全距离
其中，lfba是自车从后轴到头部的长度，w是自车宽度，Δlog是横向安全距离，Vego是自车速度。
最后，路径规划这样一个两点边值问题可以被定义为;
其中
代表起始点，
代表目标点。
公式（1）和（10）说明智能车辆的路径规划是具有多个约束的线性规划问题。但是，约束主要是非线性的。处理这类问题主要有三种方法：离线数据集方法，凸优化和仿生智能优化算法。由于智能车辆的环境难以穷尽，许多离线数据存储，提取和匹配需要大量的计算资源，离线数据集方法的应用受到限制。由于凸优化方法要求域是凸的，环境中的所有障碍必须用广义仿射集的形式表示，它加剧了环境地图的处理要求，使其难以应用于高速动态环境中。与上述求解方法相比，仿生智能优化算法由于对定义域，函数组成和优化函数的环境描述要求较低，非常适合解决高维非线性优化问题，并已广泛应用于运动规划中[29]。经过不断的尝试，我们最终选择了蚁群算法来解决路径规划问题。
由于由公式（10）建立的优化问题严格地限制了曲率，并且蚁群解算法的局部最小值问题使得算法失去其完备性。因此，当基于B样条的算法没有解决方案但路径存在时，添加基于RRT的算法以尽可能地找到路径。当然，为了加快算法的求解速度，引入了一些措施来减少采样的盲目性，如高斯采样，自适应采样空间和最近邻搜索策略。同时，为了解决原始RRT规划结果包含大量曲折路径导致曲率不连续的问题，采用样条曲线的平滑处理方法使规划结果能够由智能车辆执行。
A.高斯采样策略
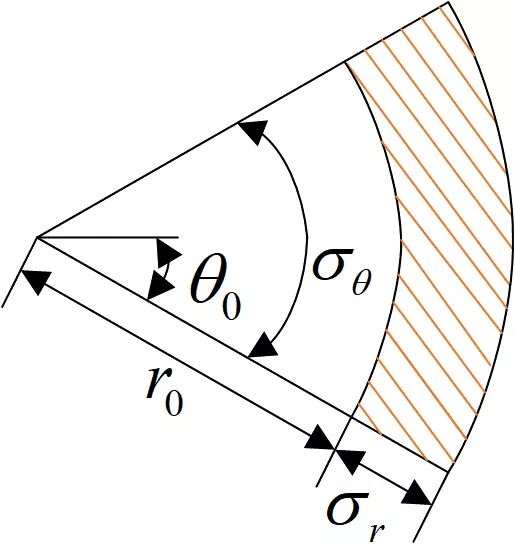
随机采样函数是基本RRT的传统采样方法，这意味着配置空间中每个点的扩展概率相等。 但是，考虑到汽车最小转弯半径的限制，机车前方的扩展概率应高于后方。因此，高斯采样将与实际驾驶行为更加一致。如图6所示，采样节点位于扇形的阴影区域。
图6 高斯采样概率分配
根据公式：
其中（Sx,Sy）是采样节点，（X0,Y0）是参考节点，（r,θ）是高斯参数，可通过式(14)得到。
其中（r0,θ0）是偏移参数，（σr,σθ）代表高斯标准差，（rrand,θrand）是随机参数。
B.自适应采样空
采样空间越小，到目标点的扩展越快。但是，这可能使得无法在复杂环境中扩展到目标点。为了提高算法对环境的适应性，在公式（15）中定义的偏移角θ中引入成功因子ε(ε>0)。
成功因子 可以根据环境的复杂性，以及先前扩展的成功率和扩展的数量自适应调整。公式（15）采用了近似的方法，因为最大特征空间是矩形图而不是360度圆。
图7 自适应采样空间
C.最近邻域搜索方法
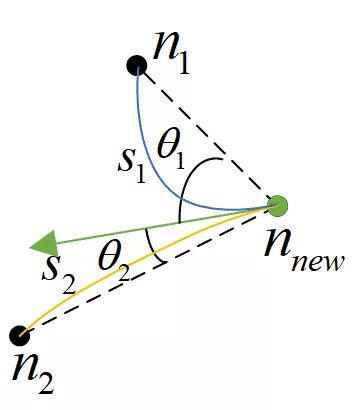
放入RRT树的新节点应该在采样后链接到RRT路径树中最近的节点。通过邻域搜索算法寻找最近的节点，并使用经典的欧几里德距离作为度量。然而，由于车辆最大转向角的约束，两个节点之间的转向角也应被视为较小的角度，意味着更平滑的路径。如图8所示，根据欧几里德距离，节点n1是新采样节点n的最近节点。然而，从节点 到节点n1的转向角更大，导致路径s1连接 和n1更为尖锐。为了使路径更利于车辆跟踪，由式（16）定义的传统度量函数被修改为式（17）。
图8 度量示意图
4. 速度规划
在路径生成后，应根据边界约束（如起始速度和目标速度），执行器约束（如最大速度和最大加速度）和稳定性约束（最大侧向加速度）计算速度曲线，如下所示：
利用三次多项式曲线描述速度曲线：
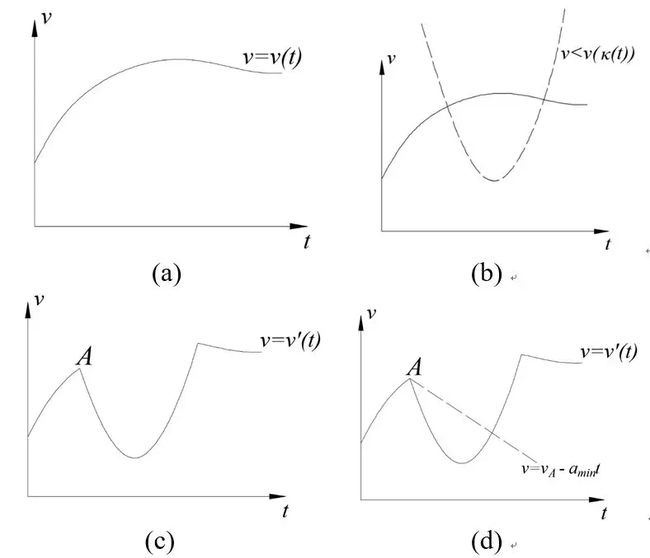
首先，基于起始速度和目标速度，速度分布如图9（a）所示。其次，根据图9（b）所示的最大侧向加速度限制（虚线），可以得到如图9（c）所示的速度曲线。最后，结合加速度极限，可以得到最终速度曲线，如图9（d）所示。
图9 速度规划
5. 实验结果和分析
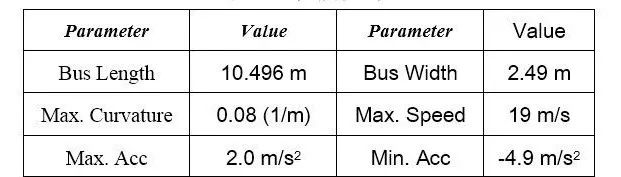
模拟在C ++ 11 / Linux中进行，并在Jetson TX2上执行，Jetson TX2在HMP Dual Denver 2/2 MB L2+QuadARM®A57/ 2 MB L2上运行。车辆参数列于表I.
表1 车辆参数
A.基于B样条曲线的换道轨迹规划
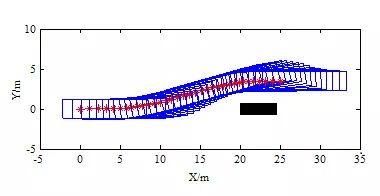
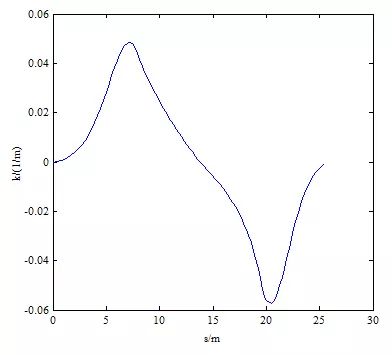
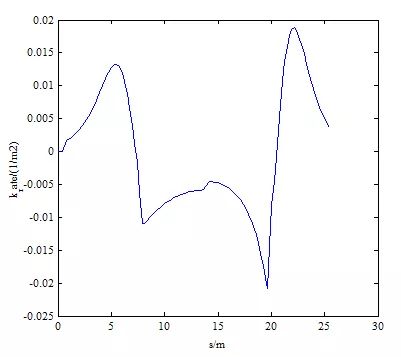
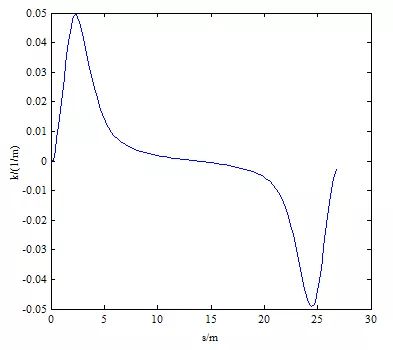
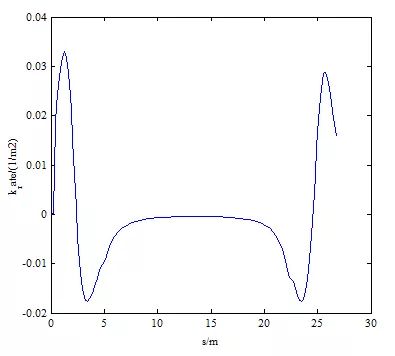
车道变换的场景1如图10所示，起点为（0,0,0,15），目标点为（25,3.5,0,10）。静止障碍物位于（20,0.7），长4.5米，宽1.4米。轨迹的曲率是连续的，如图11所示，其最大值为0.05729 / m（小于0.08 / m的限制），曲率率小于0.02 / m2，如图12所示。
图10 换道方案1
图11 换道方案1规划路径曲率
图12 换道方案1规划路径曲率变化率
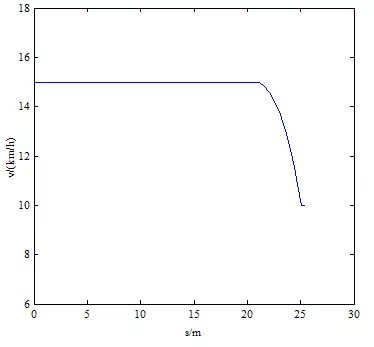
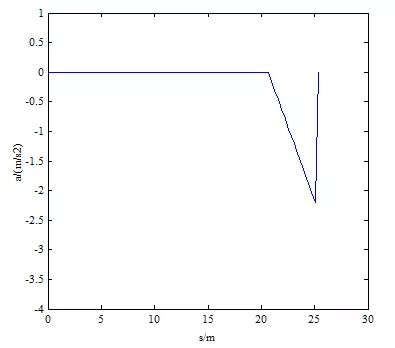
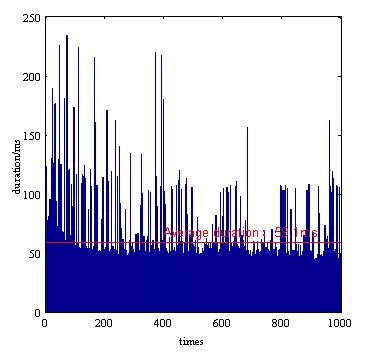
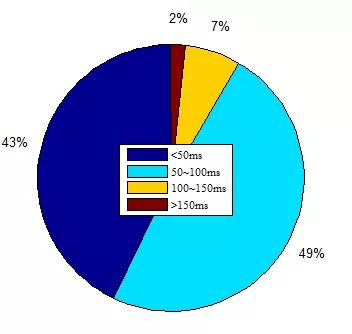
如图13所示，速度分布是连续的，最小加速度小于2.20 m / s2（满足小于4.9 m / s2的限制）。为了更好地分析计划的时间性能，我们总共进行了1000次滚动计算。虽然轨迹生成的平均持续时间是59.1ms（小于我们100ms的目标），但是仍然有足够的时间超过100ms，甚至高达250ms，如图15所示。并且如图16所示，生成持续时间的概率为9％超过100ms。但车道变换的所有轮廓意味着基于B样条的方法可以产生连续的曲率并满足运动的限制。
图13 换道方案1速度曲线
图14 换道方案1加速度曲线
图15 换道方案1的规划时间
图16 换道方案1的规划时间分布
B. 基于RRT的换道轨迹规划
车道变换的场景2如图17所示，起点为（0,0,0,15），目标点为（25,3.5,0,10）。RRT的停止标准是 并且最大迭代次数不超过1500.静态障碍物位于（17,0.7），长度为4.5m，宽度为1.4m。
图17 换道场景2
图18 换道方案2规划路径曲率
图19 换道方案2规划路径曲率变化率
图20 换道方案2的速度规划
图21 换道方案2的加速度曲线
图22 换道方案2的规划时间
图23 换道方案2的成功规划时间
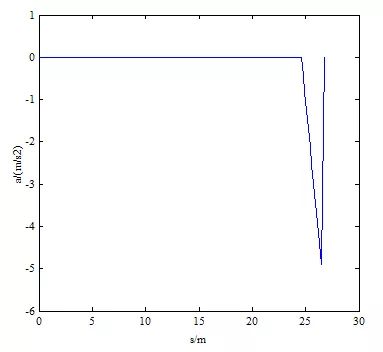
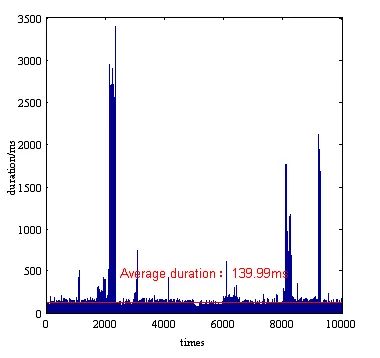
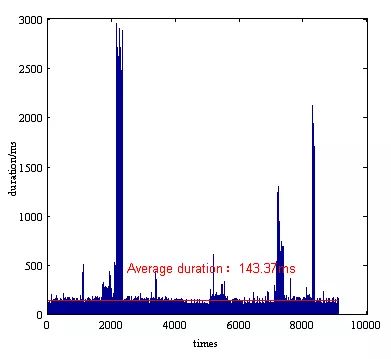
如图18所示，轨迹的曲率是连续的，其最大值为0.050 / m（小于0.08 / m的限制），曲率率小于0.033 / m2，如图19所示。如图20所示，速度分布是连续的，最小加速度非常接近4.9 m / s2的限制。如图22所示，所有轨迹生成的平均持续时间为139.99ms（超过我们100ms的目标），并且有足够的时间超过100ms，甚至高达3500ms。如图23所示，对于成功规划，所有轨迹生成的平均持续时间为143.37ms（超过我们100ms的目标），并且有超过100ms的多种时间，甚至高达3000ms。
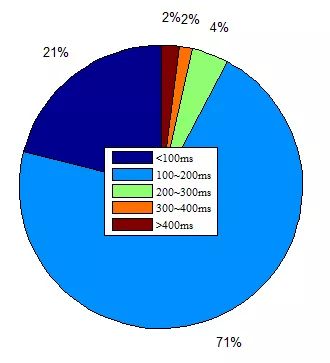
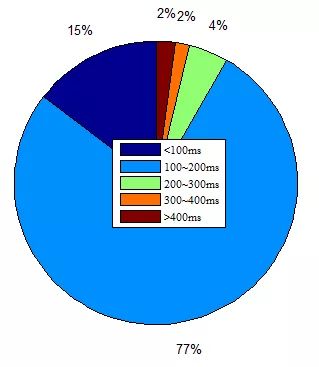
为了更好地分析计划的时间性能，我们总共进行了10000次滚动计算。并且如图24所示，规划时间仅有21％的概率满足小于100ms的要求。产生小于200ms的轨迹的可能性为92％。但是在规划成功的前提下，时间小于100ms的次数减少到15％，如图25所示，尽管在200ms内规划完成的概率只有92%，但是成功率达到了91％。此外，所有基于RRT的方法的换道曲线可以产生连续的曲率并满足运动的限制。
图24 换道方案2的所有规划时间分布
图25 换道方案2的成功规划时间分布
图26 换道方案2的成功率
6结论
为了提高运动规划算法的鲁棒性，避免了无路可走的困境，本文提出了一种新的自动驾驶车辆换道轨迹规划方法。我们提出了一种轨迹监控策略，在换到过程中保持稳定性的同时生成换道轨迹和监控轨迹。如果前者没有规划出安全轨迹或者规划超时，则监控轨迹将作为结果输出。否则，输出是换道轨迹。为了满足车辆运动和实时要求的约束，将采用基于B样条的方法来规划换道的连续曲率路径。并且基于RRT的方法作为保证换道规划算法的完备性的补充。然后，监视轨迹主要遵循无碰撞要求，其计算减速度以保持车辆稳定性。结果表明，基于B样条的方法和基于RRT的方法都可以产生连续曲率并满足运动限制，但两者都有可能超时。特别是，随着环境变得更加复杂，成功率也面临挑战。未来的工作将集中在真实的车辆实施和测试上。如果我们努力研究更强大的功能安全策略，收获可能不小。