算法设计技巧-贪婪算法、分治算法、动态规划等
1.贪婪算法(greedy algorithm)
贪婪算法的核心思想是将问题分阶段进行,在每个阶段选择当前最优的,而不考虑对之后的影响。这意味着选择是局部最优的,我们希望贪婪算法结束时我们希望局部最优等于全局最优,否则得到的只是次最优解。一个典型的问题是货币找零问题,假设现在有面值10元,5元,1元的钞票,要选出最少的钞票组成23元,那么方法是,从面值最大的开始重复选取,直到超过所要组成的面值。从而23元的最少找零方法是,10,10,1,1,1。
贪婪算法的主要应用有:简单的调度问题,文件压缩编码(哈夫曼编码),贪婪近似问题(背包,装箱问题)。
1.1 单线简单任务调度问题
简单调度问题是指,无重复任务,且当某个任务执行时,直到执行完该任务才可执行其他任务。任务调度问题可分为单线与多线,指可同时处理的任务数。假设有作业ji,完成作业所用的时间ti,i[1,N]。如何确定作业的执行顺序,使作业完成时刻的平均值最小。例如 j1=1,j2=8,j3=3,。假设从时刻0开始,一个作业没有执行先后顺序,对于两个作业,如j3=3和j2=8,不管执行顺序如何,所有任务执行完的时刻是相同的,均为11。只有当一个任务执行完后才可以执行其他任务,因此对于两个任务,全部执行完的时刻相同,均为j3+j2=11,先选取j3执行,那么j3执行完的时刻为3;先选取j2执行,那么j2执行完的时刻为8,因此先执行所用时间少的j3符合要求,同理,将两个任务的情况向后推广。很明显,先执行所用时间少的任务,使得当前的平均任务完成时刻最小,因此每次都执行当前剩余执行任务中,所用时间最少的那个任务。所以对所有待执行的任务ji增序排序,依次执行所用时间小的任务,最后可得到最小的平均作业完成时刻。(书籍中的表述有歧义,因此无论如何安排执行任务,每个任务所用时间是不变的,因此完成所有任务的平均时间也一定是相同,t=sum(ji)/N,但是通过调度,可以使得所有任务完成时刻的平均值最小)
因此平均完成时刻=总完成时刻/任务数,所以令当前总完成时刻最小的任务也令平均完成时刻最小。选取第一个时,令当前平均完成时刻最小的是J1,J=1,选取J1;选取第二个时,令当前平均完成时刻最小的是J2,J=1+9,同理可推广至N。
1.2 多线简单任务调度问题
1.2.1 平均完成时刻最小化
假设有N个不同的任务ji,有m(m>1)个处理器,那么可同时处理m个任务,如何安排任务的执行顺序使得总的平均完成时刻最小呢。方法同单线简单任务调度,但是因为多个处理器,因此在按照执行时间增序排序任务后,按照处理器个数分成m组,每组任务同时在m个处理器上完成,但是那个任务在哪个处理器上完成并不影响最终的平均完成时刻。
1.2.2 最早完成时刻
最早完成时刻的多线简单任务调度问题,实际上转换为了装箱问题,因此要保证的是,在每个处理器上,最后一个任务完成的时刻ti的最大值最小,才能保证所有处理器的完成时刻最早。
1.3 有冷却期的单线多任务调度问题
Leetcode621. Task Scheduler https://leetcode.com/problems/task-scheduler/
c++实现
https://github.com/AnkangH/LeetCode/blob/master/%E8%B4%AA%E5%BF%83%E7%AE%97%E6%B3%95/621.%20Task%20Scheduler.cpp
题目:给定一个字符序列,字符从'A'-'Z'代表不同任务,及一个正整数n,代表相同任务的冷却期,冷却期内只可执行不同任务,当没有不同任务可执行时,执行idle,假设每个任务执行时间相同都为1,判断执行完所有任务所需的最少时间。
基于题目的要求,出现次数最多的任务,消耗的idle(非必要时间)越多,因此优先执行出现次数多的任务。同时由于冷却期的存在,当冷却期结束时,要再次执行上述判断。例如 'A'任务x3,'B'任务x1,'C'任务x1,'D'任务x1,n=2,首先执行A任务,顺序执行次数相同的,BC,此时A任务的冷却期结束。若仍然顺序执行任务D,那么剩余5个任务A至少需要3x5=15个任务执行时间才能执行完毕,总时间为4+15=19。而如果在冷却期结束后,优先执行任务数目多的A,那么执行完ABCAD之后,执行剩余的4个A任务只需要4x3=12个任务执行时间,总时间5+12=17。从上述分析可知,每一轮以n+1为限,以当前待执行次数降序执行任务,更新当前轮执行任务的剩余执行次数,如果不够n+1则以idle补足n+1。继续程序直至没有所有任务的待执行次数为0。注意在最后一轮时,如只剩A任务需执行一次,那么不需以idle补足n+1,因为之后没有任务需要执行。
上述算法存在两种实现方法。一是使用序列保存待执行次数,每轮执行前降序排序序列,选取待执行次数多的任务,更新剩余执行次数。二是使用大顶堆(优先队列),利用堆的最大值属性和出堆进堆操作,获取降序序列,需注意堆顶元素处理后需出堆,防止一轮中重复选取任务,一轮处理结束后,更新过的任务剩余执行次数再入堆。使用堆的时间复杂度更优,因为不需要重复排序,使用快排的sort,时间复杂度为O(NlogN),而堆的插入和删除只需要O(logN)的时间复杂度。
1.3.1 重复排序方法
这里实现的时候想的复杂了,其实不需要哈希表和自定义排序序列,因为只关心任务待执行次数即可,使用一个vector
class Solution {
public:
int leastInterval(vector& tasks, int n) {
unordered_map taskMap;//每个字符出现的次数
int sizeTask=tasks.size();
for(int i=0;i> mapOrder;//保存任务数降序排序的任务序号
//保存任务降序序号
for(int i=0;i<26;i++)
{
if(taskMap.count(i+'A')!=0)
mapOrder.push_back(pair{i+'A',taskMap[i+'A']});
else
mapOrder.push_back(pair{i+'A',0});
}
//降序排序
sort(mapOrder.begin(),mapOrder.end(),cmp);
int res=0;//记录程序总运行时间
while(taskMap.size()!=0)
{
int size=0;
for(int i=0;i<26;i++)//每一轮选取
{
if(taskMap.count(mapOrder[i].first)!=0)//从次数多的开始选取
{
size++;//记录本轮已执行任务
taskMap[mapOrder[i].first]--;//更新剩余执行次数
if(taskMap[mapOrder[i].first]==0)
taskMap.erase(mapOrder[i].first);//当剩余执行次数为0时,删除该任务
if(size==n+1)//到达冷却时间 退出本轮
break;
}
}
if(size{i+'A',taskMap[i+'A']});//剩余待执行次数入队列
else
mapOrder.push_back(pair{i+'A',0});
}
sort(mapOrder.begin(),mapOrder.end(),cmp);//排序 剩余执行次数多的在前 优先执行
}
return res;
}
static bool cmp(pair a,pair b)
{
return a.second>b.second;//以pair的第二个参数 降序排序
}
};
1.3.2 大顶堆(优先队列)方法
class Solution {
public:
int leastInterval(vector& tasks, int n) {
vector taskCount(26,0);//每个任务出现次数初始化为0
int res=0;//总执行时间
//0-‘A’ 15-‘Z’
for(auto p:tasks)
taskCount[p-'A']++;//记录每个任务的执行次数
priority_queue heap;//大顶堆
for(auto p:taskCount)
if(p!=0)
heap.push(p);//待执行次数不为0的每个次数入堆
vector temp;//记录出堆的任务剩余待执行次数
while(!heap.empty())//堆空代表所有任务都执行完
{
int size=0;//记录本轮执行的任务数
for(int i=0;i<=n;i++)//每轮的冷却时间 保证冷却时间过后 数目最多的优先执行
{
if(!heap.empty())//检查堆非空
{
int cur=heap.top()-1;//取当前待执行次数最多的任务执行 更新剩余待执行次数
if(cur!=0)
temp.push_back(cur);//仍需执行的次数暂时保存
size++;//本轮已执行的任务数目
heap.pop();//执行完堆顶任务后,堆顶任务出堆,防止在一轮中重复选取
}
}
if(!temp.empty())//有待执行任务
{
for(auto p:temp)
heap.push(p);//待执行任务的待执行次数入堆
temp.clear();//清空待执行任务序列 为下次保存做准备
}
if(size 1.4 Trie树及哈夫曼编码
1.4.1文件压缩
考虑在标准ASCII码中,有100多个可打印的字符。为了区分这些字符,常规使用的是二进制的方法,通过二进制一位的不同而区分不同的字符,因此100个字符至少需要log100向上取整为7个比特位(二进制位),因此如果想表示的集合有C个不同元素,那么至少需要LogC向上取整个比特位。
考虑如何降低比特位的数目,假设一个文件中出现的字符频率是大尺度不同的,因为编码数目有限,那么对于出现频率高的字符,定义短的编码,而出现频率低的字符,定义长的编码,这样储存空间和总的传输时间都会大大降低。因此只有当字符的频率不同时才可以进行文件压缩。
对文件压缩的方法是采用二叉树方法,从根节点出发,往左走为0,往右走为1,直到到达叶节点,到达叶叶节点的路径被定义为叶节点对应字符的编码,这种数据结构称为Trie树。只要保证所有字符都在叶节点上,那么就不会有二义性(即代码与字符是单映射)。字符代码的长度是否相等不重要,只要该字符代码没有其他字符代码的前缀即可。如010代表a,那么0和01一定不能是某个字符的编码。
1.4.2 哈夫曼编码
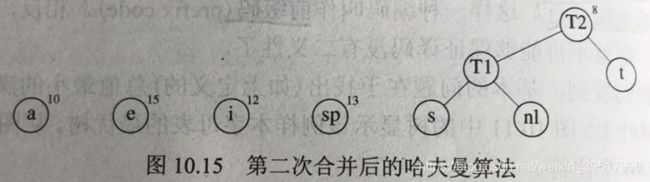
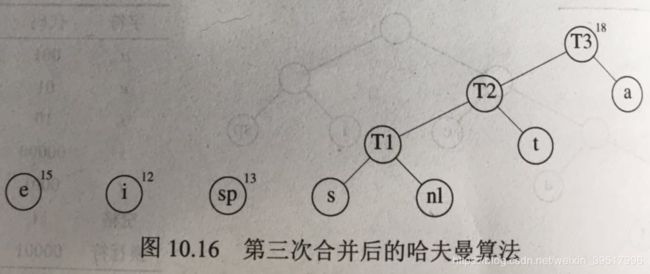
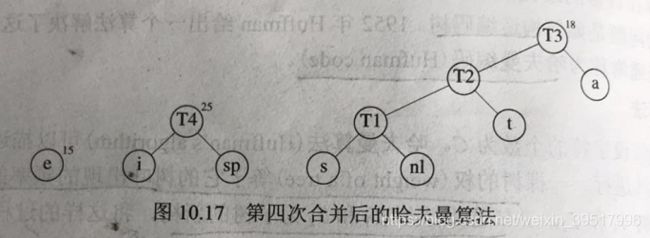
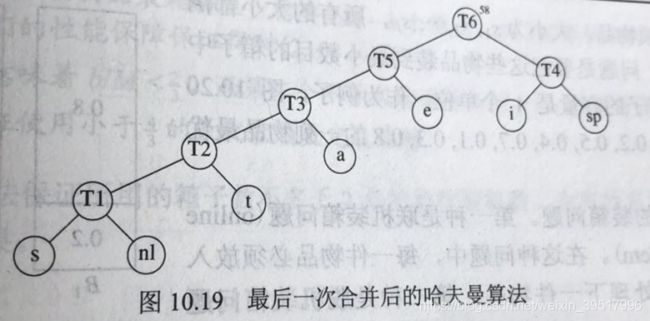
哈夫曼给出了上述Trie树的构造方法,因此也称哈夫曼编码。哈夫曼算法的定义是:算法对由树组成的森林进行。一棵树的权等于它的树叶出现的频率和。任意选取两个权最小的树T1和T2,任意形式组成一棵新树T,(T1和T2都是T的子树,但不限定左右),将这样的算法进行C-1次,直到森林中只有一颗树。算法的起点是所有单节点的树组成的森林,每棵树只有一个节点,节点值为该字符,权为该字符的出现频率。
在相同深度上交换任意两个节点所代表的字符不影响最优性,因而哈夫曼编码树不是唯一的。该算法是贪婪算法,因为每次构建树时,都是选取当前权最小的两个树,而没有考虑全局影响。如果使用优先队列来实现,那么时间复杂度是O(CLogC),若队列由链表实现,则时间复杂度为O(C*C)。
文件经哈夫曼算法压缩后必须提供编码信息,否则由于哈夫曼的两个任意性,文件将不可译码。其次,哈夫曼算法中有一个参数是频率,因此必须先对输入进行一次扫描记录频率信息,第二次扫描才能完成编码。
1.4.3 哈夫曼编码C++实现
c++源代码 https://github.com/AnkangH/CSDN/blob/master/Trie/trie&huffman.cpp
构建哈夫曼编码树
//cout语句只为显示过程 可删去
TreeNode* huffmanCode(const vector>& file)
{
int sizeFile = file.size();
//小顶堆 以权降序排序节点
priority_queue,vector>,greater<> > que;
//构造节点并入堆
for (int i = 0; i < sizeFile; i++)
{
TreeNode* temp = new TreeNode(file[i].second, file[i].first);
que.emplace(temp->weight, temp);
}
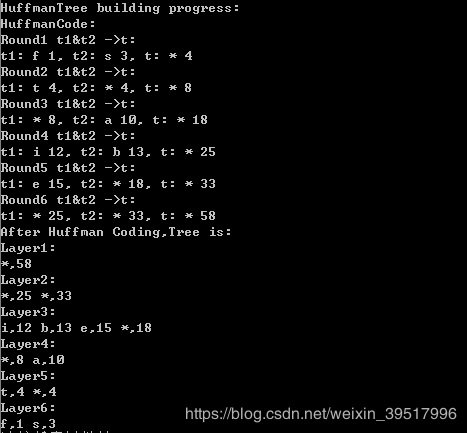
cout << "HuffmanCode:" << endl;
int count = 1;
//因为两个节点合并成一个节点 因而最后堆中只剩一个节点
while (que.size() > 1)
{
auto p = que.top();
TreeNode* t1 = p.second;
que.pop();//最小的出堆
p = que.top();
TreeNode* t2 = p.second;
que.pop();//第二小的出堆
cout << "Round" << count << " t1&t2 ->t:" << endl;
count++;
//合并权最小的两个树
TreeNode* t = new TreeNode('*', t1->weight + t2->weight);
cout << "t1: " << t1->val << " " << t1->weight << ", t2: " << t2->val;
cout<< " " << t2->weight << ", t: " << t->val << " " << t->weight << endl;
t->left = t1;
t->right = t2;
//合并后的树入堆
que.emplace(t->weight, t);
}
return que.top().second;
} 测试用例及结果
#include //for cout endl
#include //for vector
#include //for priority_queue
using namespace std;
struct TreeNode
{
char val;
int weight;
TreeNode* left;
TreeNode* right;
TreeNode(char c, int n) :val(c), weight(n), left(nullptr), right(nullptr) {};
TreeNode():val('*'),weight(0),left(nullptr),right(nullptr) {};
};//带权的哈夫曼编码树节点
TreeNode* huffmanCode(const vector>& file);
//file 输入文件 .first为频率 .second为字符 返回值为构建的哈夫曼编码的根节点
//这里不能将树作为参数传递,否则为传值传递不会保存构造的哈夫曼编码树
int main()
{
//哈夫曼编码树的测试用例
vector> file = { {10,'a'},{15,'e'},{12,'i'},{3,'s'},{4,'t'},{13,'b'},{1,'f'} };
cout << "HuffmanTree building progress: " << endl;
TreeNode* root = huffmanCode(file);
TreeNode* cur = root;
//层序打印各节点
queue que;
que.push(cur);
int layer = 1;
cout << "After Huffman Coding,Tree is:" << endl;
while (!que.empty())
{
int size = que.size();
cout << "Layer" << layer << ": " << endl;
layer++;
for (int i = 0; i < size; i++)
{
auto temp = que.front();
que.pop();
cout << temp->val << "," << temp->weight << " ";
if (temp->left != nullptr)
que.push(temp->left);
if (temp->right != nullptr)
que.push(temp->right);
}
cout << endl;
}
return 0;
} 为了方便打印,将图10.19中的'sp'换为字符'b','nl'换为字符'f'。结果如下,可对应上述算法更新图理解。
1.4.4 Trie前缀树C++实现
Leetcode208. Implement Trie (Prefix Tree) https://leetcode.com/problems/implement-trie-prefix-tree/submissions/
C++解答https://github.com/AnkangH/LeetCode/blob/master/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84/%E6%A0%91/208.%20Implement%20Trie%20(Prefix%20Tree).cpp
前缀树Trie与上述哈夫曼编码树不同,是一种用于检索单词和单词前缀的数据结构。假如有10000个单词,单词长度不同,如果使用哈希表检索单词,时间复杂度较低。但是如果检查前缀,那么构造哈希表所需时间复杂度太高。假设长度最长的单词长度为M,检查任意前缀所需要构造的哈希表,至少为O(M*N*26),k表示前缀的长度,26是将前缀每一位变换得到的key值。前缀树本质上是M树,如果是小写字母,那么m=26。简单Trie树中每个节点包含信息至少有:该节点的字母,一个bool型标志是否有单词以当前字母结束,以及一个包含26个子节点的链表,表示当前节点是否与之后的节点组成某个单词。根节点不表示任何信息,从根节点开始,每一层节点代表单词的第i位字母是否出现。还可通过增加一个变量用于计数,统计到当前字母的前缀出现多少次。简单Trie树应包含插入,检索单词和检索前缀等操作。
如上图所示前缀树,包含"aaaa""acc""egg"三个字符串。如果要插入新字符串"string",那么从根节点出发,依次检查string各位字母的对应节点是否为nullptr,并相应增加节点,到最后一个字母g时,标记end=true。如果要检查字符串是否在Trie树中,那么依次检查对应各位是否为nullptr,并且最后一个字母的标记end是否为true。同理,如果要检查某前缀是否在Trie树中,如检查字符串是否在Trie树中,只是不需最后一个字母的标记为true。
前缀树节点
struct TrieNode
{
char val;//当前字母
bool end;//标记单词结尾
//int count;//标记前缀计数
TrieNode* next[26];//子节点
TrieNode(char c)//初始化
{
val = c;
end = false;
count = 0;
for (int i = 0; i < 26; i++)
next[i] = nullptr;//注意一定要将子节点初始化为nullptr,否则如果不使用new声明
}//可能出现野指针的情况
};前缀树插入操作
void trieInsertWord(TrieNode* root, string word)
{
if (word.empty())
return;
TrieNode* cur = root;
int sizeWord = word.size();
for (int i=0;inext[word[i] - 'a'] != nullptr)
{
cur = cur->next[word[i] - 'a'];
if (i == sizeWord - 1)
cur->end = true;
}
else
{
cur->next[word[i] - 'a'] = new TrieNode(word[i]);
cur = cur->next[word[i] - 'a'];
if (i == sizeWord - 1)
cur->end = true;
}
}
} 前缀树查询字符串操作
bool trieCheckWord(TrieNode* root, string word)
{
if (word.empty())
return false;
int sizeWord = word.size();
TrieNode* cur = root;
bool res;
for (int i=0;inext[word[i] - 'a'] != nullptr)
{
if (cur->next[word[i] - 'a']->val != word[i])
return false;
else
{
cur = cur->next[word[i] - 'a'];
if (i == sizeWord - 1)
res = cur->end;
}
}
else
return false;
}
return res;
} 前缀树查询前缀操作
bool trieCheckPrefix(TrieNode* root, string prefix)
{
if (prefix.empty())
return false;
int sizePrefix = prefix.size();
TrieNode* cur = root;
bool res;
for (int i = 0; i < sizePrefix; i++)
{
if (cur->next[prefix[i] - 'a'] != nullptr)
{
if (cur->next[prefix[i] - 'a']->val != prefix[i])
return false;
else
{
cur = cur->next[prefix[i] - 'a'];
if (i == sizePrefix-1)
res = true;
}
}
else
return false;
}
return res;
}前缀树插入,查询字符串,查询前缀测试
#include
#include
using namespace std;
struct TrieNode
{
char val;
bool end;
int count;
TrieNode* next[26];
TrieNode(char c)
{
val = c;
end = false;
count = 0;
for (int i = 0; i < 26; i++)
next[i] = nullptr;
}
};
void trieInsertWord(TrieNode* root, string word);
bool trieCheckWord(TrieNode* root, string word);
bool trieCheckPrefix(TrieNode* root, string prefix);
int main()
{
auto root = new TrieNode('*');
string str = "string";
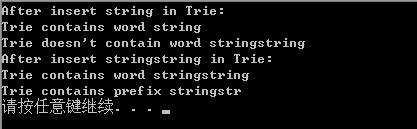
cout << "After insert " << str << " in Trie: " << endl;
trieInsertWord(root, str);
if (trieCheckWord(root, str))
cout << "Trie contains word " << str << endl;
else
cout << "Trie doesn't contain word " << str << endl;
str = "stringstring";
if (trieCheckWord(root, str))
cout << "Trie contains word " << str << endl;
else
cout << "Trie doesn't contain word " << str << endl;
trieInsertWord(root,str);
cout << "After insert " << str << " in Trie: " << endl;
if (trieCheckWord(root, str))
cout << "Trie contains word " << str << endl;
else
cout << "Trie doesn't contain word " << str << endl;
string prefix = "stringstr";
if (trieCheckPrefix(root, prefix))
cout << "Trie contains prefix " << prefix << endl;
else
cout << "Trie doesn't contain prefix " << prefix << endl;
return 0;
} 1.5装箱问题(bin packing )
给出一定属性的箱子和一定属性的物品,要求将物品放入箱子中,保证某个属性最佳,称为装箱问题。装箱问题分为联机装箱问题和脱机装箱问题,区别在于是否顺序放入物品,联机装箱问题要求当前物品放入一个箱子后才可以处理下一个物品。
1.5.1联机装箱问题
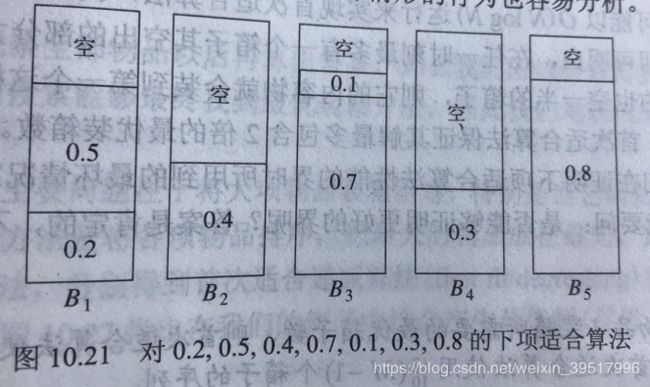
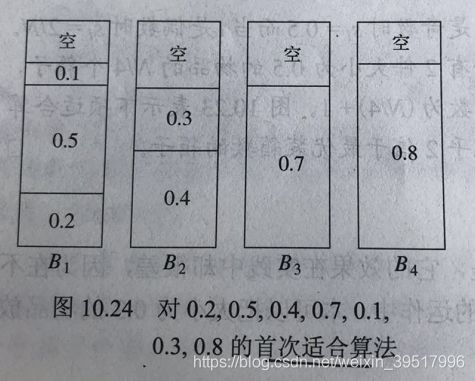
联机装箱要求将每个物品放入一个箱子后才可以处理下个箱子,因此即便之后的序列中有更合适的箱子,也不能放入,因而解不是全局最优的。解决联机装箱问题有三种简单算法:下项适合算法(next fit),首次适合算法(first fit),最佳适合算法(best fit),这三种算法都能保证对于N个物品,若最优装箱数为M,则算法求得的装箱数下界为2M。
下项适合算法(next fit)处理物品p[i]时,查看p[i-1]所在的箱子b[k]是否能装入p[i],若能,放入b[k],否则放入新箱子。因为只考虑了前一个物品所在的箱子,所以效果最差。
首次适合算法(first fit)处理物品p[i]时,查看所有的箱子b[i],放入第一个能放入p[i]的箱子b[k]。因为找到第一个合适的箱子后即放入该箱子,而后面可能有更适合的箱子,所以效果较差。
最佳适合算法(best fit)处理物品p[i]时,查看所有的箱子b[i],放入最适合的箱子b[k](如放入p[i]后,p[k]的剩余空间最小)中。
1.5.2 脱机装箱问题
脱机装箱问题使得可以遍历所有的物品获取物品的属性,从而使装箱的结果更优。解决脱机装箱问题的方法是首次适合递减算法和最佳适合递减算法,是对联机装箱问题的这两种方法,将物品大小降序排序后执行的结果,因为越大的物品在箱子已有物品的情况下越难放入。
1.6 0-1背包问题
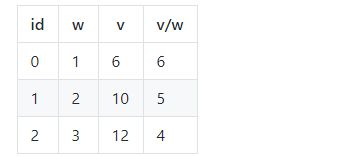
0-1背包问题是装箱问题的推广,物品有多个属性如体积,价值等,箱子通常只有一个属性即大小。0-1是指物品只有两个状态,在箱子中(选择,1)和不在箱子中(不选择,0)。0-1背包问题不能使用贪婪算法求解,考虑如下的物品,w为体积,v为价值,v/w指单位价值。如果有一个大小为5的箱子,从以下三个物品中选取任意个装入箱子,使箱子中的物品价值最大。将单位价值降序排序后,无论是首项适合递减算法还是最佳适合递减算法,都会将物品0放入箱子中,而最佳的选择是选物品1和2。如果按体积排序,因为体积与价值不相关,无法获得最优方案。同理按价值降序排序也不可,反例为增加一个体积为5,价值为13的物品。0-1背包问题的解决方法是动态规划,即找到每个阶段之间的 递归关系,而不是简单的利用贪婪思想,将每个阶段最优化而不考虑对未来的影响。见3.2 0-1背包问题。
2.分治算法
3.动态规划
动态规划问题的核心在于定义递推变量dp[i]以及找到递推公式dp[i]=?dp[j],j Leetcode139. Word Break https://leetcode.com/problems/word-break/ https://github.com/AnkangH/LeetCode/blob/master/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92/139.%20Word%20Break 题目:给定一个单词word和词典dict,判断单词可否由字典中的单词组成。 首先定义dp[i]为单词前i位是否能被字典组成,那么递推公式为dp[i]=dp[j]&& string(i-j) is in dict?,0 因此这道题有两个思路,通过dp[j]遍历和通过string(i-j)遍历。通过dp[j]遍历是指对于分割的单词前i位,对所有的j 416. Partition Equal Subset Sum https://leetcode.com/problems/partition-equal-subset-sum/ C++解答https://github.com/AnkangH/LeetCode/blob/master/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92/416.%20Partition%20Equal%20Subset%20Sum 给定一个输入正整数数组,判断是否可以将数组分为两部分,使这两部分的和相等。假设这个和为sum1,那么sum1为数组总的和sum/2。首先判断边界条件为数组的和能整除2,然后问题就转换为了在长度为N的数组中任意取出k个,使和为sum1。是0-1背包的变体,每个数字只有两个状态,在背包中和不在背包中,但是目标是使背包的总价值为sum1,而不是最小化或最大化。 确定dp[i]的定义和递推公式。考虑与3.1字符串分割的区别,对于字符串分割,因为字符串是连续的,所以只有一个变量就是前i项,值为是否能由字典组成。而对于在数组中找出任意项,和为sum,选出的项可以不连续,个数也不确定,因而有两个变量,一个是前i项,一个是数组和sum,如果只有一个的话无法递推。如只选数组和sum为变量 ,那么dp[i]的定义是,数组能否选取任意项,和为i。递推公式为dp[i]=dp[j]&&i-j in nums,存在重复利用元素的问题,如2,6这个数组,dp[2]在数组中,2在数组中,那么dp[4]为true,原因是对同一个元素2重复使用,而且也不能在使用了之后就删去,因为所有的i>2都可能利用2这个元素,而无法分辨到底是哪个利用了这个元素。 确定dp[i][j]的定义为前i项,是否可以组成和j。有三种情况,前i-1项可以组成和j,那么dp[i][j]=dp[i-1][j]=true;第二种情况,前i-1项不能组成j,dp[i-1][j]=false,但j>nums[i]又前i-1项可以组成j-nums[i](dp[i-1][j-nums[i]]==true),注意索引的对齐,因为dp[i][j],i下标从1开始,那么nums[i]应该为nums[i-1],此时dp[i][j]=true;除此之外,dp[i][j]均为fallse。遍历i,j更新动态变量dp即可。 3.1单词分割问题
C++实现 3.1.1 以后部分单词string(i-j)遍历
class Solution {
public:
bool wordBreak(string s, vector3.1.2 以动态记录表dp[i]遍历
class Solution {
public:
bool wordBreak(string s, vector3.2 0-1背包问题
class Solution {
public:
bool canPartition(vector