状态估计第二讲:线性高斯系统的状态估计问题

来源：深蓝学院《机器人学中的状态估计》

本讲的核心问题就是线性系统卡尔曼滤波的推导。

离散时间的批量估计

线性高斯模型

运动方程：$x_k=A_{k-1}{x}_{k-1}+v_k+w_k,k=1,2\dots \dots K$
观测方程：$y_k=C_k{x}_k+n_k,k=0,1,2\dots \dots K$
各个变量的意义：
系统状态：$x_k\in {\mathbb{R}}^N$
初始状态：$x_0\in {\mathbb{R}}^N\sim N(\check{x_0},\check{P_0})$
输入：$v_k\in {\mathbb{R}}^N$
状态转移矩阵：$A_{k-1}$
过程噪声：$w_k\in {\mathbb{R}}^N\sim N(0,Q_k)$
观测矩阵：$C_K$
观测噪声：$n_k\in {\mathbb{R}}^N\sim N(0,R_k)$
观测量：$y_k\in {\mathbb{R}}^N$
状态估计问题： 通过初始状态、各时刻的观测数据、输入数据，估计系统的真实状态

最大后验估计(MAP)

MAP问题：已知输入和观测，求最大概率的状态
$\hat{x}=arg\underset{x}{\max }p(x|y,v)$
用贝叶斯公式重写上述公式
$\hat{x}=arg\underset{x}{\max }\frac{p(y|x,v)\ast p(x|v)}{p(y|v)}=arg\underset{x}{\max }p(x|v)p(y|x)$
由于各个时刻观测、输入的噪声都是无关的，上面两个项可以因式分解：
$p(x|v)=p(x_0|{\check{x}}_0){\prod }_{k=1}^{K}p(x_k,|x_{k-1},v_k)$
$p(y|x)={\prod }_{k=0}^{K}p(y_k|x_k)$
对目标函数取对数可得：
$\ln (p(y|x)p(x|v))=\ln p(x_0|\check{x_0})+{\sum }_{k=1}^K\ln p(x_k|x_{k-1},v_k)+{\sum }_{k=0}^K\ln p(y_k|x_k)$
将概率化成相应的数学形式有：
$\ln p(x_0|{\check{x}}_0)=-\frac{1}{2}(x_0-{\check{x}}_0{)}^T{\check{P}}_0^{-1}(x_0-{\check{x}}_0)-\frac{1}{2}\ln ((2\pi {)}^{N}det{\check{P}}_0)$
$\ln p(x_k|x_{k-1},v_k)=-\frac{1}{2}(x_k-A_{k-1}{x}_{k-1}-v_k{)}^T{Q}_k^{-1}(x_k-A_{k-1}{x}_{k-1}-v_k)-\frac{1}{2}\ln ((2\pi {)}^{N}det{Q}_k)$
$\ln p(y_k|x_k)=-\frac{1}{2}(y_k-C_k{x}_k{)}^T{R}_k^{-1}(y_k-C_k{x}_k)-\frac{1}{2}\ln ((2\pi {)}^{M}det{R}_k)$
去掉与$x$无关的项，定义如下等式：
$J_{v,k}(x)=\{\begin{array}{l}-\frac{1}{2}(x_0-{\check{x}}_0{)}^T{\check{P}}_0^{-1}(x_0-{\check{x}}_0),k=0\\ -\frac{1}{2}(x_k-A_{k-1}{x}_{k-1}-v_k{)}^T{Q}_k^{-1}(x_k-A_{k-1}{x}_{k-1}-v_k),k=1,\dots \dots K\end{array}$
$J_{y,k}(x)=-\frac{1}{2}(y_k-C_k{x}_k{)}^T{R}_k^{-1}(y_k-C_k{x}_k),k=0,\dots \dots ，K$
于是目标函数变成最小二乘问题：
$\hat{x}=\arg \underset{x}{m}ax{J}_x,J_x={\sum }_{k=0}^K(J_{v,k}(x)+J_{y,k}(x))$
写成更紧凑的矩阵形式：

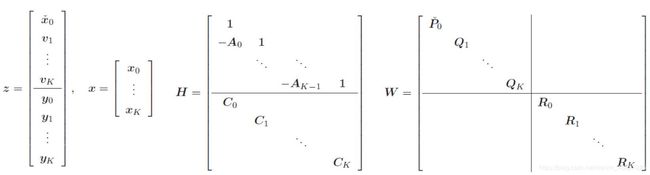
把运动和观测写在一起：
$z=Hx+W$
提升形式的目标函数：
$J(x)=\frac{1}{2}(z-Hx{)}^T{W}^{-1}(z-Hx)$
该式是个二次的，求其最小值，只令自变量最小值导数为0：
$\frac{\partial J(x)}{\partial x^T}=-H^T{W}^{-1}(z-H\hat{x})=0$
$\Rightarrow (H^T{W}^{-1}H)\hat{x}=H^T{W}^{-1}z$

贝叶斯推断

在LG(线性高斯)系统中，可以根据运动方程和观测方程显式写出状态变量分布的变化过程。
单个时刻：
$x_k=A_{k-1}{x}_{k-1}+v_k+w_k$
提升形式：
$x=A(v+w)$
$A=\left[\begin{array}{cccccc}1& & & & & \\ A_0& 1& & & & \\ A_1{A}_0& A_1& 1& & & \\ ⋮& ⋮& ⋮& & & \\ A_{K-1}\dots A_0& A_{K-2}\dots A_1& A_{K-2}\dots A_2& \dots & 1& \\ A_{K-1}\dots A_0& A_{K-1}\dots A_1& A_{K-1}\dots A_2& \dots & A_{K-1}& 1\end{array}\right]$
提升形式里，右侧只有v和w，容易求得其均值和协方差：
$\check{x}=E[x]=E[A(v+w)]=Av$
$\check{P}=E[(x-E[x])(x-E[x]{)}^T]=AQ{A}^T$
先验部分写为:$p(x|v)=N(\check{x},\check{P})=N(Av,AQ{A}^T)$
观测模型：
单次观测：$y_k=C_k{x}_k+n_k$
提升形式：$y=Cx+n,C=diag(C_0,C_1，\dots \dots C_K)$
联合分布：
$p(x,y|v)=N(\left[\begin{array}{c}\check{x}\\ C\check{x}\end{array}\right],\left[\begin{array}{cc}\check{P}& \check{P}{C}^T\\ C\check{P}& C\check{P}{C}^T+R\end{array}\right])$
由第一章的高斯推断可得：
$p(x|v,y)=N(\check{x}+\check{P}{C}^T(C\check{P}{C}^T+R{)}^{-1}(y-C\check{x}),\check{P}-\check{P}{C}^T(C\check{P}{C}^T+R{)}^{-1}C\check{P})$
带入SMW式进行化简可得：
$p(x|v,y)=N(\begin{array}{cc}({\check{P}}^{-1}+C^T{R}^{-1}C{)}^{-1}({\check{P}}^{-1}\check{x}+C^T{R}^{-1}y),& ({\check{P}}^{-1}+C^T{R}^{-1}C{)}^{-1})\\ 均值\hat{x}& 后验协方差\hat{P}\end{array}$
均值部分：$({\check{P}}^{-1}+C^T{R}^{-1}C)\hat{x}={\check{P}}^{-1}\check{x}+C^T{R}^{-1}y$
代入$\check{x}=Av$和${\check{P}}^{-1}=A^{-T}{Q}^{-1}{A}^{-1}$
得均值式：$(A^{-T}{Q}^{-1}{A}^{-1}+C^T{R}^{-1}C)\hat{x}=A^{-T}{Q}^{-1}v+C^T{R}^{-1}y$
由于A的结构，A逆具有特殊形式：
$A^{-1}=\left[\begin{array}{ccccc}1& & & & \\ -A_0& 1& & & \\ & -A_1& 1& & \\ & & -A_2& \ddots & \\ & & \ddots & 1& \\ & & & -A_{K-1}& 1\end{array}\right]$
按照均值式，定义矩阵:
$z=\left[\begin{array}{c}v\\ y\end{array}\right],H=\left[\begin{array}{c}{A}^{-1}\\ C\end{array}\right],W=\left[\begin{array}{cc}Q& \\ & R\end{array}\right]$
可得：$(H^T{W}^{-1}H)\hat{x}=H^T{W}^{-1}z$与MAP结果完全一致!
MAP结果和贝叶斯推断结果一致，说明了什么？
• MAP只关心达到最大后验概率的一个点，这个点的状态称为MAP估计。
• 而贝叶斯推断写出了p(x|y,v)的完整形式，它是一个高斯分布，其均值与MAP估计相等；同时，给出了这个估计的协方差。
• 如果我们只关心状态估计变量取值，那么MAP给出了后验分布的模（Mode），贝叶斯推断给出了均值。
• 而在LG系统中，二者是一样的，使得这两类方法给出了同样的结果。
LG系统最优估计结果唯一的条件：$rank(H^T{W}^{-1}H)=N(K+1),N(K+1)表示x的维度$。
由于协方差矩阵的对称正定性，即要求$rank(H^{T}H)=rank(H^T)=N(K+1)$
H的具体形式取决于问题有没有0时刻的先验条件。

离散时间的递归平滑算法

很多在线问题当中（比如定位），我们有上一个时刻的先验估计，希望通过这个时刻的控制和观测，计算这个时刻的状态估计。这里介绍递归解法。递归解法的基础是批量问题的解法。
批量问题的核心是用Cholesky分解法求解方程$(H^T{W}^{-1}H)\hat{x}=H^T{W}^{-1}z$
Cholesky解方程的流程：
•Cholesky分解：$H^T{W}^{-1}H=L{L}^T$
• 先解：$Ld=H^T{W}^{-1}z$ 得到d，从上往下解；
• 再解： $L^T\hat{x}=d$得到最优状态，从下往上解；
• 注意这种解法对一般线性方程也是有效的，不光是针对状态估计问题
• 这两步分别称为前向过程和后向过程（forward/backward）。
迭代法是建立在Cholesky基础上，最终得到经典的RTS Smoother：
前向：$k=1,\dots \dots ,K$
${\check{P}}_{k,f}=A_{k-1}{\hat{P}}_{k-1,f}{A}_{k-1}^T+Q_k$
${\check{x}}_{k,f}=A_{k-1}{\hat{x}}_{k-1,f}+v_k$
$K_k={\check{P}}_{k,f}{C}_k^T(C_k{\check{P}}_{k,f}{C}_k^T+R_k{)}^{-1}$
${\hat{P}}_{k,f}=(1-K_k{C}_k){\check{P}}_{k,f}$
${\hat{x}}_{k,f}={\check{x}}_{k,f}+K_k(y_k-C_k{\check{x}}_{k,f})$
后向：$k=K,\dots \dots ，1$
${\hat{x}}_{k-1}={\hat{x}}_{k-1,f}+{\hat{P}}_{k-1,f}{A}_{k-1}^T{\check{P}}_{k,f}^{-1}({\hat{x}}_k-{\check{x}}_{k,f})$

离散时间的滤波算法

• RTS Smoother是无法在线运行的（非因果的Not causal）
• 它的后向迭代过程使用下个时刻的信息更新之前的估计
• 初始值中需要知道x(K)的后验

利用MAP和贝叶斯推断均可推导出卡尔曼滤波，在此只给出卡尔曼滤波最终形式：

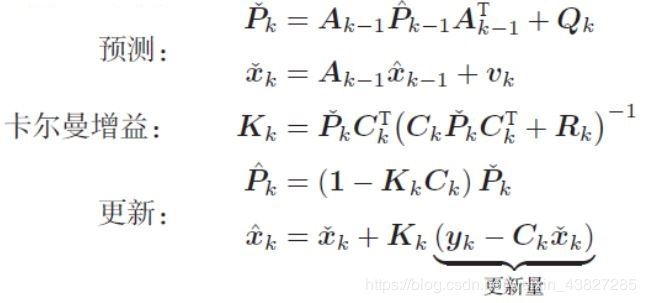
关于卡尔曼滤波器的结论
• 卡尔曼滤波器给出了LG系统下最优线性无偏估计（Best Linear Unbiased Estimate, BLUE）
• 需要有初始状态
• 卡尔曼滤波器即RTS Smoother的前向部分
• 在非线性场合下，我们会使用扩展卡尔曼滤波器（EKF），但此时MAP、贝叶斯推断、EKF给出的结果均会不一样