2020上海高校程序设计竞赛暨第18届上海大学程序设计联赛夏季赛（同步赛）解题报告ABCEG
题目链接：https://ac.nowcoder.com/acm/contest/6871
A-同源
题意
- Compute 对于某些特殊的数字有着独特的爱好。
- 例如，有三个正整数 a, b, c 和某一个目标值 k，如果 gcd(a,b)=gcd(b,c)=gcd(a,c)=k，并且 a,b,c≠k ，那么他认为这三个数是一组好数。 其中gcd(x,y)表示整数 x 和 y 的最大公约数。
- 当然这不够刺激。现在 Compute 想要知道，如果已知三个数的和 n 和目标值 k，是否存在一组 a, b, c 可以让它们是一组好数。有的话输出任意一组，否则输出-1 -1 -1
思路
- 只需要找出三个互质的数，他们的和为 n/k 即可
- 当n不是k的倍数时，三个数的最大公约数肯定不是k，输出-1 -1 -1
- 否则都能找到满足条件的解，前两个数暴力枚举100，然后判断三个数是否互质即可
AC代码
#include
#define LL long long
#define sc(a) scanf("%d", &a)
#define sc2(a, b) scanf("%d%d", &a, &b)
#define sc3(a, b, c) scanf("%d%d%d", &a, &b, &c)
#define scl(a) scanf("%lld", &a)
#define scl2(a, b) scanf("%lld%lld", &a, &b)
#define ss(a) scanf("%s", a)
#define mem(a, b) memset(a, b, sizeof(a))
#define PII pair
using namespace std;
const int maxn = 5e5 + 5;
const int mod = 1e9+7;
int main(){
int t;sc(t);
while(t--){
LL n,k;
scl2(n,k);
if(n%k){
cout<<"-1 -1 -1\n";
continue;
}n/=k;
int f=0;
for(LL i=2;i<=100;i++){
for(LL j=2;j<=100;j++){
LL kk=n-i-j;
if(kk>1&&__gcd(i,j)==1&&__gcd(i,kk)==1&&__gcd(j,kk)==1){
cout< B-分子
题意
- 求有机分子式量。一个 C 原子的式量为 13 ，一个 H 原子的式量为 1 ，一个 O 原子的式量为 17 。一个有机分子的式量恰为各个原子的式量的总和。
- 原子后面带有数字表示原子的个数，括号后面带有数字表示整体的个数
- 括号不嵌套括号
思路
- 字符串模拟。
- 带有括号的分开模拟，一块一块计算，这里写了个cal函数，不带括号的处理方式一样的
- 注意的是后面表示原子的个数可能会爆int，也要用long long存
AC代码
#include
#define LL long long
#define sc(a) scanf("%d", &a)
#define sc2(a, b) scanf("%d%d", &a, &b)
#define sc3(a, b, c) scanf("%d%d%d", &a, &b, &c)
#define scl(a) scanf("%lld", &a)
#define scl2(a, b) scanf("%lld%lld", &a, &b)
#define ss(a) scanf("%s", a)
#define mem(a, b) memset(a, b, sizeof(a))
#define PII pair
using namespace std;
const int maxn = 5e5 + 5;
const int mod = 1e9 + 7;
map mp;//存原子式量
LL cal(string a)
{
LL ans = 0;
for (int i = 0; i < a.size(); i++)
{
if (i + 1 < a.size() && isdigit(a[i + 1]))//判断后面是不是数字
{
int p = i + 1;
LL s = 0;//数字可能很大，开long long
while (p < a.size() && isdigit(a[p]))
{
s = s * 10 + a[p] - '0';//拿s存数字
p++;
}
ans += mp[a[i]] * s;
i = p - 1;//到下一个字符前一个位置，因为后面要++
}
else
ans += mp[a[i]];
}
return ans;
}
int main()
{
mp['C'] = 13;
mp['H'] = 1;
mp['O'] = 17;
LL ans = 0;
string a;
cin >> a;
for (int i = 0; i < a.size(); i++)
{
if (a[i] == '(')
{
int p = i;
LL s = 0, tmp = 0;
while (a[p] != ')')
p++;
tmp = cal(a.substr(i + 1, p - i - 1));//括号内分子式量
p++;
if (isdigit(a[p]))//判断括号后面是不是数字
{
while (p < a.size() && isdigit(a[p]))
{
s = s * 10 + a[p] - '0';//存分子个数
p++;
}
}
else
s = 1;
ans += tmp * s;
i = p - 1;
}
else
{
//不是括号的话，处理方式一样的
if (i + 1 < a.size() && isdigit(a[i + 1]))
{
int p = i + 1;
LL s = 0;
while (p < a.size() && isdigit(a[p]))
{
s = s * 10 + a[p] - '0';
p++;
}
ans += mp[a[i]] * s;
i = p - 1;
}
else
ans += mp[a[i]];
}
// cout << "i:" << i << endl;
// cout << "ans:" << ans << endl;
}
cout << ans << endl;
system("pause");
return 0;
} C-爵士
题意
- 给你n行字符串，如果一个字符串中包含2，那么他就很二次元。
- 问该组样例的二次元浓度
思路
- 水题。
- 因为每行中会有括号存在，所以要用到gets(str)；或者getline(cin,s)；输入 。前者是char类型，后者是string类型
- 由于上面两种方式会吸收所有字符，到回车为止，为了防止第一行吸收输入n后面的回车，我们就要在输入n之后加上一行getchar();来吸收那个回车。
AC代码
#include
#define LL long long
#define sc(a) scanf("%d", &a)
#define sc2(a, b) scanf("%d%d", &a, &b)
#define sc3(a, b, c) scanf("%d%d%d", &a, &b, &c)
#define scl(a) scanf("%lld", &a)
#define scl2(a, b) scanf("%lld%lld", &a, &b)
#define ss(a) scanf("%s", a)
#define mem(a, b) memset(a, b, sizeof(a))
#define PII pair
using namespace std;
const int maxn = 5e5 + 5;
const int mod = 1e9+7;
int main(){
int t;cin>>t;
while(t--){
int n,cnt=0;cin>>n;
//cout<<"n:"< E-内存
题意
- 给定32位二进制代码，后p位是页码，前32-p位是虚拟页码，为了简洁，题目给了8位十六进制的数
- 给一张表是虚拟页码对应的物理页码，如果存在的话，那么就把虚拟页码转换成物理页码，并输出十六进制的值，否则输出“interrupt!”
思路
- 大模拟，细心一点就能过。
AC代码
#include
#define LL long long
#define sc(a) scanf("%d", &a)
#define sc2(a, b) scanf("%d%d", &a, &b)
#define sc3(a, b, c) scanf("%d%d%d", &a, &b, &c)
#define scl(a) scanf("%lld", &a)
#define scl2(a, b) scanf("%lld%lld", &a, &b)
#define ss(a) scanf("%s", a)
#define mem(a, b) memset(a, b, sizeof(a))
#define PII pair
using namespace std;
const int maxn = 5e5 + 5;
const int mod = 1e9+7;
mapmp;
int main(){
int n,m,p;
sc3(n,m,p);
for(int i=0;i<(1<<(m-p));i++){//一共有(1<<(m-p))页，也就是2^(m-p)
LL x;scl(x);
mp[x]=i+1;//由于存在i=0，会对后面的判断产生影响，这边先给他算i+1，后面取出-1就好了
}
int q;sc(q);
while(q--){
char a[105];ss(a);
vectorb;
for(int i=0;is;
for(int j=0;j<4;j++){//自己会补零
s.push(tmp%2);
tmp/=2;
}
//由于上面存的是二进制余数，这边就要倒着存，所以用了栈
while(s.size()){
b.push_back(s.top());
s.pop();
}
}
//计算虚拟地址页号
LL tt=0,bas=1;
for(int i=32-p-1;i>=0;i--){
if(b[i])tt+=bas;
bas<<=1;
}
if(!mp[tt]){
cout<<"interrupt!"<=0;i--){//物理页号转二进制
int x=tmp%2;
b[i]=x;
tmp/=2;
}
for(int i=0;i<32;i+=4){//二进制转十六进制并输出
tmp=0;
for(int j=i;j G-选择
题意
- 有n个数，取出
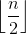（向下取整）个数，相邻的位置不可取 - 有一个条件是他一定会取x位置的数
- 问取出的数最大和是多少
思路
- dp 。
- dp[i]为1到i位最大和,sum[i]为1到i的前几位奇数的前缀和
- 状态转移方程：
![dp[i]=\left\{\begin{matrix} max(dp[i-1],dp[i-2]+a[i]) & i(odd)\\ max(dp[i-2]+a[i],sum[i-1]) & i(even) \end{matrix}\right.](http://img.e-com-net.com/image/info8/dbbe10bc3da442ebacc050421e72b4b3.gif)
- 奇数位置的时候，dp[i-1]表示当前位不选，dp[i-2]+a[i]表示当前位选，但是由于相邻位不选，那么加上dp[i-2]的状态，两种都能保证选满n/2个数
- 偶数的位置，由于要保证选满n/2个数，所以sum[i-1]表示当前为不选，前奇数位累加，个数一定等于n/2。dp[i-2]+a[i]表示当前位选，由于相邻位不选，加上dp[i-2]的状态
- 由于x位置必选，那么可以事先给他加上很大的数，比如1e16，让转移的时候必定加上这个位置，然后输出的时候-1e16就可
AC代码
#include
#define LL long long
#define sc(a) scanf("%d", &a)
#define sc2(a, b) scanf("%d%d", &a, &b)
#define sc3(a, b, c) scanf("%d%d%d", &a, &b, &c)
#define scl(a) scanf("%lld", &a)
#define scl2(a, b) scanf("%lld%lld", &a, &b)
#define ss(a) scanf("%s", a)
#define mem(a, b) memset(a, b, sizeof(a))
#define PII pair
using namespace std;
const int maxn = 2e5 + 5;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;
LL a[maxn], dp[maxn], sum[maxn], p = 1e16;
int main()
{
int n, x;
sc2(n, x);
for (int i = 1; i <= n; i++)
{
scl(a[i]);
}
a[x] += p;
sum[1] = a[1];
for (int i = 3; i <= n; i += 2)
{
sum[i] = sum[i - 2] + a[i];//前奇数位的前缀和
}
for (int i = 2; i <= n; i++)
{
if (i & 1) //奇数位置的时候，dp[i-1]表示当前位不选，dp[i-2]+a[i]表示当前位选，但是由于相邻位不选，那么加上dp[i-2]的状态
dp[i] = max(dp[i - 1], dp[i - 2] + a[i]);
else //偶数的位置，由于要保证选满n/2个数，所以sum[i-1]表示当前为不选，前奇数位累加，个数一定等于n/2。dp[i-2]+a[i]表示当前位选，由于相邻位不选，加上dp[i-2]的状态
dp[i] = max(sum[i - 1], dp[i - 2] + a[i]);
}
cout << dp[n] - p << endl;
system("pause");
return 0;
}