比PCA更好用的监督排序—LDA分析、作图及添加置信-ggord

线性判别分析LDA

线性判别分析，英文Linear Discriminant Analysis, 以下简称LDA。LDA在模式识别领域（比如人脸识别，舰艇识别等图形图像识别领域）中有非常广泛的应用，在生物学大数据研究中同样也有广泛应用，比如前几个月的Sicence封面文章哈扎人菌群研究就使了此方法，因此我们有必要了解下它的算法原理[1]。

LDA的思想

LDA是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”。什么意思呢？ 我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。

　可能还是有点抽象，我们先看看最简单的情况。假设我们有两类数据 分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

图1. LDA排序原理模式

上图提供了两种投影方式，哪一种能更好的满足我们的标准呢？从直观上可以看出，右图要比左图的投影效果好，因为右图的黑色数据和蓝色数据各个较为集中，且类别之间的距离明显。左图则在边界处数据混杂。以上就是LDA的主要思想了，当然在实际应用中，我们的数据是多个类别的，我们的原始数据一般也是超过二维的，投影后的也一般不是直线，而是一个低维的超平面[1]。

更多算法和原理解析，可阅读参考文献[1]。

LDA排序和ggord添加椭圆置信区间

# Installation
devtools::install_github('fawda123/ggord')

# 加载lda包
library(MASS)

# 查看测试数据
head(iris)

# 按物种分组LDA排序
ord <- lda(Species ~ ., iris, prior = rep(1, 3)/3)

# 展示LDA分析
library(ggord)
p <- ggord(ord, iris$Species)
p

图2. 以鸢尾花尺寸属性按品种分组上色，并添加半透明色0.95置信背景椭圆。箭头为花尺寸各属性与LD1/2轴的相关和贡献[4]。

# 计算置信椭圆函数

get_lda_ell <- function(ord_in, grp_in, ellipse_pro = 0.97){
  ## adapted from https://github.com/fawda123/ggord/blob/master/R/ggord.R
  require(plyr)
  axes = c('LD1', 'LD2')
  obs <- data.frame(predict(ord_in)$x[, axes])
  obs$Groups <- grp_in
  names(obs)[1:2] <- c('one', 'two')
  theta <- c(seq(-pi, pi, length = 50), seq(pi, -pi, length = 50))
  circle <- cbind(cos(theta), sin(theta))
  ell <- ddply(obs, 'Groups', function(x) {
    if(nrow(x) <= 2) {
      return(NULL)
    }
    sigma <- var(cbind(x$one, x$two))
    mu <- c(mean(x$one), mean(x$two))
    ed <- sqrt(qchisq(ellipse_pro, df = 2))
    data.frame(sweep(circle %*% chol(sigma) * ed, 2, mu, FUN = '+'))
  })
  names(ell)[2:3] <- c('one', 'two')
  ell <- ddply(ell, .(Groups), function(x) x[chull(x$one, x$two), ])
  ell
}

# 计算置信椭圆，并添加至原图
anotherEll <- get_lda_ell(ord, iris$Species, 0.97)
## Loading required package: plyr
p + geom_polygon(data = anotherEll, 
                 aes_string(color = 'Groups', group = 'Groups'),
                 lty=2, fill = NA)

图3. 添加0.97置信区间的虚线椭圆

以菌群测试数据实战

# 读入实验设计
design = read.table("design.txt", header=T, row.names= 1, sep="\t") 
# 读取OTU表
otu_table = read.delim("otu_table.txt", row.names= 1,  header=T, sep="\t")
# 转换原始数据为百分比
norm = t(t(otu_table)/colSums(otu_table,na=T)) * 100 # normalization to total 100
# 按mad值排序取前6波动最大的OTUs
mad.5 = head(norm[order(apply(norm,1,mad), decreasing=T),],n=6)
row.names(mad.5)=c("Streptophyta","Rubrivivax","Methylibium","Streptosporangiaceae","Streptomyces","Niastella")
data=as.data.frame(t(mad.5))
# 添加分组信息
data$group=design[row.names(data),]$genotype

# 按实验基因组分组排序
ord <- lda(group ~ ., data)

# 使用ggbiplot展示lda(可选)
library(ggbiplot)
ggbiplot(ord, obs.scale = 1, var.scale = 1,
         groups = data$group, ellipse = TRUE,var.axes = F)

# 展示LDA分析
library(ggord)
p <- ggord(ord, data$group, ellipse_pro = 0.68)
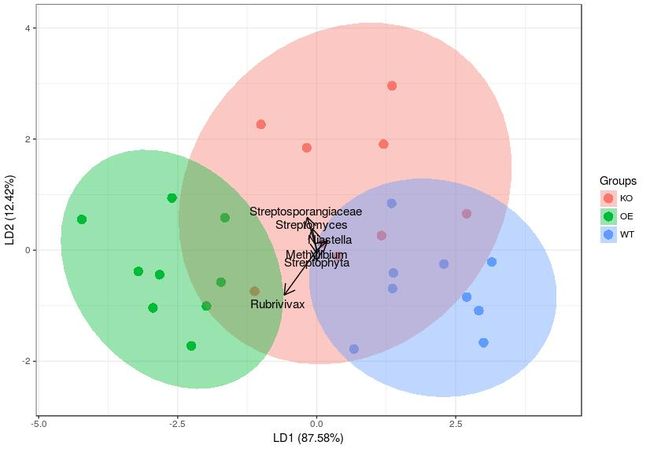
p

图4. LDA分析三组6个高度差异菌的分组+背景置信区间

anotherEll <- get_lda_ell(ord, data$group, 0.97)
p + geom_polygon(data = anotherEll, 
                 aes_string(color = 'Groups', group = 'Groups'),
                 lty=2, fill = NA)

图4. LDA分析三组6个高度差异菌的分组+背景置信区间。按68%和97%天加置信区间背景色和虚线椭圆

LDA与PCA比较

LDA用于降维，和PCA有很多相同，也有很多不同的地方，因此值得好好的比较一下两者的降维异同点。

首先我们看看相同点：

1）两者均可以对数据进行降维。

2）两者在降维时均使用了矩阵特征分解的思想。

3）两者都假设数据符合高斯分布。

我们接着看看不同点：

1）LDA是有监督的降维方法，而PCA是无监督的降维方法

2）LDA降维最多降到类别数k-1的维数，而PCA没有这个限制。

3）LDA除了可以用于降维，还可以用于分类。

4）LDA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。

这点可以从下图形象的看出，在某些数据分布下LDA比PCA降维较优。

LDA算法小结

LDA算法既可以用来降维，又可以用来分类，但是目前来说，主要还是用于降维。在我们进行实验数据组间差异分析时，LDA是一个有力的工具。下面总结下LDA算法的优缺点。

LDA算法的主要优点有：

1）在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识。

2）LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。

LDA算法的主要缺点有：

1）LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。

2）LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。

3）LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。

4）LDA可能过度拟合数据。[1]

Reference

1. 线性判别分析LDA原理总结 - 刘建平Pinard - 博客园 https://www.cnblogs.com/pinard/p/6244265.html
2. 本文方法主要参考Chenhao的博客 http://lchblogs.netlify.com/post/2017-12-22-r-addconfellipselda/
3. 《扩增子分析教程-3统计绘图-冲击高分文章》http://mp.weixin.qq.com/s/6tNePiaDsPPzEBZjiCXIRg
4. ggbiplot-最好看的PCA作图：样品PCA散点+分组椭圆+变量贡献和相关
5. ggord主页 https://github.com/fawda123/ggord

猜你喜欢

• 一文读懂：1微生物组 2进化树 3预测群落功能
• 热文：1图表规范 2DNA提取 3 实验vs分析
• 必备技能：1提问 2搜索 3Endnote
• 文献阅读 1热心肠 2SemanticScholar 3geenmedical
• 扩增子分析：1图表解读 2分析流程 3统计绘图 4群落功能 5进化树
• 科研团队经验：1云笔记 2云协作 3公众号
• 系列教程：1Biostar 2微生物组 3宏基因组
• 生物科普 1肠道细菌 2生命大跃进 3细胞的暗战 4人体奥秘

写在后面

为鼓励读者交流、快速解决科研困难，我们建立了“宏基因组”专业讨论群，目前己有国内外100+ PI，900+ 一线科研人员加入。参与讨论，获得专业解答，欢迎分享此文至朋友圈，并扫码加主编好友带你入群，务必备注“姓名-单位-研究方向-职称/年级”。技术问题寻求帮助，首先阅读《如何优雅的提问》学习解决问题思路，仍末解决群内讨论，问题不私聊，帮助同行。

学习扩增子、宏基因组科研思路和分析实战，关注“宏基因组”

点击阅读原文，跳转最新文章目录阅读
https://mp.weixin.qq.com/s/5jQspEvH5_4Xmart22gjMA