数据结构(Python实现)------前缀树
数据结构(Python实现)------ 前缀树
- 数据结构(Python实现)------前缀树
- 前缀树简介
- 基本概念
- 什么是前缀树?
- 如何表示一个前缀树?
- 方法一 数组
- 方法二 Map
- 基本操作
- 基本概念
- Insertion in Trie
- Search in Trie
- 搜索前缀
- 搜索单词
- Python实现
- 实现 Trie (前缀树)
- 解法1#:用dict模拟字典树
- 解法2#:通过创建树节点形式实现
- 实际应用
- Python实现
- Map Sum Pairs
- 单词替换
- 添加与搜索单词 - 数据结构设计
- 数组中两个数的最大异或值
数据结构(Python实现)------前缀树
前缀树简介
基本概念
什么是前缀树?
前缀树是N叉树的一种特殊形式。通常来说,一个前缀树是用来存储字符串的。前缀树的每一个节点代表一个字符串(前缀)。每一个节点会有多个子节点,通往不同子节点的路径上有着不同的字符。子节点代表的字符串是由节点本身的原始字符串,以及通往该子节点路径上所有的字符组成的。
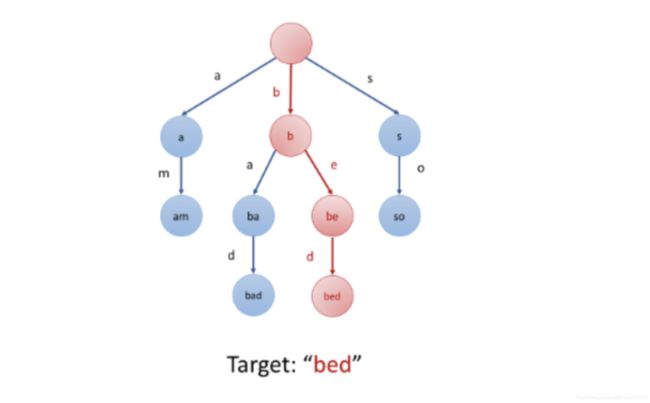
下面是前缀树的一个例子:

在上图示例中,我们在节点中标记的值是该节点对应表示的字符串。例如,我们从根节点开始,选择第二条路径 ‘b’,然后选择它的第一个子节点 ‘a’,接下来继续选择子节点 ‘d’,我们最终会到达叶节点 “bad”。节点的值是由从根节点开始,与其经过的路径中的字符按顺序形成的。
值得注意的是,根节点表示空字符串。
前缀树的一个重要的特性是,节点所有的后代都与该节点相关的字符串有着共同的前缀。这就是前缀树名称的由来。
我们再来看这个例子。例如,以节点 “b” 为根的子树中的节点表示的字符串,都具有共同的前缀 “b”。反之亦然,具有公共前缀 “b” 的字符串,全部位于以 “b” 为根的子树中,并且具有不同前缀的字符串来自不同的分支。
前缀树有着广泛的应用,例如自动补全,拼写检查等等。我们将在后面的章节中介绍实际应用场景。
如何表示一个前缀树?
方法一 数组
第一种方法是用数组存储子节点。
例如,如果我们只存储含有字母 a 到 z 的字符串,我们可以在每个节点中声明一个大小为26的数组来存储其子节点。对于特定字符 c,我们可以使用 c - ‘a’ 作为索引来查找数组中相应的子节点。
访问子节点十分快捷。访问一个特定的子节点比较容易,因为在大多数情况下,我们很容易将一个字符转换为索引。但并非所有的子节点都需要这样的操作,所以这可能会导致空间的浪费。
方法二 Map
第二种方法是使用 Hashmap 来存储子节点。
我们可以在每个节点中声明一个Hashmap。Hashmap的键是字符,值是相对应的子节点。
通过相应的字符来访问特定的子节点更为容易。但它可能比使用数组稍慢一些。但是,由于我们只存储我们需要的子节点,因此节省了空间。这个方法也更加灵活,因为我们不受到固定长度和固定范围的限制。
基本操作
基本概念
Insertion in Trie
我们已经在另一张卡片中讨论了 (如何在二叉搜索树中实现插入操作)。
提问:
你还记得如何在二叉搜索树中插入一个新的节点吗?
当我们在二叉搜索树中插入目标值时,在每个节点中,我们都需要根据 节点值 和 目标值 之间的关系,来确定目标值需要去往哪个子节点。同样地,当我们向前缀树中插入一个目标值时,我们也需要根据插入的 目标值 来决定我们的路径。
更具体地说,如果我们在前缀树中插入一个字符串 S,我们要从根节点开始。 我们将根据 S[0](S中的第一个字符),选择一个子节点或添加一个新的子节点。然后到达第二个节点,并根据 S[1] 做出选择。 再到第三个节点,以此类推。 最后,我们依次遍历 S 中的所有字符并到达末尾。 末端节点将是表示字符串 S 的节点。
下面是一个例子:
1. Initialize: cur = root
2. for each char c in target string S:
3. if cur does not have a child c:
4. cur.children[c] = new Trie node
5. cur = cur.children[c]
6. cur is the node which represents the string S
通常情况情况下,你需要自己构建前缀树。构建前缀树实际上就是多次调用插入函数。但请记住在插入字符串之前要 初始化根节点 。
Search in Trie
搜索前缀
正如我们在前缀树的简介中提到的,所有节点的后代都与该节点相对应字符串的有着共同前缀。因此,很容易搜索以特定前缀开头的任何单词。
同样地,我们可以根据给定的前缀沿着树形结构搜索下去。一旦我们找不到我们想要的子节点,搜索就以失败终止。否则,搜索成功。为了更具体地解释搜索的过程,我们提供了下列示例:


我们来用伪代码总结一下以上策略:
1. Initialize: cur = root
2. for each char c in target string S:
3. if cur does not have a child c:
4. search fails
5. cur = cur.children[c]
6. search successes
搜索单词
你可能还想知道如何搜索特定的单词,而不是前缀。我们可以将这个词作为前缀,并同样按照上述同样的方法进行搜索。
如果搜索失败,那么意味着没有单词以目标单词开头,那么目标单词绝对不会存在于前缀树中。
如果搜索成功,我们需要检查目标单词是否是前缀树中单词的前缀,或者它本身就是一个单词。为了进一步解决这个问题,你可能需要稍对节点的结构做出修改。
提示:往每个节点中加入布尔值可能会有效地帮助你解决这个问题。
Python实现
实现 Trie (前缀树)
思路:
一个Trie是通过不断insert新的字符串不断变大的。那么我们关注insert操作如何实现,便知道Trie的构造。以上面的例子为例,在构造完一个根节点后,我们要插入“apple”这个单词。我们要循着“a->p->p->l->e这个路径去逐个确认每一个前缀是否已经存在,如果不存在,就建立出这个前缀的最后一个根节点,如果存在,就继续确认下一个字母”。
解法1#:用dict模拟字典树
class Trie(object):
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = {}
def insert(self, word):
"""
Inserts a word into the trie.
:type word: str
:rtype: None
"""
node = self.root
for char in word:
node = node.setdefault(char,{})
node["end"] = True
def search(self, word):
"""
Returns if the word is in the trie.
:type word: str
:rtype: bool
"""
node = self.root
for char in word:
if char not in node:
return False
node = node[char]
return "end" in node
def startsWith(self, prefix):
"""
Returns if there is any word in the trie that starts with the given prefix.
:type prefix: str
:rtype: bool
"""
node = self.root
for char in prefix:
if char not in node:
return False
node = node[char]
return True
# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)
解法2#:通过创建树节点形式实现
class TrieNode(object):
# Initialize your data structure here.
def __init__(self):
self.children = collections.defaultdict(TrieNode)
self.is_word = False
class Trie(object):
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = TrieNode()
def insert(self, word):
"""
Inserts a word into the trie.
:type word: str
:rtype: void
"""
node = self.root
for chars in word:
child = node.data.get(chars)
if not child :
node.data[chars] = TrieNode()
node = node.data[chars]
node.is_word = True
def search(self, word):
"""
Returns if the word is in the trie.
:type word: str
:rtype: bool
"""
node = self.root
for chars in word:
node = node.data.get(chars)
if not node:
return False
# 判断单词是否是完整的存在在trie树中
return node.is_word
def startsWith(self, prefix):
"""
Returns if there is any word in the trie that starts with the given prefix.
:type prefix: str
:rtype: bool
"""
node = self.root
for chars in prefix:
node = node.data.get(chars)
if not node:
return False
return True
# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)
实际应用
Python实现
Map Sum Pairs
实现一个 MapSum 类里的两个方法,insert 和 sum。
对于方法 insert,你将得到一对(字符串,整数)的键值对。字符串表示键,整数表示值。如果键已经存在,那么原来的键值对将被替代成新的键值对。
对于方法 sum,你将得到一个表示前缀的字符串,你需要返回所有以该前缀开头的键的值的总和。
示例 1:
输入: insert("apple", 3), 输出: Null
输入: sum("ap"), 输出: 3
输入: insert("app", 2), 输出: Null
输入: sum("ap"), 输出: 5
import collections
class Node(object):
def __init__(self, count = 0):
self.children = collections.defaultdict(Node)
self.count = count
class MapSum(object):
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = Node()
self.keys = {}
def insert(self, key, val):
"""
:type key: str
:type val: int
:rtype: void
"""
curr = self.root
delta = val - self.keys.get(key, 0)
# 更新保存键值对的keys
self.keys[key] = val
curr = self.root
# 更新节点的count
curr.count += delta
for char in key:
curr = curr.children[char]
curr.count += delta
def sum(self, prefix):
"""
:type prefix: str
:rtype: int
"""
curr = self.root
for char in prefix:
if char not in curr.children:
return 0
curr = curr.children[char]
return curr.count
# Your MapSum object will be instantiated and called as such:
# obj = MapSum()
# obj.insert(key,val)
# param_2 = obj.sum(prefix)
单词替换
在英语中,我们有一个叫做 词根(root)的概念,它可以跟着其他一些词组成另一个较长的单词——我们称这个词为 继承词(successor)。例如,词根an,跟随着单词 other(其他),可以形成新的单词 another(另一个)。
现在,给定一个由许多词根组成的词典和一个句子。你需要将句子中的所有继承词用词根替换掉。如果继承词有许多可以形成它的词根,则用最短的词根替换它。
你需要输出替换之后的句子。
示例 1:
输入: dict(词典) = ["cat", "bat", "rat"]
sentence(句子) = "the cattle was rattled by the battery"
输出: "the cat was rat by the bat"
注:
输入只包含小写字母。
1 <= 字典单词数 <=1000
1 <= 句中词语数 <= 1000
1 <= 词根长度 <= 100
1 <= 句中词语长度 <= 1000
暴力法:
思路:
把sentence里的每个单词的每个子单词都在转成set的dict里查找。
class Solution(object):
def replaceWords(self, dict, sentence):
"""
:type dict: List[str]
:type sentence: str
:rtype: str
"""
dict = set(dict)
s = sentence.split(" ")
for i, word in enumerate(s):
for j in range(len(word)):
if word[:j + 1] in dict:
s[i] = word[:j + 1]
break
return " ".join(s)
前缀树法:
class TrieNode:
def __init__(self,x):
self.val = x
self.children = [None for _ in range(26)]
self.isEnd = False
class Solution(object):
def insertStr(self,str,root):
if str == None or str == "":
return
for ch in list(str):
pos = ord(ch) - ord('a')
if root.children[pos] == None:
root.children[pos] = TrieNode(ch)
else:
pass
root = root.children[pos]
root.isEnd = True
def replaceWords(self, dict, sentence):
"""
:type dict: List[str]
:type sentence: str
:rtype: str
"""
root = TrieNode(None)
for word in dict:
self.insertStr(word,root)
sentence = sentence.split(" ")
for i in range(len(sentence)):
res = ""
node = root
for j in range(len(sentence[i])):
pos = ord(sentence[i][j]) - ord('a')
if node.children[pos] != None:
res += node.children[pos].val
node = node.children[pos]
else:
break
if node.isEnd == True:
sentence[i] = res
break
return " ".join(sentence)
添加与搜索单词 - 数据结构设计
设计一个支持以下两种操作的数据结构:
void addWord(word)
bool search(word)
search(word) 可以搜索文字或正则表达式字符串,字符串只包含字母 . 或 a-z 。 . 可以表示任何一个字母。
示例:
addWord("bad")
addWord("dad")
addWord("mad")
search("pad") -> false
search("bad") -> true
search(".ad") -> true
search("b..") -> true
说明:
你可以假设所有单词都是由小写字母 a-z 组成的。
class WordDictionary(object):
def __init__(self):
"""
Initialize your data structure here.
"""
self.isword = '#'
self.root = {}
def addWord(self, word):
"""
Adds a word into the data structure.
:type word: str
:rtype: None
"""
node = self.root
for i in word:
node = node.setdefault(i,{})
node['#'] = '#'
def ennn(self, node, word):
if not word:
if '#' in node:
return True
else:
return False
i = word[0]
if i == '.':
for j in range(26):
x = chr(j + 97)
if x in node:
if self.ennn(node[x], word[1:]):
return True
return False # 这里别忘了,有个returnFalse
else:
node = node.get(i)
if not node:
return False
else:
return self.ennn(node, word[1:])
def search(self, word):
"""
Returns if the word is in the data structure. A word could contain the dot character '.' to represent any one letter.
:type word: str
:rtype: bool
"""
node = self.root
return self.ennn(node,word)
# Your WordDictionary object will be instantiated and called as such:
# obj = WordDictionary()
# obj.addWord(word)
# param_2 = obj.search(word)
数组中两个数的最大异或值
给定一个非空数组,数组中元素为 a0, a1, a2, … , an-1,其中 0 ≤ ai < 231 。
找到 ai 和aj 最大的异或 (XOR) 运算结果,其中0 ≤ i, j < n 。
你能在O(n)的时间解决这个问题吗?
示例:
输入: [3, 10, 5, 25, 2, 8]
输出: 28
解释: 最大的结果是 5 ^ 25 = 28.