JZOJ 5602 Cti

传送门

考场上的思路

  应该很接近正解吧……只不过最后有点绝妙的地方没有想出来，就爆零垫底了……

  对每个炮塔的射击范围内的每个位置都建一个点，如果有重合，那就建两个点。假设对于某个炮塔的射击范围对应的点是 a1∼ak a 1 ∼ a k ，下标越小的离炮塔越近，那么这样连边（对所有炮塔均是如此）：

S∼a1∼a2∼⋯∼ak∼T S ∼ a 1 ∼ a 2 ∼ ⋯ ∼ a k ∼ T

  其中 S S 代表源点， T T 代表汇点。（忘了说，是建成网络流的图）

  考虑建立割的模型。由于要求消灭的敌人最多（题目里好像没有说……不过题意就是这个意思），所以我们先把炮塔看作激光炮，能够消灭射击范围内的所有人（而不是一个位置的人），得到一个总和 sum s u m ，那么割边的边权就是总和减去实际能够消灭的敌人数量。

  如果你没有我这样的思路，可能很难理解，拿样例来说：

3 2
0 9
-4 3
0 -1

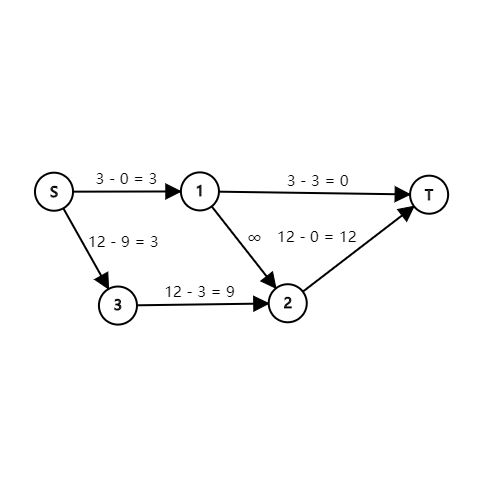
  上图中，上面的路径代表 −4 − 4 对应的攻击范围，下面的路径代表 −1 − 1 的攻击范围。

  割去源点到某个点的边，相当于不发射；割去其它边，相当于发射到某个位置。最后用总和（上例中总和为 3+12=15 3 + 12 = 15 ）去减最小割就是答案。

  然而题目有约束条件，对于上例，这个约束条件是结点 1 1 和 结点 2 2 不能同时在 S S 集合中。虽然说结点 1 1 和结点 3 3 也不能同时在 S S 集合中，但是只要满足了 1 1 和 2 2 不在 S S 集合中， 1 1 和 3 3 自然也就不在 S S 集合中了。所以我们现在的问题转化为了有“两个点不在 S S 集合中”这一约束的最小割问题。

  事实上，我会两个点在某一集合、两个点在相同集合、不允许一个点在 S S （ T T ） 集合，一个点在 T T （ S S ） 集合这三种模型。两个点不在同一指定集合的建模方法可能根本不存在……然后我就爆零了。

正解

  沿着我之前的思路走，正解其实很简单。之前我们规定 S S 集合代表选， T T 集合代表不选（这个很难说准确，感性理解下），要解决的问题就是两个点不在 S S 集合中的约束。我们直接规定：对于横向的炮， S S 集合代表选， T T 集合代表不选；对于纵向的炮， S S 集合代表不选， T T 集合代表选，约束条件就直接变成了“不允许一个点在 S S 集合，一个点在 T T 集合”，只需要从前者向后者连一条边权为 ∞ ∞ 的边即可。

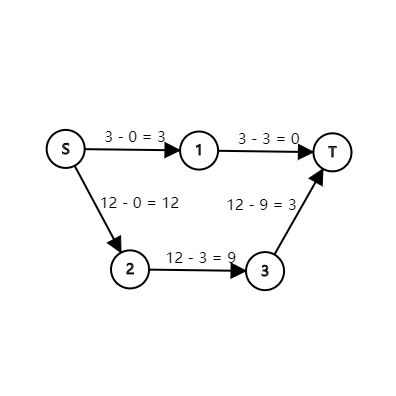
  根据样例再画张图，和上图对比下就懂了。

  上图中最小割为 6 6 ， sum s u m 为 3+12=15 3 + 12 = 15 ，所以答案为 9 9 。

  不难发现点数为 O(n+m) O ( n + m ) ，边数为 O(nm) O ( n m ) ，时间复杂度为 O(Network Flow) O ( N e t w o r k   F l o w ) 。

参考代码

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
typedef long long LL;
typedef unsigned long long ULL;
using std::cin;
using std::cout;
using std::endl;
typedef int INT_PUT;
INT_PUT readIn()
{
    INT_PUT a = 0;
    bool positive = true;
    char ch = getchar();
    while (!(ch == '-' || std::isdigit(ch))) ch = getchar();
    if (ch == '-')
    {
        positive = false;
        ch = getchar();
    }
    while (std::isdigit(ch))
    {
        a = a * 10 - (ch - '0');
        ch = getchar();
    }
    if (positive) a = -a;
    return a;
}
void printOut(INT_PUT x)
{
    char buffer[20];
    int length = 0;
    if (x < 0) putchar('-');
    else x = -x;
    do buffer[length++] = -(x % 10) + '0'; while (x /= 10);
    do putchar(buffer[--length]); while (length);
}

const int INF = (~(int(1) << (sizeof(int) * 8 - 1))) >> 1;
int nVertex;
struct NetworkFlow
{
    static const int maxv = 10005;
    struct Edge
    {
        int from, to, cap, flow;
        Edge() {}
        Edge(int from, int to, int cap) : flow(), from(from), to(to), cap(cap) {}
    };
    std::vector edges;
    std::vector<int> G[maxv];

    void addEdge(int from, int to, int cap)
    {
        edges.push_back(Edge(from, to, cap));
        edges.push_back(Edge(to, from, 0));
        int i = edges.size();
        G[from].push_back(i - 2);
        G[to].push_back(i - 1);
    }

    int s, t;

    int level[maxv];
    int cur[maxv];
    int DFS(int node, int opt)
    {
        if (node == t || !opt) return opt;
        int flow = 0;
        for (int& i = cur[node]; i < G[node].size(); i++)
        {
            Edge& e = edges[G[node][i]];
            int t;
            if (level[node] + 1 == level[e.to] && (t = DFS(e.to, std::min(opt, e.cap - e.flow))))
            {
                flow += t;
                e.flow += t;
                edges[G[node][i] ^ 1].flow -= t;
                opt -= t;
                if (!opt) break;
            }
        }
        return flow;
    }

    int vis[maxv];
    struct Queue
    {
        int c[maxv];
        int head, tail;
        Queue() : head(), tail() {}
        bool empty() { return head == tail; }
        void clear() { head = tail = 0; }
        void push(int x) { c[tail++] = x; }
        void pop() { head++; }
        int front() { return c[head]; }
    } q;
    bool BFS()
    {
        static int stamp;
        stamp++;
        q.clear();
        level[s] = 0;
        q.push(s);
        vis[s] = stamp;
        while (!q.empty())
        {
            int from = q.front();
            q.pop();
            for (register int i = 0; i < G[from].size(); i++)
            {
                const Edge& e = edges[G[from][i]];
                if (e.cap > e.flow && vis[e.to] != stamp)
                {
                    level[e.to] = level[from] + 1;
                    q.push(e.to);
                    vis[e.to] = stamp;
                }
            }
        }
        return vis[t] == stamp;
    }

    int Dinic()
    {
        int flow = 0;
        while (BFS())
        {
            memset(cur, 0, sizeof(cur));
            flow += DFS(s, INF);
        }
        return flow;
    }
} nf;

const int maxn = 55;
int n, m;
int rect[maxn][maxn];

struct CodeHelper
{
    int x, y;
    int code;
    int sum;
    CodeHelper() {}
    CodeHelper(int x, int y, int code, int sum) : x(x), y(y), code(code), sum(sum) {}
};
std::vector helper;
std::vector<std::pair<int, int> > row;
std::vector<std::pair<int, int> > colum;
int cross[maxn][maxn];

int accum;
void run()
{
    n = readIn();
    m = readIn();
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            rect[i][j] = readIn();

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
        {
            if (rect[i][j] == -1)
                nVertex += i - 1;
            else if (rect[i][j] == -2)
                nVertex += n - i;
            else if (rect[i][j] == -3)
                nVertex += j - 1;
            else if (rect[i][j] == -4)
                nVertex += m - j;
        }
    nf.s = 0;
    nf.t = nVertex + 1;

    for (int x = 1; x <= n; x++)
    {
        int sum = 0;
        for (int y = 1; y <= m; y++)
        {
            if (rect[x][y] > 0) sum += rect[x][y];
            if (rect[x][y] == -3)
            {
                accum += sum;
                row.push_back(std::make_pair(helper.size(), 0));
                for (int i = y - 1; i; i--)
                {
                    helper.push_back(CodeHelper(x, i, helper.size() + 1, sum));
                    cross[x][i] = helper.size();
                }
                row.back().second = helper.size() - 1;
            }
        }
        sum = 0;
        for (int y = m; y; y--)
        {
            if (rect[x][y] > 0) sum += rect[x][y];
            if (rect[x][y] == -4)
            {
                accum += sum;
                row.push_back(std::make_pair(helper.size(), 0));
                for (int i = y + 1; i <= m; i++)
                {
                    helper.push_back(CodeHelper(x, i, helper.size() + 1, sum));
                    cross[x][i] = helper.size();
                }
                row.back().second = helper.size() - 1;
            }
        }
    }
    for (int i = 0; i < row.size(); i++)
    {
        int begin = row[i].first;
        int end = row[i].second;
        nf.addEdge(nf.s, helper[begin].code, helper[begin].sum);
        for (int j = begin; j < end; j++)
        {
            int x = helper[j].x;
            int y = helper[j].y;
            nf.addEdge(helper[j].code, helper[j + 1].code, helper[j].sum - rect[x][y]);
        }
        nf.addEdge(helper[end].code, nf.t, helper[end].sum - rect[helper[end].x][helper[end].y]);
    }

    for (int y = 1; y <= m; y++)
    {
        int sum = 0;
        for (int x = 1; x <= n; x++)
        {
            if (rect[x][y] > 0) sum += rect[x][y];
            if (rect[x][y] == -1)
            {
                accum += sum;
                colum.push_back(std::make_pair(helper.size(), 0));
                for (int i = x - 1; i; i--)
                {
                    helper.push_back(CodeHelper(i, y, helper.size() + 1, sum));
                    if (cross[i][y])
                    {
                        nf.addEdge(cross[i][y], helper.size(), INF);
                    }
                }
                colum.back().second = helper.size() - 1;
            }
        }
        sum = 0;
        for (int x = n; x; x--)
        {
            if (rect[x][y] > 0) sum += rect[x][y];
            if (rect[x][y] == -2)
            {
                accum += sum;
                colum.push_back(std::make_pair(helper.size(), 0));
                for (int i = x + 1; i <= n; i++)
                {
                    helper.push_back(CodeHelper(i, y, helper.size() + 1, sum));
                    if (cross[i][y])
                    {
                        nf.addEdge(cross[i][y], helper.size(), INF);
                    }
                }
                colum.back().second = helper.size() - 1;
            }
        }
    }
    for (int i = 0; i < colum.size(); i++)
    {
        int begin = colum[i].first;
        int end = colum[i].second;
        nf.addEdge(helper[begin].code, nf.t, helper[begin].sum);
        for (int j = begin + 1; j <= end; j++)
        {
            int x = helper[j - 1].x;
            int y = helper[j - 1].y;
            nf.addEdge(helper[j].code, helper[j - 1].code, helper[j - 1].sum - rect[x][y]);
        }
        nf.addEdge(nf.s, helper[end].code, helper[end].sum - rect[helper[end].x][helper[end].y]);
    }

    printOut(accum - nf.Dinic());
}

int main()
{
#ifndef LOCAL
    freopen("cti.in", "r", stdin);
    freopen("cti.out", "w", stdout);
#endif
    run();
    return 0;
}

总结

  最小割模型并不是想象的那样死板，它还是相当灵活的。从这道题看来，你把集合互换一下完全没有影响，还帮你把题给解决了。