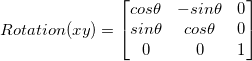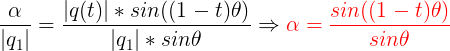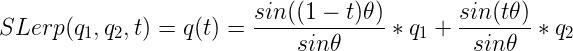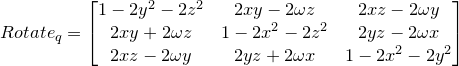Unity 学习笔记：旋转

这篇文章归纳一下Unity中的坐标变换以及四元数的相关用法，这是Unity中的基础也是重点，最近查了网上很多的博客和看了一些书籍，觉得是时候有必要把看过的这些东西归纳起来了。

引子：

对于一个向量来说，我们可以使用一个复数来表达一个它，我们可以认为一个复数将一个向量分量与其他的向量分量驱隔开来，例如一个二维向量(x,y)=x+yi；三维向量(x,y,z)=x+yi+zj；

对于复数的乘法，符合如下规律：

                   

                                                 

                                                 

最后我们可以用矩阵来表示这个乘法，我们在下文中的叉乘的矩阵形式还能看见它，如果你看见一个向量运算转为矩阵运算有点不知所措的时候，可以从复数来想想推导的思路。

---

二维平面的旋转

我们首先从二维平面说起，我们首先设定，我们的旋转是在右手坐标系下的右手（逆时针）旋转（这句话非常关键）。如果你发现你计算时有什么不对的话（比照别人的结果正负存在差异），就应该用右手去比对坐标轴的方向看看是不是旋转的手性问题。

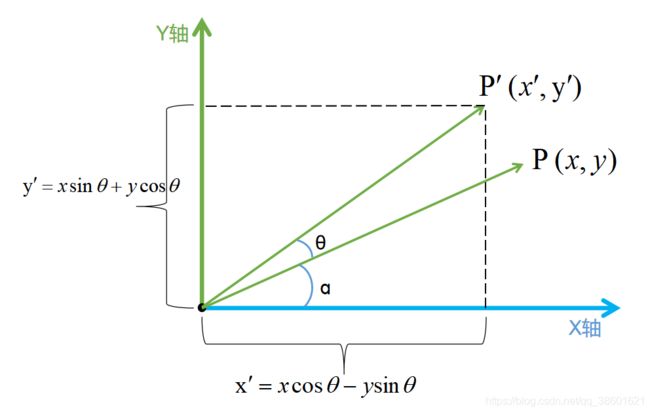
如图，存在于XY平面上的向量P(x,y)绕着中心点旋转，那么这个向量来说，如果我们逆时针旋转一定的角度θ，那么对于旋转后的向量P'(x',y')存在如下的关系：

对于P点来说，它与X轴的夹角为α，那么P'点与X轴的夹角为θ+α，那么对于P的XY分量和P'的XY分量有如下的计算：

                            

                            

                                                                      

                            

所以对于P'来说，我们可以知道它的XY分量为：

                           

                            

复数形式的P'：我们可以将P'向量用复数形式表达出来，那么此时的P'存在实部与虚部：

                         

                               

                               

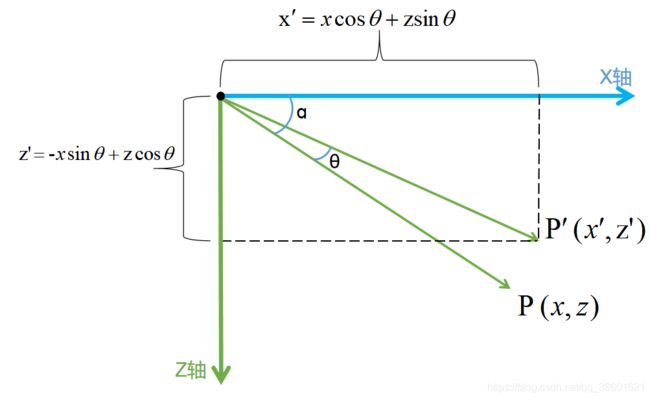
我们可以看到，此时P'分为了两个复数，分别代表（x，y）向量和（-y，x）向量。对应到图像上，即为P向量和与P向量垂直90°的向量P⊥。我们可以在图像上看到它们：

此时我们可以推导出P'用P向量和P⊥向量表达的结果： 

                                                                        

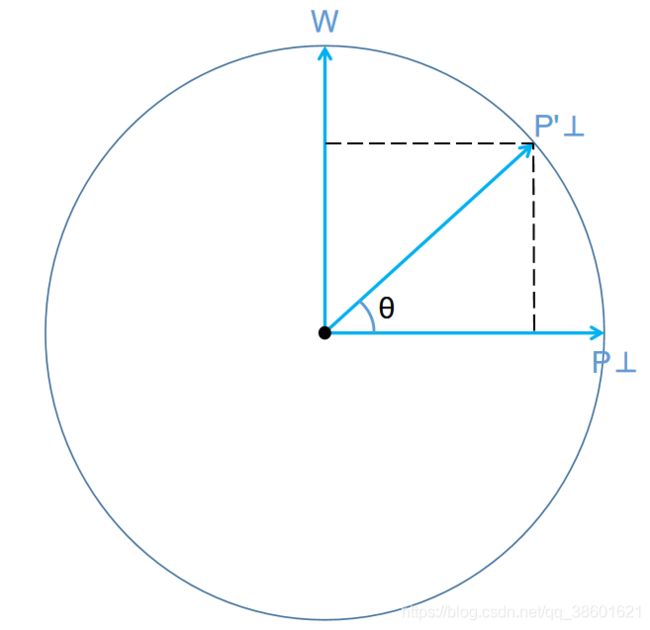
矩阵形式的P'：同时，我们可以将上文中的XY分量写成矩阵形式，即在二维平面下向量P旋转θ角过后的P'为：

                          

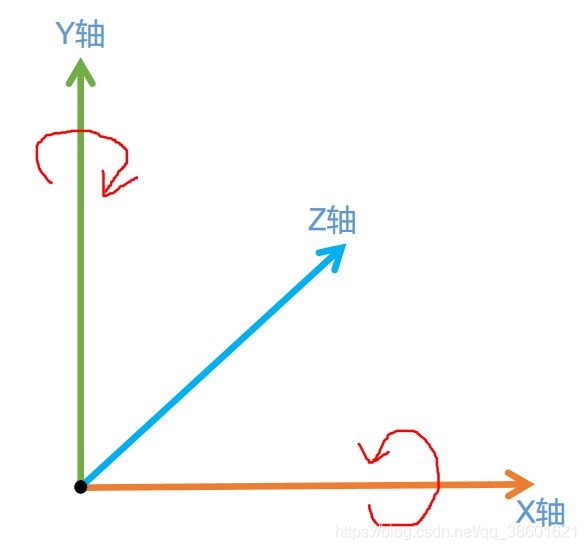
我们在大脑中将上面那张图扩充到三维空间中，在XY平面逆时针旋转实际上就是在三维右手坐标系中围绕Z轴旋转的样子。那么我们可以将上文中的矩阵扩充到3X3矩阵。得出XY平面绕Z轴的旋转矩阵和YZ平面绕X轴的旋转矩阵，它们的Z轴和X轴都扩充为单位矩阵的值，意味着在乘以矩阵后不变：

                                                    

XZ轴绕Y轴旋转的矩阵推导：我们需要注意到旋转矩阵的坐标系和旋转的旋向性都是右手（不然你就会像我一样冥思苦想几个小时），所以对于XZ轴绕Y轴旋转的情况与上面有所区别，我们如果要让向量在屏幕这个平面上的右手坐标系表现逆时针旋转，就需要让大拇指（X轴）和和中指（Z轴）平行于屏幕，此时的食指（Y轴）应该指向屏幕面前的你自己，根据这个情况我们可以画出关于XZ平面围绕Y轴旋转的图像：

我们计算这种情况下的Z轴，此时的P'点与X轴的夹角为α-θ，那么相应的P'的XY分量和P'点的坐标为：

                        

                            

                        

                            

那么XZ平面围绕Y轴旋转的旋转矩阵为：

                        

此时我们已经推导出了Unity常用的三个旋转矩阵，我（不知道这样说对不对）把这三个矩阵称为欧拉角矩阵，我们可以看到这个旋转非常的直观简单，但是它的由来并不简单，如果你是一个数学带神的话，有许多中方法能得出这个公式，例如泰勒展开等等，并且，它也可以用来推导欧拉公式。我数学并不好，这里选用了一个比较基础的推导方法来表示二维的旋转。在Unity的Transform组件中，手动调整Rotation数值即为欧拉角的旋转，这三个旋转矩阵也是下文推导三维旋转方法的基础。

---

三维空间的旋转

虽然上文已经给了三个三维空间旋转矩阵，但是很明显它们都是根据基轴旋转而来的，这样的单纯的旋转显然不能满足我们的需求，三维空间中，我们要求的旋转为轴角式的旋转：让任意的向量P围绕任意的向量A右手旋转θ度，其中，由于向量A不需要长度，我们可以认为它为只表示方向的单位向量（模长为1）。

我们在上文中已经把二维的旋转分解成了映射在两个基轴的向量，同样的，这里也需要将向量P分解为：与向量A平行的向量P//和与向量A垂直的向量P⊥（不知道这算不算分治法的应用？），我们画一个图来表示它们的关系：

并且，P与向量P⊥和向量P//的关系为：P = P// + P⊥。我们分别来看两个分量的关系：

P//实际上是向量P在单位向量A上的投影，并且A为单位向量，模长为1，则P为：

                    

                    

并且根据上面的关系，则P⊥为：

                     

注意，我们这里只是进行了分解，并没有进行旋转，如果我们围绕向量A旋转向量P旋转θ角，那么上面的图像此时为：

此时我们可以知道，所谓的向量P围绕向量A的旋转，实际上是分量P⊥在自身所在平面的圆上旋转，P//动都不带动的，所以此时我们只需要单独分析P⊥就好。那么我们俯视这张图，让向量A垂直于电脑屏幕，上面这张图可以转化为：

为了我们运算方便，我们在上面增加一个辅助轴：W。那么很显然，我们这里从P⊥到P'⊥就变成了二维平面中的向量旋转问题。自然可以轻松的带入上文中的旋转公式。并且，由于辅助轴W在设定时就垂直于P⊥和向量A，所以可以使用P⊥和向量A叉乘而来。即：

                   

                           

                           

                           

                           

由于叉乘遵守乘法的交换律，并且AxP//=0，所以最终旋转θ角后的P'⊥就如同上面写的那样。我们既然获得了旋转后的P垂直，那么我们也可以推导出旋转θ角后的向量P，并稍微进行一些调整：

                    

                           

                           

此时，我们已经得出了向量P围绕单位向量A旋转θ角的公式。这个式子是推导四元数的旋转的基础。

---

四元数

四元数我们可以认为是一个四维空间向量(x,y,z,w)，在引子中，我们写出来了二维向量和三维向量的复数形式，我们根据它们可以写出四元数的复数形式，即对于一个四元数Q来说：

                       

同时，它也可以写成q=ω+v（下文中我都默认把实部放在前面了），其实就是将虚部转换成一个向量v=(x,y,z)。同样的，任何三维的向量也可以转换为一个四维向量（想象这个向量处于一个四维空间的三维子空间上就好），我们将这个三维空间的实部设为0，那么就可以将一个三维向量转换成四维向量（四元数），存在：

                       

我们将实部(ω)为0的四元数称为纯四元数，上面的Qv即为纯四元数，并且四元数存在如下的性质：

1.四元数的三个复数：四元数的三个复数ijk的平方之和为1，三个复数ijk的积为1，即：

                        

2.四元数的模长：和三维向量的模长计算方法相似，即：

                       

并且对于单位四元数来说，存在模长为1，即|Q|=1。这和三维向量是一致的。

3.四元数乘法：四元数的加减法即为实部与实部相加，虚部与虚部相加（这里和其他复数一致），但是对于乘法来说，它不满足交换律，并且运算过程非常奇妙。我们这里假设两个四元数相乘，然后将结果按照三个虚部与实部摆放好（这里省略掉了一些中间的过程）：

                   

                                

                                

                                

并且对于两个四元数的虚部（即为各自对应的三维向量，我们假设它们叫v1和v2），存在基本的点乘叉乘：

                     

                   

那么对于四元数q1和q2来说，我们可以发现，四元数乘法后实部为两个四元数的实部乘积减去虚部的点乘，虚部为两个四元数实部与虚部的交叉乘积减去两个四元数虚部的叉乘。即为下面的这个四元数的积：

                   

这个积非常重要，我们可以使用它来推导出四元数非常多的性质。例如，两个纯四元数的乘积为：

                   

4.共轭四元数：对于四元数来说，它和基本的复数一样存在共轭：

                     

并且对于四元数和它的共轭来说，它们的乘积为：

                         

                                    

                                    

5.四元数的逆数：于四元数来说，存在四元数的逆数：

                     

并且对于单位四元数来说，单位四元数的逆数和单位四元数的共轭存在如下关系：

                            

现在我们已经大致的了解四元数的一些性质了，四元数的乘是大部头，也是最需要整明白的地方，我们接下来将四元数运用到我们上面推导出来的轴角的公式上。 

---

将四元数运用到旋转

我们照搬一下上文中的旋转公式，对于我们的旋转来说，向量P围绕向量A旋转θ角度可以由分量P//和P⊥得出：

                               

我们此时引入四元数，将上文中的所有的三维向量都变成纯四元数，为了与上文中的三维变量有所区分，我们将所有字母改为小写，例如三维向量A转换成纯四元数a：

                                  

其他的向量们也如法炮制，然后我们回到P⊥上（毕竟它才是真正在运动的向量），此时P⊥已经是一个纯四元数了，但是公式仍然没变：

                               

此时，A叉乘P⊥用四元数来表示，它们有如下转换关系：

                         

所以此时我们的p'⊥可以表示为：

                                

我们可以惊讶的发现，此时的红色部分就已经是一个四元数了（我第一次看的时候觉得神奇得不行），它符合四元数的规则，并且独立于P向量和它的分量之外，我们拎出这个“带明星四元数”，称它为Q：

                                                    

既然我们已经得到了旋转以后的p'⊥，我们可以进一步得到结果：

                                                                        

此时，为了得出最终的结果，我们需要引入三个引理：

引理1：对于四元数Q来说，存在：

                                  

这个引理可以使用四元数的乘法推导出来：

                             

                                          

                                         

我们将上文中得到的四元数Q倒推回去，得到：

                                 

此时我们将上文中的代码引入到p'的公式上，那么上文中的p'变成了：

                       

实际上，这句话的几何意义为：如果一个向量P围绕向量A旋转θ角度时，P//不变，而P⊥旋转了两次θ/2角度，最终旋转一个θ角度。
为了得到最终的三维四元数旋转公式，我们还需要引入两个引理：

引理2：对于四元数q:(ω,a)来说，让q乘以与向量a平行的纯四元数v，存在：q * v = v * q：

                   

                   

引理3：对于四元数q:(ω,a)来说，让q乘以与向量a垂直的纯四元数v⊥，存在：

                      

                      

我们此时根据这两个引理，我们可以将上文中的p'次进一步推导：

                                   

                                         

                                        

并且，p//与p⊥相加就等于初始情况下的p，所以我们可以推导出最终的三维旋转四元数公式：

四元数的三维旋转公式：向量P围绕单位向量A旋转θ角得到P存在': 

 

                                   

此时我们已经得到的四元数的一个公式，这个公式可以推导出来任何一个角度的旋转轴，并且p'和p都是纯四元数。

并且这个四元数q为单位四元数，我们可以简单地推导一下：

                                     

 对于四元数的旋转公式，它同等于如下的式子

                                     

四元数三维旋转公式的性质：

 1.四元数的三维旋转公式也被称为同态函数，在旋转后能保证旋转后向量的角度不变性、手性不变性，即：

                                

2.任意标量乘以四元数q都表示相同的旋转操作，例如四元数乘以一个数值x，那么有：

                               

---

为什么要使用四元数来表达旋转

我们在上文中已经写了三种旋转矩阵的写法，分别是二维平面的旋转，三维空间的旋转。四元数的旋转，看起来它们的关系是层层递进的，其实包括我自己写到这里的时候犯嘀咕，为啥我们需要多引入一个量来表示旋转呢，我们使用前面的一些矩阵就已经非常清晰的表示旋转了，四元数看起来像是“画蛇添足”。有一说一，确实，相较于其他的旋转方法，四元数一点也不直观，而且四元数比较难，我刚开始看的时候觉得我这辈子都搞不明白这个，你可以看到上文中关于四元数的章节我一张图都没有，因为确实不好表示（我数学本来就不好，高考的时候几何大题都空着），但是相较于其他的旋转方式来说，四元数有它独到的地方，我们分为三个方面来论述这个原因，前两个方面论述其他的旋转方法的缺点，后一个方面论述四元数旋转的优点：

1.万向节锁

对于欧拉角来说，存在三个基轴进行旋转，对于这种情况下的旋转，Unity常常用上文中的三个旋转矩阵的组合来表示分别对三个轴进行的旋转，例如我们一次性要用欧拉角（θx，θy，θz）来进行多次旋转，那么实际上Unity内部实际上是ZXY的顺序来表示三个轴的旋转，并且由于每次欧拉旋转后改变旋转轴，最终的旋转的矩阵实际上是YXZ：

                    

这样看起来很美好，当我们使用Transform组件时，如果我们将一个物体旋转，只需要将某个轴的旋转带入上面的矩阵就完事了。但是事情总是不会那么顺遂。

欧拉角里面存在一个问题叫做万向节锁（Gimbal Lock），在使用欧拉角旋转的时候如果将一个特定的轴旋转90°（我隐隐觉得这个轴就是三个旋转矩阵的中间那个矩阵对应的轴，例如Unity中这个中间轴为X），那么在旋转的时候就很可能会出现某个轴被“锁住”的情况。这个锁住我自己描述为：万向节锁时单一的旋转某个轴分量可能得不到对应的旋转结果。

例如我们上文中旋转的例子，我们将X轴旋转90°，那么上文中的矩阵就转为：

                   

                                                   

                                                   

这里从式子上看九很明显了：无论此时的点（x，y，z）如何旋转任何θy或θz角度，左乘Rotate(90,θy,θz)最终都不能导致Y轴旋转量的变化。具体到Unity中，我们就能看到当x旋转90度后，改变y轴的旋转量不能让物体围绕此时的y轴旋转（围绕图中绿色的轴旋转），而是旋转摊到了其他轴上，如下图，单纯的改变Y轴并不能获得正确的旋转结果：

究其原因，实际上是因为从欧拉角到旋转的映射并不是一个覆盖映射，即它并不是在每个点处都是局部同胚的（这里引用维基上的说法）。我在这里不做深入解释，因为我也不懂（我是渣渣），但是我们留个引子在这里，某一天也许我开窍了能写下去。对于某一个顺序的欧拉角的时候，夹在中间的那个角度如果设置为π/2，那么很容易就发生万向节锁。

虽然Y轴陷入了困境，但是我们手动去调整可视化的旋转，最终还是能解决万向节锁的问题（图里面已经演示了），但是在内部，则是通过四元数的球面插值来解决这个问题。对于轴角式的旋转和四元数的旋转来说则不存在这种问题。

2.多次旋转

一个向量往往不止旋转一次，很多时候有多次不同角度，不同轴的旋转，那么对于这些旋转方法来说提出了要求。

轴角的多次旋转：

我们可以看到三维空间中的轴角非常的好用，它能实现任何角度的任何旋转并且非常直观，没有万向节锁的问题。但是我们在最终在代码或者程序中应用的时候并不是上文中那个公式，而是根据缩放和平移的需要将轴角公式转换成了一个矩阵，即：

            

                 

                 

这里我们运用到了一些向量的矩阵乘法来进行计算，来将这个公式尽量化成矩阵形式，这里用到了叉乘的矩阵写法，即：

     

然后我们再将上面的矩阵形式最终整合到一起，可以表达出轴角的矩阵形式，我们用C = cosθ、S = sinθ，即当围绕向量A旋转θ角度时：

                        

     

这个矩阵形式已经非常堪用了，我们能用它来求各种各样的轴角旋转。但是如果我们对于每个向量进行多次旋转的时候，它的问题就显现出来了，我们可能要让两个3x3矩阵相乘。假设这里要围绕A轴旋转θ1度，围绕B轴旋转θ2度，那么我们需要如下计算：

                         

四元数的多次旋转：

当一个向量旋转一次，那么就要乘以对应的四元数q1，如果我们此时需要再次旋转一次，就需要乘以另一个四元数q2，然后将q1*q2的结果带入四元数公式就好了，即为：

                         

此时问题就显现出来了，四元数在进行多次旋转的时候，q1*q2需要16次的乘加运算（等式右边的逆数直接共轭就好了），而对于轴角矩阵的多次旋转的情况来说，Rotate(θ1)*Rotate(θ2)需要27次的乘加运算，此时四元数的优势要大得多。所以因为运算量的差异，也使得我更觉得四元数要运算简单一些。

3.旋转的插值

我们上文（也没多上）中提到过遇见万向节锁时候，，Unity内部通过四元数的球面插值来解决问题。四元数最强的地方就在这里：能够做到旋转的插值。在四元数的插值中：旋转的插值往往就是两个四元数的插值，然后用插值后的四元数带入旋转公式来计算。听起来很简单，但实际上四元数的插值存在两种方式：

线性插值：

线性插值非常简单，因为我们已经在Shader的文章中用过多次了，在四元数的插值中，同样存在线性插值的方法，对于四元数线性插值的结果q(t)来说，四元数存在以下的线性插值：

1.沿线段的线性插值Lerp：当我们单纯将四元数的带入线性插值公式，就能得到q(t)等于q1和q2的连线上的四元数，就会得到这样一个公式：

                       

2.沿弧度的线性插值NLerp：此时的四元数还只是沿着线段插值，如果我们需要得到圆弧上移动的四元数插值，就需要将四元数除以它的模长，这种方式称为正规化（Normalized）线性插值（是不是很像求单位向量？），即：

                   

它们二者在图像上存在如下的关系（为了我们大脑能够接受，我们将四元数画成向量的样子）： 

但是这种弧度插值的方法也存在一定问题，由于q(t)会随着t的值从0-1变化由快到慢再到快（t=0.5时最快），所以随着t的变化q(t)并不是平滑的移动，所以我们需要使用q1和q2的角度插值。

3.沿角度的球面插值SLerp： 

如果我们需要根据角度来插值来让一个四元数在一个弧面上平滑的移动，所以这种方法称为球面（Spherical）插值。它需要在q1和q2进行线性插值的时候，将q(t)在q1和q2之间的圆弧上变化速率变为常数，我们假设q1到q2旋转θ度，那么随着t的变化，q(t)在夹角上移动，，对于插值来说，存在：

                           

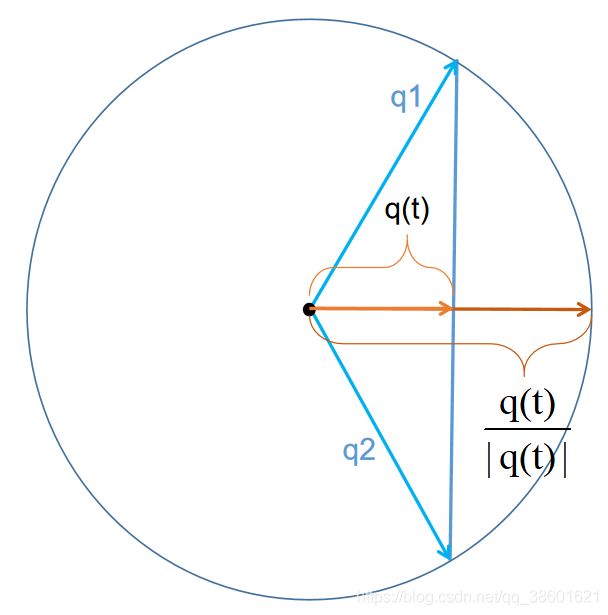
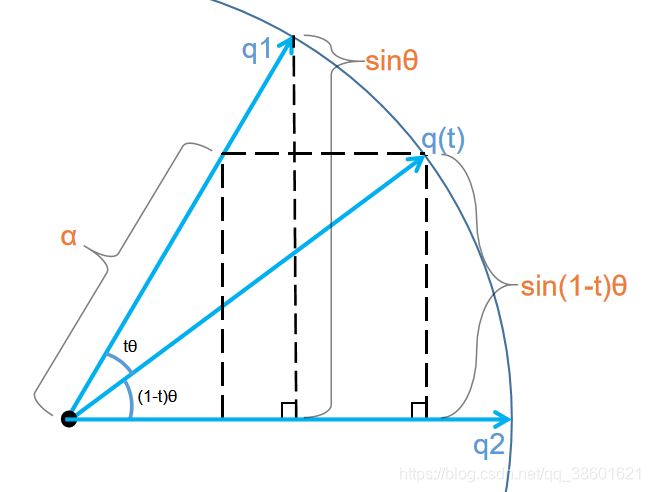
此时的α和β是我们人为标定的两个系数，可以代表q1和q2在q(t)中的比例，同时在几何上，α代表q(t)沿q1方向分量的长度，β代表q(t)沿q2方向分量的长度 ，我们可以根据图像分别对α和β进行计算。

α：对于α来说，α和q1的比例等于q(t)到q2垂直距离与q1到q2垂直距离的比例，如图：

我们可以根据图像获得式子，同时，由于旋转的时候接触到的四元数都是单位四元数，所以这些四元数长度通通为1，所以我们可以“轻松”地获得α的值：

                            

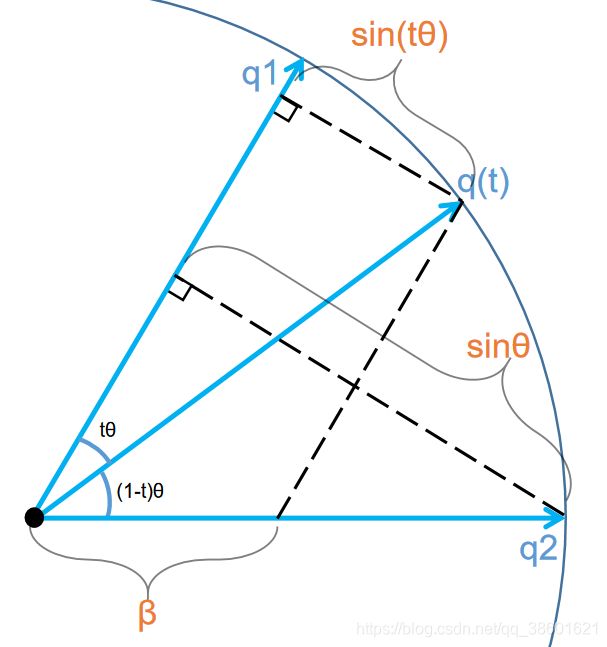
β： 对于β来说同理，β和q2的比例等于q(t)到q1垂直距离与q2到q1垂直距离的比例，如图:

同样的可以根据图像获得式子：

                              

最终我们就能得到球面线性插值的公式，即：

                            

这样我们就能非常方便的在两个旋转策略上插值了，哇，这看起来好方便~（棒读）。

球面插值的问题：

虽然球面插值比正规化线性插值要准确一些，但是效率并不太好，所以如果我们的两个插值的四元数的夹角并不是很大的情况下，我们直接使用NLerp就好了。

并且，如果当两个四元数的夹角特别小（小到接近0）的时候，可能会导致除以0的错误，所以夹角过小的时候，也最好使用归一化线性插值来代替球面插值，因为这个时候二者的插值的速率区别已经完全看不出来了。

---

旋转的应用

我们上面好像全都在写各种各样的算式，但无论计算方法多么高深，还是要落在代码中，在这一篇文章的末尾，我们写两个镜头脚本，来简单的运用一下旋转（来简单的凑一下字数）。

在Unity中，虽然四元数很重要，但是往往在操控的时候输入的内容为欧拉角或轴角，我们几乎不会亲自去调整四元数的四个分量。我们写一个非常基础的镜头操控脚本，我们通过获得当前屏幕平面鼠标的的X轴和Y轴旋转量来旋转我们的代码。我们需要注意：

• 鼠标沿屏幕上的平行移动（X轴移动）需要对应到欧拉角的Y轴分量。因为它实际上在操控物体的Y轴旋转。
• 鼠标沿屏幕上的垂直移动（Y轴移动）需要对应到欧拉角的X轴分量。因为它实际上在操控物体的X轴旋转。
• 由于世界空间使用左手坐标系的左手旋转，那么对于垂直移动来说：鼠标上移的值为正，镜头往下移动，鼠标下移的值为负，镜头往上移动，这与我们平常使用的习惯相反，所以一般可以将Y轴旋转量设为负数。

我们画一个图来表示左手坐标系左手旋转的欧拉角XY轴实际旋转的方向：

最终我们可以写一个在Game界面中模拟Scene界面操控的代码。在代码中，使用欧拉角的四元数形式对镜头的旋转进行操控，并使用物体本身旋转的欧拉角eulerAngles的四元数形式对位移向量的方向进行操控，来模拟Scene的效果：

using UnityEngine;

public class ShaderCamera : MonoBehaviour
{
    private float XX;
    private float YY;

    [Header("运动速度")]
    public float MoveSpeed=2.5f;

    [Header("镜头移动速度")]
    public float CameraSpeed=1f;

    void FixedUpdate()
    {
        float V = Input.GetAxis("Vertical");
        float H = Input.GetAxis("Horizontal");

        if(Input.GetMouseButton(1))
        {
            float xx = Input.GetAxis("Mouse X")*CameraSpeed;
            float yy = Input.GetAxis("Mouse Y")*CameraSpeed;
            XX += xx;
            YY += yy;
            this.GetComponent().rotation = Quaternion.Euler(-YY, XX, 0);
        }
        if(Input.GetKeyDown(KeyCode.LeftShift))
        {
            MoveSpeed += 5;
        }
        if(Input.GetKeyUp(KeyCode.LeftShift))
        {
            MoveSpeed -= 5;
        }

        this.GetComponent().velocity = Quaternion.Euler(this.transform.eulerAngles) * new Vector3(V, 0, H) * MoveSpeed;
    }
}

最终我们可以使用这些旋转模拟出Scene脚本的自由移动效果。说实话挺糙的，不过能用。

---

哇，这篇文章我足足写了一个星期，一个星期以前我连四元数是啥都不知道。。。。唉，太惨了，如果我不这么菜就好了，这篇文章实际上对很多地方比较浅，我也不敢说都搞懂了，例如欧拉角的许多性质实际上都是泛泛而谈，不敢说自己比较熟（本文没有说到欧拉公式），并且，对于很多地方的推导自己可能也没有达到很精通的地步，毕竟我数学太差了（小时候三四年级的时候连100以内加减法都不会）。我一年前，曾经问过学校的某位老师啥叫四元数，结果他张口来了一句“复变函数”，这让我感觉就像大海捞针一样，并且我在网上很多地方翻阅都发现四元数讲得很浅，这实际上是对四元数的理解很不利的，对于某个知识来说，我们只能知道一个点却不能把它连成片的话，那么这个点也会随着时间消失掉，最后在点上花的时间也会变成无用功。

如果让我现在来看四元数，我很愿意将它理解为一种“降维打击”，通过四维空间的向量就能很轻松的表达三维空间中的旋转问题，并且能获得诸多的方便，但是它在三维空间中的使用也是要根据二维空间一步步推导出来的。这也是我为啥要从二维平面的图像开始写的原因。在Unity中的具体应用中，四元数实际上已经包装成了一个黑盒，但并不代表我们就可以忽略掉四元数的使用。

参考：

这篇文章参考了网上很多大神的理解，然后自己加了一丢丢私货进去，如果您有地方不太懂的地方我非常愿意和您讨论，我看到了一定会回复（这是精进的途径）。并且这篇文章的起因是我最近翻了一下《3D游戏与计算机图形学的数学方法》，这本书很棒，除了根本不给推导以外，其他的挺面面俱到的。

《3D游戏与计算机图形学的数学方法》第四章：坐标变换

https://link.zhihu.com/?target=https%3A//krasjet.github.io/quaternion/（这篇文档写得超好，我这种小白也能看懂，真的感谢！）

https://zhuanlan.zhihu.com/p/45404840

https://blog.csdn.net/candycat1992/article/details/41254799

附录：四元数的矩阵写法

由于在代码中还存在缩放矩阵和用于移动的齐次矩阵，所以我们有时候可能需要将四元数转换成轴角矩阵的写法来配合其他的操作，它从轴角的公式推导而来，即

                     

                     

由于q为单位四元数，存在：，所以，上述的例子中的第一个矩阵的值可以修改为：

       

依照上面的例子，我们可以将这三个矩阵组合起来，最终就能得到四元数的矩阵形式：