【小白打造编译器系列3】实现简单的公式计算器（加法和乘法）（JAVA实现）

我们在前文【小白打造编译器系列1】编译器的前端技术是什么？已经知道语法分析的结果是生成一个 AST。那么我们通过实现一个简单的公式计算器来加深对生成 AST 过程的理解。本文的重点是：递归下降算法 和 上下文无关文法。我们讲解只考虑 加法 和 乘法。（减法和除法原理上是一样的，这里就不重复讨论了）

---

原理详谈

变量声明语句

我们先来看看变量声明语句，理解什么是“下降”。

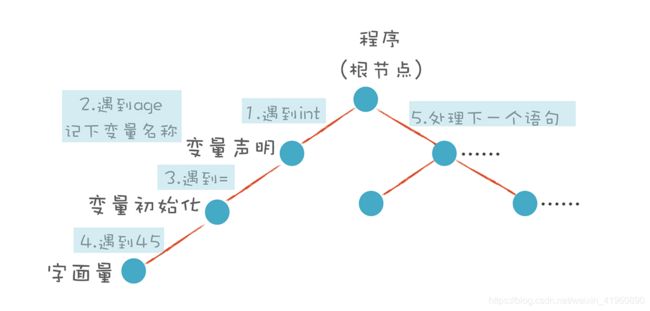
之前提到过了，对于 “int age = 45” 这种声明语句，我们构建的 AST 如下所示。

声明变量语句的规则： 它的左边是一个 非终结符（Non-terminal）。右边是它的 产生式（Production Rule）。在语法解析的过程中，左边会被右边替代。如果替代之后还有非终结符，那么继续这个替代过程，直到最后全部都是终结符（Terminal），也就是 Token。只有终结符才可以成为 AST 的叶子节点。

对于int 类型变量的声明，需要有一个 Int 型的 Token，加一个变量标识符，后面跟一个可选的赋值表达式。想要匹配一个 int 类型的变量声明语句，伪代码如下。

//伪代码
MatchIntDeclare(){
  MatchToken(Int)；        //匹配Int关键字
  MatchIdentifier();       //匹配标识符
  MatchToken(equal);       //匹配等号
  MatchExpression();       //匹配表达式
}

 而用JAVA实现起来，具体代码如下。这里使用了Token流，来对Token进行预读与读取操作。

SimpleASTNode node = null;
Token token = tokens.peek();    //预读
if (token != null && token.getType() == TokenType.Int) {   //匹配Int
    token = tokens.read();      //消耗掉int
    if (tokens.peek().getType() == TokenType.Identifier) { //匹配标识符
        token = tokens.read();  //消耗掉标识符
        //创建当前节点，并把变量名记到AST节点的文本值中，
        //这里新建一个变量子节点也是可以的
        node = new SimpleASTNode(ASTNodeType.IntDeclaration, token.getText());
        token = tokens.peek();  //预读
        if (token != null && token.getType() == TokenType.Assignment) {
            tokens.read();      //消耗掉等号
            SimpleASTNode child = additive(tokens);  //匹配一个表达式
            if (child == null) {
                throw new Exception("invalide variable initialization, expecting an expression");
            }
            else{
                node.addChild(child);
            }
        }
    } else {
        throw new Exception("variable name expected");
    }
}

这整个匹配声明语句的过程：

解析变量声明语句时，我们先看第一个 Token 是不是 int。如果是，那就创建一个 AST 节点，记下 int 后面的变量名称，然后再看后面是不是跟了初始化部分，也就是等号加一个表达式。我们检查一下有没有等号，有的话，接着再匹配一个表达式。

而所谓的“下降”指的是：上级的算法调用下级的算法。表现在生成 AST 中，上级算法生成上级节点，下级算法生成下级节点。

更直观一点，我们还是在之前那个可视化网站看看，到底一个赋值语句生成了一个怎样的 AST 树节点。

对于 “int age = 45” ，我们生成的节点如下。

算术表达式

实际上前文的变量声明语句的文法并没有离开正则文法，使用正则文法完全可以解决。但是接下来的 算术表达式就不能直接使用正则文法，而是应该使用 上下文无关文法。

我们知道，对于算术表达式（只考虑加法和乘法），我们定义规则就比较麻烦了，因为他们的组合实在是太多了：

• 4 + 6
• 4 + 6 * 5
• 6 * 5 + 4
• 6 * 5
• .......

同时，由于算术符号的优先级不同，我们不能直接使用固定化的正则文法解决。

解决优先级的问题

首先要考虑怎么解决算术表达式的优先级，也就是 “先乘除，后加减” 的问题。在解决这个问题之前，我们必须明确 AST 是怎么计算结果的。

AST 计算过程：从根节点除法，进行深度优先遍历，然后逐步返回下层计算的值。

如下图中，先计算最下层的节点（最深的节点）：3 × 5 = 15，然后把 15 返回到加法的右节点，计算 15 + 2 = 17。

对此，我们想要完成优先级，只需要把乘法（除法）节点作为加法（减法）的子节点即可！从而进行深度优先遍历时，会先计算乘法，再回到加法节点完成加法。

我们仔细来看看下面“嵌套”的文法。在加法表达式的文法中，由于乘法的优先级更高，所以我们可以嵌套一个乘法表达式的文法 ，同时一个加法表达式可以看作一个加法表达式加上一个乘法表达式，通过这种嵌套的方法，我们可以仅通过两条嵌套的规则去匹配所有复杂的加法表达式。可以理解为递归，或者学过算法的朋友可以理解就是动态规划中的中间过程。

举个例子：

• 对于 2 × 3 这种表达式：只需要调用 additiveExpression 中的 multiplicativeExpression。
• 对于 2 + 3 × 5 这种复杂的表达式，调用的规则就是 additiveExpression Plus multiplicativeExpression。

只要能完成这种简单的拆分，无论以后遇到多长的加法乘法算术式，都能拆分成这两种形式。这就是递归的魅力。

additiveExpression
    :   multiplicativeExpression
    |   additiveExpression Plus multiplicativeExpression
    ;

multiplicativeExpression
    :   IntLiteral
    |   multiplicativeExpression Star IntLiteral
    ;

直观的表示如下。

有了这个认知，我们在解析算术表达式的时候，便能拿 加法规则去匹配 。在 加法规则中，会嵌套地匹配乘法规则 。我们通过文法的嵌套，实现了计算的优先级。应该注意的是，加法规则中还递归地又引用了加法规则。

这种文法已经没有办法使用正则文法了，它比正则文法更加具有普适性，表达能力更强，称为：上下文无关文法 。正则文法是上下文无关文法的一个子集。它们的区别就是上下文无关文法允许递归调用，而正则文法不允许。上下文无关的意思是，无论在任何情况下，文法的推导规则都是一样的。比如，在变量声明语句中可能要用到一个算术表达式来做变量初始化，而在其他地方可能也会用到算术表达式。不管在什么地方，算术表达式的语法都一样，都允许用加法和乘法，计算优先级也不变。

TIPS：上下文无关文法其实就像俄罗斯套娃一样，每一层需要讨论的情况都是相同的，将一串很长很复杂的式子进行拆分，最终由简单的乘法和加法构成。下图的表达式是 a = 2 + 9 * 8 + 2 + 4 * 5 * 1 。一长串的加法乘法算术表达式，最终逐层细分下去，最后到叶子节点仅仅只是由简单的 二元加法 和 二元乘法 来表示。（我很尽力表述了）

解决左递归出现死循环问题

OK，到目前为止，我们已经知道了，使用允许嵌套的 上下文无关文法 进行递归就可表示任何一个加法乘法算术式。我们的思路是很对的，那实现起来没有问题吗？当然不是！

我们先看看一个简单的加法的递归： 2 + 3。

additiveExpression
    :   IntLiteral
    |   additiveExpression Plus IntLiteral
    ;

依据上面的文法，我们来分析一下匹配的过程：

• 首先看看是不是字面量，发现 “2 + 3” 是一个加法算式；
• 看看是不是一个加法算式，发现确实是，进行递归；
  • 再看看是不是字面量，发现不是；
  • 再看看是不是加法算是，发现确实是，再次递归
    • .....
    • .....

发现了吗，我们不断地递归并没有解决问题呀，一个简答的加法算式一直递归调用自己。这种情况就是 左递归。通过上面的分析，我们知道 左递归是递归下降算法无法处理的，这是递归下降算法最大的问题。

怎么解决呢？把“additiveExpression”调换到加号后面怎么样？我们来试一试。

也即是说，之前我们讨论的加法的情况是站在加号前面讨论的，这样的递归无休无止。如果我们按照 加号 作为加法算术式的分割符，将算术式一分为二，加号前面的进行递归，加号后面的也进行递归，就可以完美解决问题了。我们反过来继续看看 2 + 3 的例子：

• 加号前：调用 multiplicativeExpression
  • 发现是 IntLiteral ：2
• 加号后：调用 multiplicativeExpression
  • 发现是 IntLiteral ：3

很好的解决了死循环的问题。

additiveExpression
    :   multiplicativeExpression
    |   multiplicativeExpression Plus additiveExpression
    ;
multiplicativeExpression
    :   IntLiteral
    |   multiplicativeExpression Star IntLiteral
    ;

我们先尝试能否匹配乘法表达式，如果不能，那么这个节点肯定不是加法节点，因为加法表达式的两个产生式都必须首先匹配乘法表达式。遇到这种情况，返回 null 就可以了，调用者就这次匹配没有成功。如果乘法表达式匹配成功，那就再尝试匹配加号右边的部分，也就是去递归地匹配加法表达式。如果匹配成功，就构造一个加法的 ASTNode 返回。（原文来源：编译原理之美）

表达式求值

这里就不细谈了，深度优先遍历完整个 AST ，算出根节点的值就是表达式的值。

关键代码实现（完整代码见文末）

加法乘法实现

    /**
     * 语法解析：加法表达式
     * @return
     * @throws Exception
     */
    private SimpleASTNode additive(TokenReader tokens) throws Exception {
        //先加号前面匹配乘法
        SimpleASTNode child1 = multiplicative(tokens);
        SimpleASTNode node = child1;

        Token token = tokens.peek();
        if (child1 != null && token != null) {
            if (token.getType() == TokenType.Plus || token.getType() == TokenType.Minus) {
                token = tokens.read();
                SimpleASTNode child2 = additive(tokens);
                if (child2 != null) {
                    node = new SimpleASTNode(ASTNodeType.Additive, token.getText());
                    node.addChild(child1);
                    node.addChild(child2);
                } else {
                    throw new Exception("【乘法表达式错误】：需要补充加号右边部分");
                }
            }
        }
        return node;
    }

    /**
     * 语法解析：乘法表达式
     * @return
     * @throws Exception
     */
    private SimpleASTNode multiplicative(TokenReader tokens) throws Exception {
        SimpleASTNode child1 = primary(tokens);
        SimpleASTNode node = child1;

        Token token = tokens.peek();
        if (child1 != null && token != null) {
            if (token.getType() == TokenType.Star || token.getType() == TokenType.Slash) {
                token = tokens.read();
                SimpleASTNode child2 = primary(tokens);
                if (child2 != null) {
                    node = new SimpleASTNode(ASTNodeType.Multiplicative, token.getText());
                    node.addChild(child1);
                    node.addChild(child2);
                } else {
                    throw new Exception("【加法表达式错误】：需要补充乘号右边部分");
                }
            }
        }
        return node;
    }

构建AST过程（递归）

    /**
     * 语法解析：根节点
     * @return
     * @throws Exception
     */
    private SimpleASTNode prog(TokenReader tokens) throws Exception {
        //构建根节点
        SimpleASTNode node = new SimpleASTNode(ASTNodeType.Programm, "Calculator");

        //构建子节点（递归完成）
        SimpleASTNode child = additive(tokens);

        if (child != null) {
            node.addChild(child);
        }
        return node;
    }

计算节点值（递归）

    /**
     * 对某个AST节点求值，并打印求值过程。
     * @param node
     * @param indent  打印输出时的缩进量，用tab控制
     * @return
     */
    private int evaluate(ASTNode node, String indent) {
        int result = 0;
        System.out.println(indent + "Calculating: " + node.getType());
        switch (node.getType()) {
            case Programm:
                for (ASTNode child : node.getChildren()) {
                    result = evaluate(child, indent + "\t");
                }
                break;
            case Additive:
                ASTNode child1 = node.getChildren().get(0);
                int value1 = evaluate(child1, indent + "\t");
                ASTNode child2 = node.getChildren().get(1);
                int value2 = evaluate(child2, indent + "\t");
                if (node.getText().equals("+")) {
                    result = value1 + value2;
                } else {
                    result = value1 - value2;
                }
                break;
            case Multiplicative:
                child1 = node.getChildren().get(0);
                value1 = evaluate(child1, indent + "\t");
                child2 = node.getChildren().get(1);
                value2 = evaluate(child2, indent + "\t");
                if (node.getText().equals("*")) {
                    result = value1 * value2;
                } else {
                    result = value1 / value2;
                }
                break;
            case IntLiteral:
                result = Integer.valueOf(node.getText()).intValue();
                break;
            default:
        }
        System.out.println(indent + "Result: " + result);
        return result;
    }

 输出

总结

• 递归下降算法中有“下降”和“递归”两个特点。它跟文法规则基本上是同构的，通过文法一定能写出算法。
• 左递归会导致递归进入死循环，因此递归需要从加法符号前后划分。
• 上下文无关文法比正则文法更具有普适性，区别在于前者可以递归嵌套，后者不能。

 完整代码：https://github.com/SongJain/TheBeautyOfCompiling/tree/master/SimpleCalculator

---

个人原创学习笔记，参考课程《编译原理之美》。