有限自动机字符串匹配

引言：

本文参考自《算法导论》中 “32.3 利用有限自动机进行字符串匹配” ，其目的不仅仅是为了改善常规算法的时间复杂度问题，更是为了给在解决类似情况提供一个有限自动机方案的参考。

很多字符串匹配算法都要建立一个有限自动机，它是一个处理信息的简单机器，通过对文本字符串 T 进行扫描，找出模式 P 的所有出现位置。这些字符串匹配的自动机都非常有效：它们只对每个文本字符检查一次，并且检查每个文本字符时所需的时间为常数。因此，在模式预处理完成并建立好自动机后进行匹配所需要的时间为 O(n) 。

1、朴素字符串匹配算法：

朴素字符串匹配算法时通过一个循环找到所有有效偏移，
该循环对 n-m+1 个可能的 s 进行检测，看是否满足条件 P[1…m] = T[s+1…s+m]。

朴素字符串匹配算法伪代码：

NAIVE-STRING-MATCHER(T,P)
    n=T.length
    m=P.length
    for s = 0 to n-m
        if p[1...m] == T[s+1,s+m]
            print "Pattern occurs with shift" s

最坏的情况下，朴素字符串匹配算法运行时间为 O((n-m+1)m)。

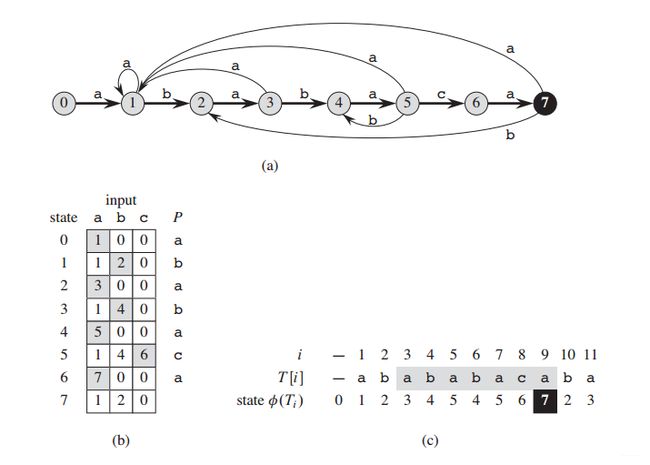
2、有限自动机：

一个有限自动机 M 是一个 5 元组（Q，q， A， ∑，δ）

Q 是状态的有限集合
q∈Q 是一个初始状态
A 包含于 Q 是一个特殊的接受状态集合
∑ 是有限输入字母表
δ 是一个从 Q✖∑ 到 Q 的函数，称为 M 的转移函数

下图为有限自动机的状态转移图，模式串为 ababaca 。

转移函数算法伪代码：

其中， Pk ⊇ Pqa 表示 Pk是 Pqa的后缀。

COMPUTE-TRANSITION-FUNCTION(P,∑)
    m = P.length
    for q = 0 to m
       for each charater a∈∑
          k = min(m+1,q+2)
          repeat
              k = k - 1
          until Pk ⊇ Pqa
          δ(q,a) = k
    return δ

有限自动机算法伪代码：

FINITE-AUTOMATON-MATCHER(T,δ,m)
    n = T.length
    q = 0
    for i = 1 to n
        q = δ(q,t[i])
        if q == m
            print "Pattern occurs with shift" i-m

3、详细代码：

转载自 https://blog.csdn.net/giftedpanda/article/details/86774815 。

#include
#include
#include
#include
#include

此外，有关字符串匹配的 KMP 算法，请参见：

https://blog.csdn.net/qq_30534935/article/details/100713917 。