锁相环讲解及simulink仿真
锁相环讲解及simulink仿真分析
- 一型锁相环
- 二型锁相环(电荷泵锁相环)
- 2.1 二型锁相环基本结构
- 2.2串联电阻锁相环结构
- 2.3.1二阶环路滤波器
- 2.3.2 三阶二型锁相环参数设计
- 三.锁相环simulink仿真
- 3.1三阶二型锁相环simulink建模
- 3.2 PFD的simulink建模
- 3.3 电荷泵simulink建模
- 3.4 环路滤波器设计及simulink仿真
- 3.5其余模块介绍省略
- 3.6整体仿真结果
- 总结
- 参考文献
本文基于对锁相环基本原理有一定了解的情况下讲述,不在分析锁相环的各类动态特性。锁相环基本知识可以参考拉扎维 模拟集成电路书第14 15章节。本文侧重于simulink仿真。
本文用到的参考文献以及simulink工程文件,点击此处下载
一型锁相环
一型锁相环由鉴相器 环路滤波器 压控振荡器组成。一型锁相环只鉴别相位
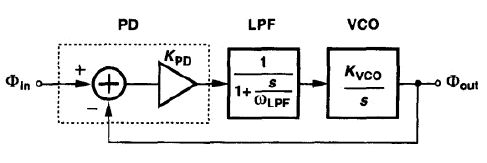
缺点:1. ξ ω n = 1 2 ω L P F \xi\omega_n=\frac 12\omega_{LPF} ξωn=21ωLPF,折衷关系
为了抑制低通滤波器输出电压的文波,滤波器的-3dB带宽必须小。由下式可知,当 ω n \omega_n ωn较小时,系统的稳定速度降低,锁定时间越长。
ω o u t ( t ) = [ 1 − 1 1 − ξ 2 e − ξ ω n t s i n ( 1 − ξ 2 + θ ) ] Δ ω u ( t ) \omega_{out}(t)={[ 1-\frac 1{\sqrt{1-{\xi^2}}}e^{-\xi\omega_nt}sin(\sqrt{1-\xi^2}+\theta) ]\Delta\omega u(t) } ωout(t)=[1−1−ξ21e−ξωntsin(1−ξ2+θ)]Δωu(t)
其中 θ = a r c s i n ( 1 − ξ 2 ) \theta=arcsin(\sqrt{1-\xi^2}) θ=arcsin(1−ξ2)
2.锁定范围有限(直接应用结论,没研究过。)
由于以上的两个缺点,一型锁相环不怎么用。下面研究二型锁相环。
二型锁相环(电荷泵锁相环)
.基本思路,为了提高锁定范围,先鉴频在鉴相,当 ∣ ω o u t − ω i n ∣ |\omega_{out}-\omega_{in}| ∣ωout−ωin∣足够小时,关闭鉴频,开启鉴相,直到锁定。
2.1 二型锁相环基本结构
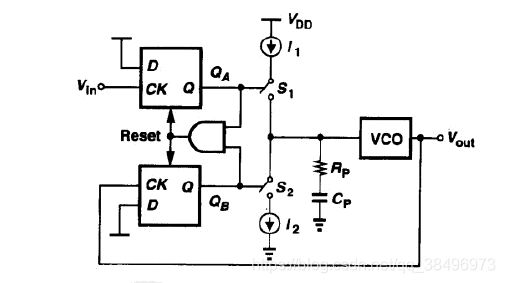
.下图所示为二型锁相环基本结构。理想情况下,如果存在相位/频率差,鉴频鉴相器输出脉冲信号,电荷泵就会对电容充电,时间足够长的话,电压无穷大。因为电容电压 V c o n t V_{cont} Vcont是一定的,不可能是无穷大,因此输入输出相位差理论上必须为零。这一点与一型锁相环不同。
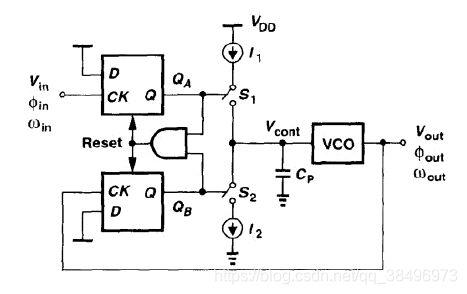
当 f b 与 f r e f 不 同 f_b与f_{ref}不同 fb与fref不同或者 ϕ b 和 ϕ r e f \phi_b和\phi_{ref} ϕb和ϕref不同时,UP( Q A Q_A QA)和DN( Q B Q_B QB)信号处出现不同宽度的脉冲信号。两者有短暂的重合部分,重合的时间大约为与门加复位的逻辑门延时。UP和DN信号控制开关S1 S2对电容 C P C_P CPc充放电,电容上的电压(UP和DN信号的平均值的差值)即为VCO的控制信号,调整输出频率。
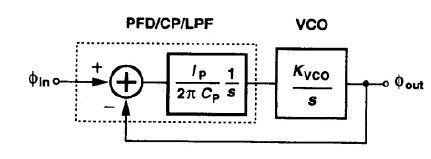
开环传递函数
ϕ o u t ϕ i n = I p 2 π C p K V C O s 2 \frac {\phi_{out}}{\phi_{in}}=\frac {I_p}{2\pi C_p} \frac {K_{VCO}}{s^2} ϕinϕout=2πCpIps2KVCO
闭环传递函数为:
H ( s ) = I P K V O C 2 π C P s 2 + I P K V C O 2 π C P H(s)=\frac {\frac {I_P K_{VOC}}{2\pi C_P}}{s^2+\frac {I_PK_{VCO}}{2\pi C_P}} H(s)=s2+2πCPIPKVCO2πCPIPKVOC
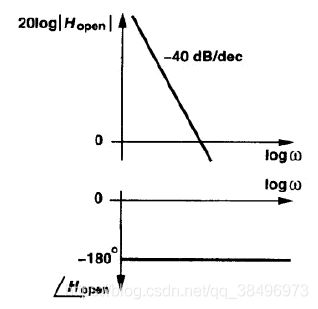
由于反馈系数为1,开环传递函数即为环路增益,其在原点处有2个极点,相移 18 0 0 180^0 1800, 称为二型锁相环。
如图2.3所示,环路频率特性不稳定。为了使得环路稳定,通常引入零点即串联电阻R。
本文用到的参考文献以及simulink工程文件,点击此处下载
2.2串联电阻锁相环结构
根据2.1节的分析,可知,为了稳定环路,需要增加电阻R,引入零点。增加相位裕度。
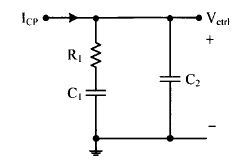
电路结构如图2.4所示:
2.3.1二阶环路滤波器
Z 2 n d = 1 s C 2 / / ( R 1 + 1 s C 1 ) = 1 + s T 1 S ( C 1 + C 2 ) ( 1 + s T 2 ) (1) Z_{2nd}= \frac 1{sC_2}//(R_1+\frac 1{sC_1})= \frac {1+sT_1}{S(C_1+C_2)(1+sT_2)} \tag{1} Z2nd=sC21//(R1+sC11)=S(C1+C2)(1+sT2)1+sT1(1)
其中: T 1 = R 1 C 1 , T 2 = R 1 C 1 C 2 C 1 + C 2 T_1=R_1C_1 ,T_2=\frac {R_1C_1C_2}{C_1+C_2} T1=R1C1,T2=C1+C2R1C1C2
2.3.2 三阶二型锁相环参数设计
利用2.3.1节中的*式,加入VCO的积分特性可得锁相环的开环传递函数(即环路增益)为
H o l ( s ) = I C P K V C O 2 π 1 + s T 1 s 2 ( C 1 + C 2 ) ( 1 + s T 2 ) (2) H_{ol}(s)=\frac {I_{CP}K_{VCO}}{2\pi} \frac {1+sT_1}{s^2(C_1+C_2)(1+sT_2)} \tag{2} Hol(s)=2πICPKVCOs2(C1+C2)(1+sT2)1+sT1(2)

求解相位裕度: P M = a r c t a n ( ω T 1 ) − a r c t a n ( ω T 2 ) (3) PM=arctan(\omega T_1)-arctan(\omega T_2 \tag{3}) PM=arctan(ωT1)−arctan(ωT2)(3)
上式对频率求导数,并令求导结果为0,得到相位裕度最大的时候,满足以下关系:
ω c = 1 T 1 T 2 (4) \omega_c=\frac 1{\sqrt{T_1T_2}} \tag{4} ωc=T1T21(4)
令开环传递函数(环路增益)的模为1,结合上式求得环路带宽:
ω c = I C P K V C O R 1 2 π C 1 C 1 + C 2 (5) \omega_c=\frac {I_{CP}K_{VCO}R_1}{2\pi} \frac {C_1}{C_1+C_2} \tag{5} ωc=2πICPKVCOR1C1+C2C1(5)
利用PM表达式和 ω c = 1 T 1 T 2 \omega_c=\frac 1{\sqrt{T_1T_2}} ωc=T1T21求解 T 1 T 2 T_1T_2 T1T2,求解过程利用了 a r c t a n ( x ) + a r c t a n ( 1 / x ) = π / 2 arctan(x)+arctan(1/x)=\pi/2 arctan(x)+arctan(1/x)=π/2
解得:
T 1 = t a n P M + π / 2 2 ω c (6) T_1=\frac {tan\frac {PM+\pi/2}2 }{\omega_c} \tag{6} T1=ωctan2PM+π/2(6)
T 2 = 1 ω c t a n ( 90 + P M ) 2 (7) T_2=\frac 1{\omega_ctan\frac {(90+PM)}2} \tag{7} T2=ωctan2(90+PM)1(7)
根据5 6 7三式求解电容电阻值。
R 1 = ω c / [ I C P K V C O 2 π ( 1 − T 2 / T 1 ) ] (8) R_1=\omega_c/[\frac {I_{CP}K_{VCO}}{2\pi}(1-T_2/T_1)] \tag{8} R1=ωc/[2πICPKVCO(1−T2/T1)](8)
C 1 = T 1 R 1 (9) C_1=\frac {T_1}{R_1}\tag{9} C1=R1T1(9)
C 2 = C 1 / ( T 1 T 2 − 1 ) (10) C_2=C_1/(\frac {T_1}{T_2}-1)\tag{10} C2=C1/(T2T1−1)(10)
注意这里的8 9 10三个式子,后面设计环路滤波器的时候经常使用
三.锁相环simulink仿真
本文用到的参考文献以及simulink工程文件,点击此处下载
3.1三阶二型锁相环simulink建模
所谓三阶二型锁相环:采用2.3节的二阶滤波器,由于VCO相当于积分器,传递函数为 K V C O s \frac {KVCO}s sKVCO。系统整体的传递函数变为三阶。
参考时钟 F C L K = 30 M H z F_{CLK}=30MHz FCLK=30MHz 环路带宽 f c = 800 K H z f_c=800KHz fc=800KHz,电荷泵充放电电流 I C P = 20 u A I_{CP}=20uA ICP=20uA 压控振荡器调谐增益 K V C O = 30 M H z / V K_{VCO}=30MHz/V KVCO=30MHz/V
下面分模块详细介绍设计过程。
3.2 PFD的simulink建模
1.UP和DN信号经过与非门后反馈到复位端,要人为的加入延时模块,Tranaport delay ,由于transport delay和logic operator数据类型冲突,加入data type convesion模块进行数据转换。
2.不用的端口不能悬空,用terminator模块连接
3.3 电荷泵simulink建模
电荷泵本质是压控电流源,在UP和DN信号控制下,控制电流输出,当UP=1时,恒定电流输出,UP=0时,无电流输出。DN信号同理,只是电流方向相反。
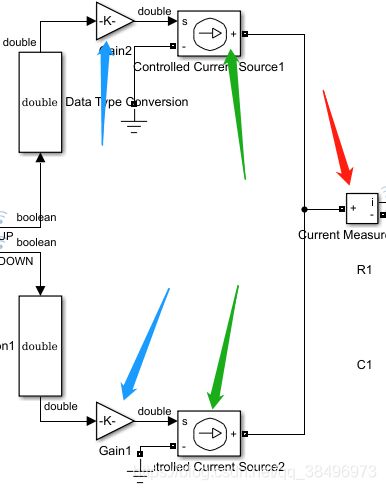
1.PFD输出信号是boolean类型,Gain模块输入是double类型,需要数据转换模块。
2.电荷泵输出电流大小通过增益模块gain控制,此处**Gain2=20uA, Gain1=-20uA**
3.将gain模块输出的double信号通过contrlled current source转换为电流信号。
4.由于后级的滤波器网络属于电气接口,加入current measurement模块做信号转换。
3.4 环路滤波器设计及simulink仿真
为了叙述方便,再次重申系统要求,下面根据系统的性能要求设计RC参数。
参考时钟 F C L K = 30 M H z F_{CLK}=30MHz FCLK=30MHz 环路带宽 f c = 800 K H z f_c=800KHz fc=800KHz,电荷泵充放电电流 I C P = 20 u A I_{CP}=20uA ICP=20uA 压控振荡器调谐增益 K V C O = 30 M H z / V K_{VCO}=30MHz/V KVCO=30MHz/V
根据2.3.2节中式5-10可以计算出环路滤波器的参数。这里采用matlab编程求解。
一般情况下,环路带宽约为参考频率的0.1倍,这里取800KHz
PM=50/180*pi;
I=20*10^-6;
fc=800000;
KVCO=30*10^6;
wc=2*pi*fc;
T1=(sec(PM)+tan(PM))/wc;
T2=(sec(PM)-tan(PM))/wc;
R1=wc/(I*KVCO*(1-T2/T1));
C1=T1/R1;
C2=C1/(T1/T2-1);
求解结果: C 1 = 56.6 p f , C 2 = 8.6 p f , R 1 = 9.65 K C_1=56.6pf,C_2=8.6pf,R_1=9.65K C1=56.6pf,C2=8.6pf,R1=9.65K
可以单独仿真锁相环的额开环传递函数,确保环路带宽和相位裕度满足要求。环路频率响应分析请点击此处连接
本文用到的参考文献以及simulink工程文件,点击此处下载
3.5其余模块介绍省略
3.6整体仿真结果
总结
根据本次仿真,根据自己系统的需要,先搭建simulink仿真电路,利用环路频率响应分析请点击此处连接利用线性分析工具,仿真锁相环传递函数,分析其相位裕度,环路带宽等频率特性。最后整体仿真。
注意各个模块之间的数据类型,和信号接口。
参考文献
本文的一些电路结构及公式计算参考如下:
宽带CMOS分数频率合成器的研究与实现——黄福青,博士论文
基于Matlab/Simulink的频率合成器模型设计——郝连秀
本文用到的参考文献以及simulink工程文件,点击此处下载