GPUImage的图像形变设计(复杂形变部分)
在上一部分,我们介绍了两种简单形变的GPUImage实现方式,包括自定义FragmentShader,和自定义顶点数组。这一部分,我们将介绍更为复杂的一些图像形变的实现。
Part3:基于自定义vertices的局部图像形变设计
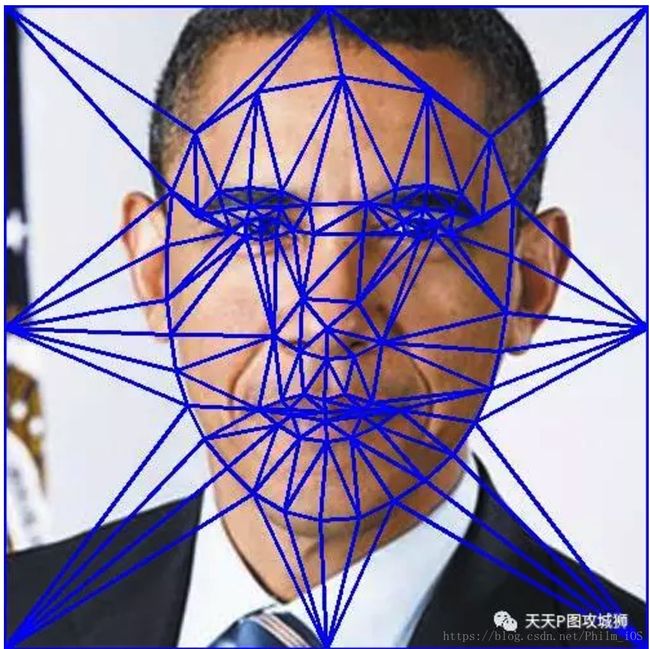
区别于Part2中的自定义vertices和fragment数组的简单图像形变,这里的自定义vertices数组不仅仅局限于图像4个顶点,而是可以任意指定的,从而可以达到对图像的局部区域进行细微的形变调整。这里,我们以调整用户的脸型,从而达到蛇精脸的效果为例,如下图所示:

对于用户图像的人脸区域,我们分隔成若干个三角形切片,然后通过调节这些三角形的顶点来实现形变。具体的做法是:
1) 得到原始三角形顶点位置(原始特征点,图中红色点)
2) 得到需要形变后的三角形顶点位置(形变特征点,图中蓝色点)
3) 通过设置vertices和textureCoordinates来调整三角形(vertices对应新地形变后特征点,textureCoordinates对应原图的原始特征点)
4) 通过OpenGL绘制相应的三角形,即得到形变后的图像
这里需要单独设置的内容相比简单形变要复杂一些,需要同时设置多组vertices和textureCoordinates,并且在绘制三角形时也应该绘制GL_TRIANGLES而非GL_TRIANGLE_STRIP,这是因为很难得到连续顶点的三角形数组。具体代码如下:
这里mVertex和mFragment都是nTriangles*3*2个值(nTriangle个三角形,每个三角形3个顶点,每个顶点2个float值)
另外需要注意的是三角形划分,必须保证一个固定不变的区域内所有面积都要有所覆盖,否则会形成空洞(对于上图的例子,需要在最外围设置一个正方形,保持正方形的4条边不动的情况下,调整正方形区域内的顶点,从而可以达到形变后的图像任然连续这一个结果)。
如上图所示,需要外框点保持不变,通过调节内部的0~98号点(内部点),来实现形变后的图像与原图保持连续。
Part4:基于网格形变的自定义vertices全局图像形变设计
对于Part3中的自定义顶点的方法来实现图像形变而言,需要确定三角形的具体分割,并且仅支持线性的位置调整,对于非线性的位置调整(比如大眼,越离眼睛中心形变越大)则支持能力较弱,这时候就需要使用这里的基于网格形变的自定义vertices全局图像形变方法来进行图像形变了。
这种方法的本质思想是:对于图片上的每一个像素,手动计算出该像素在新的图片中的位置,并且将该像素值填充至该位置。然而,单独计算每一个像素点的位置需要大量的计算资源,无法达到实时处理的性能,为此,通过对图片进行分块,每一块都是一个小三角形。通过对小三角形顶点的位置调整,来大致近似每一个点的位置移动,从而便于OpenGL进行渲染。具体的分块示意图如下所示:
从上图可以看出,当分块足够多时,变相相当于逐像素计算新的位置;而当位置足够少时(比如只有1*1的顶点),则退化为普通的顶点坐标变换。
那么,具体应该如何计算每一个点在新图像中的位置呢?这里给出常用的2种方法:
1) MLS方法:利用论文《Image Deformation Using Moving Least Squares》中的方法,当已知某些点在新图中的新位置之后(锚定点),对于每个像素点,可以依据该像素点与锚定点之间的关系,计算得到该像素点在新图像中的位置,从而达到形变的目的。下图是MLS算法的一个示例:
2) 基于规则的点位置计算:也是最传统的点计算方法。该方法通过设定一些具体的规则(比如,某个像素A的邻域内点往方向v移动x个像素,则对于任意一个像素点,判断它与A之间的关系,如果落在A的邻域内,则往v方向移动x个像素)。这些规则可以很简单(移动、扩大、收缩),也可以很复杂(按指定路径移动,非线性移动),从而可以组合出各种效果。比如Part3中的瘦脸,也可以对脸部轮廓的像素进行移动来实现近似的效果。具体的效果如下图所示,左边是原图,右边是每个网格点移动后形变产生的图片。

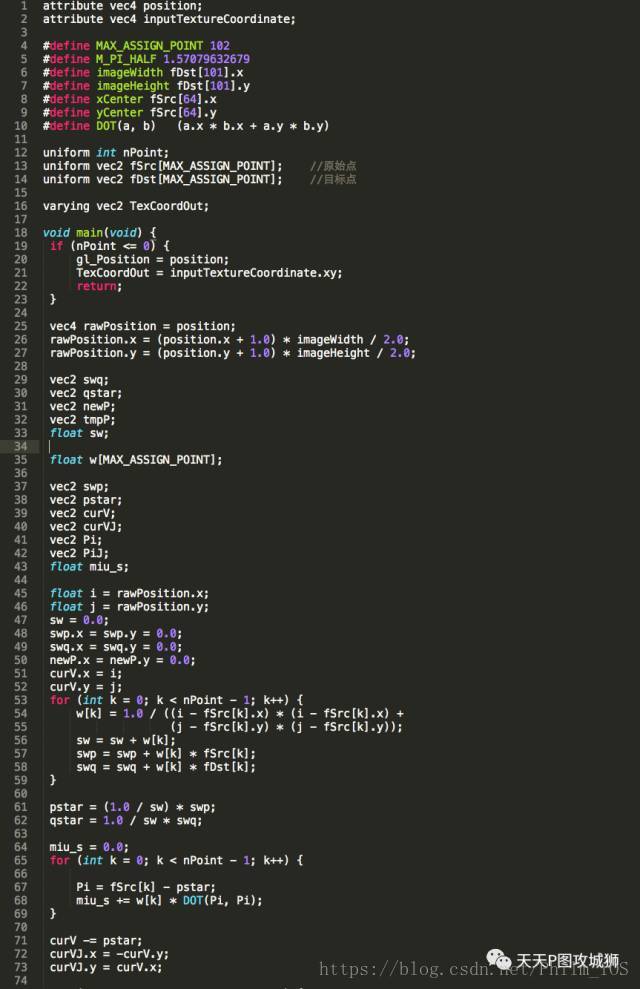
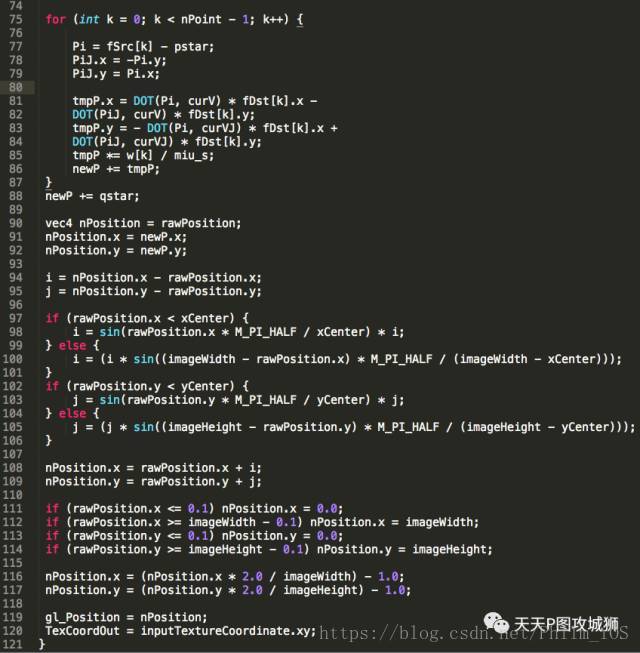
上面两种是比较常用的点移动方法。对于点位置的计算,可以放在CPU端进行,再将计算结果赋值给vertices数组,也可以直接传默认的vertices数组,将点位置的计算交给GPU来做。如果通过GPU来计算点的位置,可以获得GPU的并行加速能力,缺点是需要传输额外的数据给GPU(MLS算法需要传点的映射关系;规则方法需要传规则本身),因此各有优缺点。这里举例通过GPU来计算MLS算法中的点位置的变化:
小结:
GPUImage提供了很方便的接口供我们来对图像进行形变的操作。对于简单的形变,可以通过自定义vertices数组来实现,也可以通过改写FragmentShader来实现;对于复杂的形变,可以同时自定义vertices和textureCoordinates数组来通过自定义贴三角形的方式来实现,也可以通过将图像分割成网格状,再绘制每一个小三角形的方式来实现。
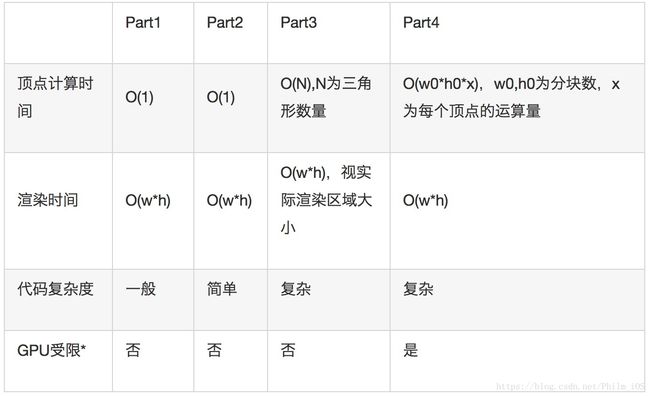
下面是各种方式的时间复杂度以及代码复杂度:(假设图像宽度w,高度h)