2021秋招-leetcode刷题-未分类
leetcode刷题-不知道怎么分类的
每日一题: leetcode-面试题 16.18. 模式匹配-中等(2020-06-22)
面试题 16.18. 模式匹配
大佬题解-针对pattern形式分类讨论
面试题 16.18. 模式匹配
你有两个字符串,即pattern和value。 pattern字符串由字母"a"和"b"组成,用于描述字符串中的模式。
例如,字符串"catcatgocatgo"匹配模式"aabab"(其中"cat"是"a","go"是"b"),
该字符串也匹配像"a"、"ab"和"b"这样的模式。但需注意"a"和"b"不能同时表示相同的字符串。
编写一个方法判断value字符串是否匹配pattern字符串。
示例 1:
输入: pattern = "abba", value = "dogcatcatdog"
输出: true
示例 2:
输入: pattern = "abba", value = "dogcatcatfish"
输出: false
示例 3:
输入: pattern = "aaaa", value = "dogcatcatdog"
输出: false
示例 4:
输入: pattern = "abba", value = "dogdogdogdog"
输出: true
解释: "a"="dogdog",b="",反之也符合规则
思路
思路
简单说就是统计a和b的数量,比如统计到3个a和2个b。
然后就是解方程:3 * str_a.length() + 2 * str_b.length() = value.length()
其中:str_a是指代表a的字符串,str_b是指代表b的字符串,value是指patternMatching(String pattern, String value)方法的第2个参数。
至于怎么解呢?穷举就完事了。
需要注意的是,str_a或str_b可以为空字符串"",同时题目要求:str_a不能与str_b相同。
class Solution:
def patternMatching(self, pattern: str, value: str) -> bool:
'''
时间复杂度分析: 两层for循环,最差情形: O(MN)
空间复杂度分析: set_a , set_b , O(M)
'''
# 思路: 本质 解方程: pattern_a_count * pattern_a_len + pattern_b_count * pattern_b_len = value_len
# pattern_a: 1) 字符串; 2) 空 pattern_a 和 pattern_b 不同
# 如何解? 分情况讨论,穷举
# case1: pattern和value都为空,返回True; 0*0 + 0*0 = 0
if not value and not pattern:
return True
# case2: pattern 为空, 0*0 + 0*0 != value_len, 仅pattern为空: 返回False
if not pattern:
return False
# case3: value为空, value_len = 0,
# 仅value为空,这时候分两种情况:
# 如果pattern中只存在a或者b一种,那么令a或者b为空,符合条件,返回True;
# 否则,由于不同pattern不能表示同一字符串,返回False
if not value:
if len(pattern) == 1:
return True
else:
return False
# case4: 模式串中只有一种字符 pattern_a_count = 0 or pattern_b_count = 0 1) 模式串长度区分;
# 都不为空的情况下:如果pattern中只有a或者b一种,那意味这value全由一种字符串构成。
# 它需满足以下两个条件:
# 首先,value的长度需要被pattern的长度整除;
# 其次,value中的每一个字符串需要都是a,根据value长度和pattern长度很容易计算出a的长度,然后顺次取出看是否相同即可。
if len(set(pattern)) == 1:
if len(value) % len(pattern) != 0:
return False
sub_string_length = len(value) // len(pattern)
# []内元素 为 0,'',False --> 返回False, []为空,或者不存在上述返回 True;
return all([value[i:i+sub_string_length] == value[0:sub_string_length] for i in range(0, len(value), sub_string_length)])
# case5: count_a =1 or count_b =1 另另一个 count = 0即可; 如果pattern中同时含有a和b,也有两种情况。
# 第一种,其中一个pattern只有一个,假设a只有一个,那么只需要令a= value, b=“”,即可,所以直接返回True
if pattern.count('a') == 1 or pattern.count('b') == 1:
return True
# case6: 另一种情况,同时含有a, b且个数都大于1。
# 这时候,我们先统计pattern中a, b各有多少个,然后遍历a的所有可能长度,对于某个确定的a的长度,
# 结合a的个数和b的个数以及value的长度,我们即可以确定b的长度。
# 这时候需要满足以下条件:1) 首先b的长度也必须是整数; 2) 其次,value只能由a, b结合而成。
cnt_a = pattern.count('a')
cnt_b = pattern.count('b')
for i in range(len(value) // cnt_a): # 遍历a所有的长度
remain_length = len(value) - i * cnt_a
# 如果长度不满足首先排除
if remain_length % cnt_b != 0:
continue
# pattern_b 对应的字符string长度
j = remain_length // cnt_b
set_a = set()
set_b = set()
p = 0
for s in pattern:
if s == 'a':
set_a.add(value[p:p+i]) # 将 value[p:p+i] 一个 a 模式加入set_a
p += i
if s == 'b':
set_b.add(value[p:p+j])
p += j
if len(set_a) == len(set_b) == 1:
return True
# 找不到满足条件 a 长度
return False
LRU算法
LRU算法详解
leetcode-146. LRU缓存机制-中等
二、LRU 算法描述
LRU 算法实际上是让你设计数据结构:首先要接收一个 capacity 参数作为缓存的最大容量,然后实现两个 API,一个是 put(key, val) 方法存入键值对,另一个是 get(key) 方法获取 key 对应的 val,如果 key 不存在则返回 -1。
注意哦,get 和 put 方法必须都是 O(1) 的时间复杂度,我们举个具体例子来看看 LRU 算法怎么工作。
/* 缓存容量为 2 */
LRUCache cache = new LRUCache(2);
// 你可以把 cache 理解成一个队列
// 假设左边是队头,右边是队尾
// 最近使用的排在队头,久未使用的排在队尾
// 圆括号表示键值对 (key, val)
cache.put(1, 1);
// cache = [(1, 1)]
cache.put(2, 2);
// cache = [(2, 2), (1, 1)]
cache.get(1); // 返回 1
// cache = [(1, 1), (2, 2)]
// 解释:因为最近访问了键 1,所以提前至队头
// 返回键 1 对应的值 1
cache.put(3, 3);
// cache = [(3, 3), (1, 1)]
// 解释:缓存容量已满,需要删除内容空出位置
// 优先删除久未使用的数据,也就是队尾的数据
// 然后把新的数据插入队头
cache.get(2); // 返回 -1 (未找到)
// cache = [(3, 3), (1, 1)]
// 解释:cache 中不存在键为 2 的数据
cache.put(1, 4);
// cache = [(1, 4), (3, 3)]
// 解释:键 1 已存在,把原始值 1 覆盖为 4
// 不要忘了也要将键值对提前到队头
三、LRU 算法设计
分析上面的操作过程,要让 put 和 get 方法的时间复杂度为 O(1),我们可以总结出 cache 这个数据结构必要的条件:查找快,插入快,删除快,有顺序之分。
因为显然 cache 必须有顺序之分,以区分最近使用的和久未使用的数据;而且我们要在 cache 中查找键是否已存在;如果容量满了要删除最后一个数据;每次访问还要把数据插入到队头。
那么,什么数据结构同时符合上述条件呢?哈希表查找快,但是数据无固定顺序;链表有顺序之分,插入删除快,但是查找慢。所以结合一下,形成一种新的数据结构:哈希链表。
LRU 缓存算法的核心数据结构就是哈希链表,双向链表和哈希表的结合体。这个数据结构长这样:
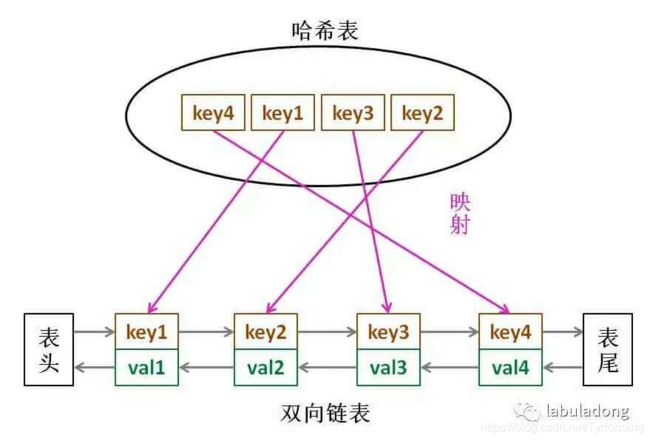
思想很简单,就是借助哈希表赋予了链表快速查找的特性嘛:可以快速查找某个 key 是否存在缓存(链表)中,同时可以快速删除、添加节点。回想刚才的例子,这种数据结构是不是完美解决了 LRU 缓存的需求?
也许读者会问,为什么要是双向链表,单链表行不行?另外,既然哈希表中已经存了 key,为什么链表中还要存键值对呢,只存值不就行了? (也是我的问题)
想的时候都是问题,只有做的时候才有答案。 这样设计的原因,必须等我们亲自实现 LRU 算法之后才能理解,所以我们开始看代码吧~
四、代码实现
首先,我们把双链表的节点类写出来,为了简化,key 和 val 都认为是 int 类型:
# 看不懂。。。。
class Node {
public int key, val;
public Node next, prev;
public Node(int k, int v) {
this.key = k;
this.val = v;
}
}
然后依靠我们的 Node 类型构建一个双链表,实现几个需要的 API(这些操作的时间复杂度均为 O(1)):
class DobuleList():
# 在链表头部添加节点x,时间为O(1);
def addFirst(Node x):
pass
# 删除链表中的 x 节点(x 一定存在)
# 由于是双链表且给的目标是 Node节点, 时间: O(1)
def remove(Node x):
pass
# 删除链表中最后一个节点,并返回该节点,时间:O(1)
def removeLast():
pass
# 返回链表长度, 时间: O(1)
def size():
pass
PS:这就是普通双向链表的实现,为了让读者集中精力理解 LRU 算法的逻辑,就省略链表的具体代码。
为什么必须要用双向链表?
回答: 因为要进行删除操作。 删除一个节点不光要得到该节点本身的指针,也需要操作其前驱节点的指针,而双向链表才能支持直接查找前驱,保证操作的时间复杂度为: O(1)。
有了双向链表的表现,我们只需要在LRU算法中把它和哈希表结合起来即可。 逻辑:
# key 映射到Node(key, val)
def map():
pass
# Node(k1, v1) <--> Node(k2, v2)...
DoubleList cache
def get(key):
if key 不存在:
return -1
else:
将数据(key, val) 提到开头。
return val
def put(key, val):
Node x = new Node(key, val)
if key 已存在:
把旧数据删除;
将心节点X插入到开头。
else:
if cache 已满:
删除链表的最后一个位置腾数据。
删除 map 中映射到 该数据的键。
将新节点 x 插入到开头
map 中新建 key 对 新节点 x 的映射
进一步翻成代码
class LRUCache():
# key -> Node(key, val)
MAP
# Node(k1, v1) <-> Node(k2, v2)
DoubleList cache
# 最大容量
cap
def get(key):
if key not in map:
return -1
val = map.get(key).val
# 利用 put方法把该数据提前
put(key, val)
return val
def put(key, val):
# 先把新节点X做出来
Node x = Node(key, val)
# key如果已经存在
if key in map:
# 删除旧的节点, 新的插到头部
cache.remove(map.get(key))
cache.addFirst(x)
# 更新 map 中对应的数据
map.put(key, x)
else:
# 如cache已经满了
if cap == len(cache):
# 删除链表最后一个数据
Node last = cache.removeLast()
map.remove(last.key)
# 直接添加到头部
cache.addFirst(x)
map.put(key, x)
问题: 为什么要在链表中同时存储 key 和 val , 而不只是存储 val ?
if cap == len(cache):
# 删除链表最后一个数据
Node last = cache.removeLast()
map.remove(last.key)
回答: 当缓存容量已满,我们不仅仅要删除最后一个Node节点,还要把 map 中映射到 该节点的 key 同时删除, 而这个 key 只能由 Node 得到。 如果 Node 结构只存储val, 那我们就无法得知 key 是什么, 就无法删除 map 中的键,造成错误。
注意 :
容易犯错的一点是:处理链表节点的同时不要忘了更新哈希表中对节点的映射。
python 代码完整版本:
class ListNode():
'''
双向链表单个节点数据结构的实现, 不用考虑hasmap到节点的映射;
'''
def __init__(self, key=None, value= None):
self.key = key
self.val = value
self.prev = None
self.next = None
自己画图:

本质: hasmap{} 中存储: key: Node(key, val) 以代表 字典到链表的映射,至于具体怎样实现不用管,假设已经可以直接实现字典找到一个Node(key, val) 可以直接在 链表中找到,也就是 字典到链表映射自动完成 。
这个代码是将: move_node_to_tail 单独写出来了,方便操作,上面的思路也可以套用。 不方便理解。
class LRUCache:
# 初始化操作
def __init__(self, capacity: int):
self.capacity = capacity
self.hasMap = {}
# 新建两个ListNode节点;
# head: 头部节点, 久未使用
# tail: 尾部节点, 最近使用(访问、插入)
self.head = ListNode()
self.tail = ListNode()
# 初始化双向链表
self.head.next = self.tail
self.tail.prev = self.head
# 因为get 与 put 操作都可能需要将双链表中的某个节点移动到 末尾, 所以单独定义一个方法
def move_node_to_tail(self, key):
# 先将哈希表key指向的节点拎出来,为了简洁起名 node
# hasmap[key] hasmap[key]
# | --> |
# prev <-> node <->next prev <-> next .... node
node = self.hasMap.get(key) # self.getMap[key]
# 删除当前节点
node.prev.next = node.next
node.next.prev = node.prev
# 然后将node节点插入 尾节点前面
node.prev = self.tail.prev
node.next = self.tail
self.tail.prev.next = node
self.tail.prev = node
def get(self, key: int) -> int:
# 情况1: 如果不在hasMap中, 返回 -1
# 情况2: 该节点变为最近使用,移动到 tail, 并返回 val
if key not in self.hasMap:
return -1
self.move_node_to_tail(key)
val = self.hasMap.get(key).val
return val
def put(self, key: int, val: int) -> None:
# 情况1: key 已经在 hasMap中(Node 在链表中), 则不需要链表加入新节点,更新val, 并移动到末尾;
if key in self.hasMap:
# 注意: 链表和字典是可以当作一起的, 直接更新 字典中Node.val 相当于 链表Node同步更新
self.hasMap[key].val = val
self.move_node_to_tail(key)
# 情况2: key不在hasMap 中;
# 情况2.1: cache缓存已经满, 删除尾部很久未访问节点(head), 并删除hasMap中对应key值;
# 这块感觉不是很合理呀, 为什么两个不能同时删除
# 情况2.2: cache 没满
else:
if len(self.hasMap) == self.capacity:
# hasMap 进行key 值删除
self.hasMap.pop(self.head.next.key)
# 双链表删除: 很久未访问节点, 即: 头节点的 next节点;
self.head.next = self.head.next.next
self.head.next.prev = self.head
# 如果容量足够
newNode = ListNode(key, val)
self.hasMap[key] = newNode
newNode.prev = self.tail.prev
newNode.next = self.tail
self.tail.prev.next = newNode
self.tail.prev = newNode
Trie字典树
Trie字典树原理-详解
poecai大佬-前缀树系列
208. 实现 Trie (前缀树)
难度
中等
346
实现一个 Trie (前缀树),包含 insert, search, 和 startsWith 这三个操作。
示例:
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 true
trie.search("app"); // 返回 false
trie.startsWith("app"); // 返回 true
trie.insert("app");
trie.search("app"); // 返回 true
python实现:
class Trie:
def __init_(self):
'''
Initializer your data structure here
'''
# 使用最简单字典实现;
self.lookup = {}
def insert(self, word:str):
'''
Inserts a word into the trie.
'''
tree = self.lookup
for w in word:
if w not in tree:
tree[w] = {}
tree = tree[w]
# 单词结束标志: {t:{o:{#:#}}}
tree['#'] = '#'
def search(self, word:str):
'''
Returns if the word is in the trie
必须搜索到叶子节点,中间节点存在不算
'''
tree = self.lookup
for w in word:
if w not in tree:
return False
tree = tree[w]
if '#' in tree:
return True
return False
def startsWith(self, prefix:str):
'''
Returns if there is any word in the trie that starts with the given prefix
'''
tree = self.lookup
for w in prefix:
if w not in tree:
return False
tree = tree[w]
return True
class Trie:
def __init__(self):
"""
Initialize your data structure here.
"""
self.lookup = {}
def insert(self, word: str) -> None:
"""
Inserts a word into the trie.
"""
tree = self.lookup
for a in word:
if a not in tree:
tree[a] = {}
tree = tree[a]
# 单词结束标志
tree["#"] = "#"
def search(self, word: str) -> bool:
"""
Returns if the word is in the trie.
"""
tree = self.lookup
for a in word:
if a not in tree:
return False
tree = tree[a]
if "#" in tree:
return True
return False
def startsWith(self, prefix: str) -> bool:
"""
Returns if there is any word in the trie that starts with the given prefix.
"""
tree = self.lookup
for a in prefix:
if a not in tree:
return False
tree = tree[a]
return True
leetcode-208. 实现 Trie (前缀树)-中等
leetcode-211. 添加与搜索单词-中等
leetcode-212. 单词搜索 II-困难
leetcode-421. 数组中两个数的最大异或值-中等
并查集(Union-Find)
教程
labuladong-Union-Find 并查集算法详解
labuladong-Union-Find 算法怎么应用?
⭐liweiwei大佬-并查集总结使用并查集处理不相交集合问题(Java、Python)
刷题
leetocode-130. 被围绕的区域-中等
leetcode-990. 等式方程的可满足性-中等-AC
liweiwei大佬-并查集总结使用并查集处理不相交集合问题(Java、Python)
解题思路:
由于等式相等具有传递性,比较容易想到使用并查集。
为此设计算法如下:
1. 扫描所有等式, 将等式两边的顶点进行合并。
2. 再扫描所有的不等式, **检查** 每一个不等式的两个顶点是不是在一个联通分量里, 如果在: 则返回False, 表示方程式 有矛盾。
如果所有检查都没有矛盾,返回True。
并查集知识小结:
1.解决的是两个顶点是否联通的问题,可以用于检测图中是否存在环。
2.代表元法:采用 parent 数组实现,以每个节点的根节点作为代表元。
3.并查集有2种优化策略:
3.1 路径压缩: 隔代压缩、完全压缩
a) 【隔代压缩】: 性能比较高,虽然压缩不完全,不过多次执行【 隔代压缩】 也能达到 【完全压缩】 的效果, 推荐 隔代压缩
b) 【完全压缩】:需要借助系统栈, 使用递归的写法。 或者先找到当前节点的根节点,然后把沿途上所有的节点都指向根节点, 得遍历两次。
秩也有两种含义:
a) 秩表示以当前节点 为根节点的子树节点总数, 即这里的 秩 表示 size 含义;
b) 秩表示以当前节点为根节点的子树的高度,即这里的 秩 表示 rank 含义(更合理,因为查询时候的时间性能主要决定于树的高度)。
- 如果同时使用 路径压缩 和 按秩合并, 这里的 【秩】就失去了它的定义,但是即使 秩 表示的含义不准确,也能够作为合并时候很好的参考。 在这种情况下,并查集的查询和合并的时间复杂度都可以接近 O(1)。
策略是这样的(仅供参考):用「隔代压缩」,代码比较好写。不写「按秩合并」,除非题目有一些关于「秩」的信息需要讨论。一般来说,这样写也能得到不错的性能,如果性能不太好的话,再考虑「按秩合并」。
liweiwei 大佬参考: ord() 计算 字符 asicc码
class UnionFind:
def __init__(self, n):
# 此处: 由于只涉及26个字母,所以直接使用0-25替代
self.parent = [i for i in range(n)] # [0, 1, 2......25]
def find(self, x):
# 自己是否对应自己的父节点, 下标以及本身元素是对应的
while x != self.parent[x]:
# 隔代路径压缩
self.parent[x] = self.parent[self.parent[x]]
x = self.parent[x]
return x
def union(self, x, y):
root_x = self.find(x)
root_y = self.find(y)
# 这里未使用 秩 压缩
self.parent[root_x] = root_y
def is_connected(self, x, y):
return self.find(x) == self.find(y)
class Solution:
def equationsPossible(self, equations: List[str]) -> bool:
unionFind = UnionFind(26)
for equation in equations:
if equation[1] == '=':
index1 = ord(equation[0]) - ord('a')
index2 = ord(equation[3]) - ord('a')
unionFind.union(index1, index2)
for equation in equations:
if equation[1] == '!':
index1 = ord(equation[0]) - ord('a')
index2 = ord(equation[3]) - ord('a')
if (unionFind.is_connected(index1, index2)):
return False
return True
if __name__ == '__main__':
solution = Solution()
equations = ["c==c", "b==d", "x!=z"]
res = solution.equationsPossible(equations)
print(res)
union之前:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25]
union之后:[1, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25]
leetcode-547. 朋友圈-中等
547. 朋友圈
班上有 N 名学生。其中有些人是朋友,有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友,
B 是 C 的朋友,那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈,是指所有朋友的集合。
给定一个 N * N 的矩阵 M,表示班级中学生之间的朋友关系。如果M[i][j] = 1,表示已知第 i 个和 j 个学生互为朋友关系,
否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
示例 1:
输入:
[[1,1,0],
[1,1,0],
[0,0,1]]
输出: 2
说明:已知学生0和学生1互为朋友,他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回2。
大佬代码-直接复制,还未自己写:
class Solution():
def __init__(self):
"""
初始化变量
"""
self.tree_num = 0 # 连通集个数
self.tree_node = [] # 根节点所在树的节点总数,被合并的停止更新
self.parent = [] # 每个节点的父亲节点
def initialize_tree(self, total_node):
"""
初始化所有节点树
"""
self.tree_num = total_node
self.tree_node = [1] * total_node
self.parent = [i for i in range(total_node)]
def union(self, node_i, node_j):
"""
归并i和j树
"""
root_i = self.find(node_i)
root_j = self.find(node_j)
if root_i == root_j:
return
if self.tree_node[root_i] > self.tree_node[root_j]:
self.parent[root_j] = root_i
self.tree_node[root_i] += self.tree_node[root_j]
else:
self.parent[root_i] = root_j
self.tree_node[root_j] += self.tree_node[root_i]
self.tree_num -= 1
def find(self, node):
"""
查找节点的根
"""
while self.parent[node] != node:
self.parent[node] == self.parent[self.parent[node]]
node = self.parent[node]
return node
def findCircleNum(self, M):
"""
连通集个数
"""
self.initialize_tree(len(M))
for i in range(len(M)):
for j in range(i):
if M[i][j] == 1:
self.union(i, j)
return self.tree_num