均值、中值、高斯、non-local means算法详解
文章仅为个人理解，如有不妥之处欢迎指正。
写几个常见的图像去噪滤波器。
1、均值滤波器
均值滤波器是最简单的图像平滑滤波器，其3*3的模板为 1 9 [ 1 1 1 1 1 1 1 1 1 ] \frac{1}{9} \left[ \begin{matrix}1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{matrix} \right] 91⎣⎡111111111⎦⎤模板中心的滤波值是模板内像素点的平均值，过程如下图，填充几行由模板大小来决定。如果想滤波输出与原图像大小一致，填充是必须的，下文中就不再赘述了。
2、中值滤波器
中值滤波器是对模板内的像素值进行排序，然后选取中值作为模板中心的滤波值，均值噪声能有效去除椒盐噪声。
3、高斯滤波器
高斯滤波器是一种线性滤波器，能够有效的抑制噪声，平滑图像。其作用原理和均值滤波器类似，都是取滤波器窗口内的像素的均值作为输出。其窗口模板的系数和均值滤波器不同，均值滤波器的模板系数都是相同的为1；而高斯滤波器的模板系数，则随着距离模板中心的增大而系数减小。所以，高斯滤波器相比于均值滤波器对图像个模糊程度较小。
高斯模板的系数计算公式为： h ( △ x , △ y ) = e − △ x 2 + △ y 2 2 σ 2 h(\triangle x,\triangle y)=e^{-\frac{\triangle x^2+\triangle y^2}{2\sigma^2}} h(△x,△y)=e−2σ2△x2+△y2其中， △ x , △ y \triangle x,\triangle y △x,△y分别时模板内像素点到模板中心的相对距离。
以3*3高斯滤波器为例，取 σ = 0.8 \sigma=0.8 σ=0.8，其上式计算得模板系数为： [ 0.0521 0.1139 0.0521 0.1139 0.2487 0.1139 0.0521 0.11391 0.0521 ] \ \left[ \begin{matrix}0.0521 & 0.1139 & 0.0521 \\ 0.1139 & 0.2487 & 0.1139 \\ 0.0521 &0.11391 & 0.0521 \end{matrix} \right] ⎣⎡0.05210.11390.05210.11390.24870.113910.05210.11390.0521⎦⎤
需要注意的是，最后归一化的过程，使用模板左上角的系数的倒数作为归一化的系数（左上角的系数值被归一化为1），模板中的每个系数都乘以该值（左上角系数的倒数），然后将得到的值取整，就得到了整数型的高斯滤波器模板，就是我们常见的整数型3*3高斯滤波模板： 1 16 [ 1 2 1 2 4 2 1 2 1 ] \frac{1}{16}\left[ \begin{matrix}1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{matrix} \right] 161⎣⎡121242121⎦⎤高斯滤波器模板系数与标准差 σ \sigma σ有着很大的关系，当 σ \sigma σ取很小的值时，只有模板中心的值接近于1，其余的接近于0；当 σ \sigma σ取很大值时，模板系数全接近于1，相当于均值滤波。
上图可以看到，随着 σ \sigma σ的增大，图像去噪效果是明显了，但同时图像也更模糊了，这就需要我们在实际应用的时候平衡去噪效果和模糊程度。此外，模板尺寸越大，图像也会更模糊，去噪效果也会更好。
4、NLM算法
NLM全称为non-local means，顾名思义，它是非局部平均算法，上面几个算法都是利用滤波点周围几个像素点进行滤波，NLM对每个滤波点都利用了整张图像的信息。比如，要对像素点 i i i做NLM处理，先遍历整张图像，求出 i i i与其他像素点的相似度，相似度越大，权重越大，最后再对整张图像的像素点进行加权平均，就得到 i i i的滤波值。该方法充分利用了图像中的冗余信息，在去噪的同时能最大程度地保持图像的细节特征。
定义：假设 v v v是带噪声的图像， v = { v ( i ) , i ∈ I } v=\{ v(i),i∈I\} v={v(i),i∈I}， N L ( i ) NL(i) NL(i)表示对像素点 i i i的滤波值，就有： N L ( i ) = ∑ j ∈ I w ( i , j ) v ( j ) NL(i)=\sum_{j∈I}w(i,j)v(j) NL(i)=j∈I∑w(i,j)v(j) 且 ， 0 ≤ w ( i , j ) ≤ 1 ， ∑ j ∈ I w ( i , j ) = 1 且，0≤w(i,j)≤1，\sum_{j∈I}w(i,j)=1 且，0≤w(i,j)≤1，j∈I∑w(i,j)=1其中， v ( j ) v(j) v(j)表示像素点 i i i的灰度值，注意 j ∈ I j∈I j∈I，要遍历整张图像， w ( i , j ) w(i,j) w(i,j)是 v ( j ) v(j) v(j)的权重，由 i , j i,j i,j两像素点之间的相似度来得到。
如果仅仅比较 i , j i,j i,j像素值来作为相似度的依据，不能正确反映 i , j i,j i,j的关系，所以算法提出者利用 N ( i ) , N ( j ) N(i),N(j) N(i),N(j)的欧式距离来衡量相似度， N ( i ) , N ( j ) N(i),N(j) N(i),N(j)分别表示 i , j i,j i,j领域像素点，邻域大小可以自己选择；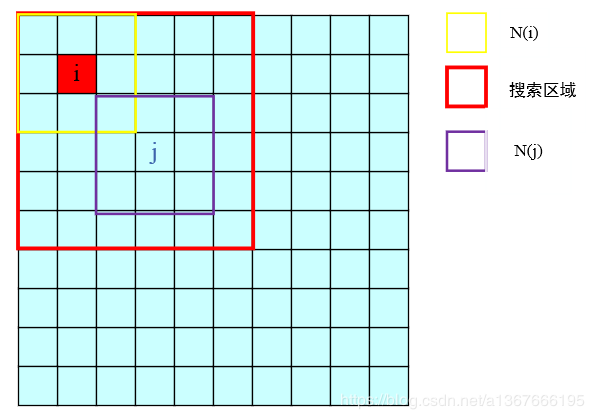
进一步就可以得到 w ( i , j ) = 1 C e ∣ ∣ N ( i ) − N ( j ) ∣ ∣ 2 h 2 w(i,j)=\frac{1}{C}e^{\frac{||N(i)-N(j)||_2}{h^2}} w(i,j)=C1eh2∣∣N(i)−N(j)∣∣2 C = ∑ j ∈ I e ∣ ∣ N ( i ) − N ( j ) ∣ ∣ 2 h 2 C=\sum_{j∈I}e^{\frac{||N(i)-N(j)||_2}{h^2}} C=j∈I∑eh2∣∣N(i)−N(j)∣∣2其中， ∣ ∣ N ( i ) − N ( j ) ∣ ∣ 2 ||N(i)-N(j)||_2 ∣∣N(i)−N(j)∣∣2就是欧式距离， h h h为滤波器参数，引入C是为了归一化。
由上式可以看出，当 i i i的邻域和 j j j的邻域相似度高的时候， v ( j ) v(j) v(j)的加权系数 w ( i , j ) w(i,j) w(i,j)也会比较大，下图中，明显可以看出 q 1 q1 q1点、 q 2 q2 q2点的邻域与 p p p点邻域比较相似，所以 w ( p , q 1 ) 、 w ( p , q 2 ) w(p,q1)、w(p,q2) w(p,q1)、w(p,q2)比较大，而 q 3 q3 q3的邻域与 p p p差别较大，所以 w ( q , p 3 ) w(q,p3) w(q,p3)就很小。
上面说过，对于每个 i i i,滤波值 N L ( i ) NL(i) NL(i)都需要用到整个的图像，这样就导致算法复杂度特别高，运算非常缓慢，所以通常在应用的时候，会选定一个搜索区域，在搜索区域内计算相似度，然后加权平均，而不是遍历整个图像了。
上面图像我选取邻域大小33，搜索区域77，小于论文原文使用的77邻域和2121搜索区域，即便如此，处理这幅512*512的图像也需要两分钟。
对于参数 h h h的选取，论文原文给出了选取规则， h = 10 σ h=10\sigma h=10σ， σ \sigma σ表示噪声标准差。但实际应用的时候，我发现 h h h的选取并不需要那么严格，只要别选的太大或者太小就行。 h h h很大的时候，NLM就接近于均值滤波器了。
5、 改进的NLM算法
针对NLM算法耗时太长的问题，论文Parameter-Free Fast Pixelwise Non-Local Means Denoising 提出了改进算法，在另一位博主文章积分图像的应用（二）：非局部均值去噪（NL-means）中对论文做了一定的解释，但是还是挺难懂的，我仅在此补充一些个人理解。在此之前你需要了解积分图像。
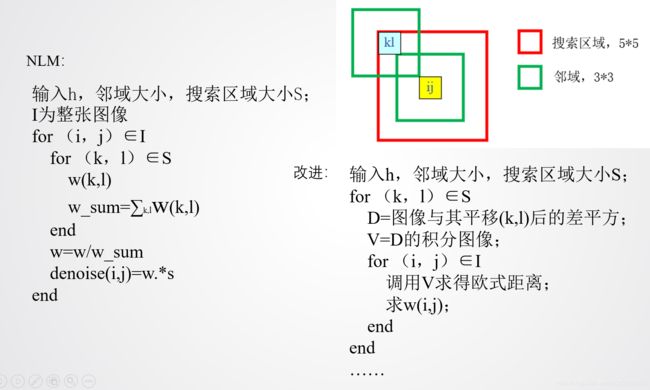上图中，左边是经典NLM算法流程，右边是改进后的大致流程。
我的理解：经典NLM对一个像素点点滤波完全结束后，才会进行对下一个像素点的滤波；而改进的NLM不是这样，它每次求出每个像素点邻域内的一个权重，而且相对位置（图中的 ( k , l ) (k,l) (k,l)）是一样的，然后遍历整个邻域位置，求出剩下权重，这样就得到了全部权重，在得到全部权重的同时，完成对整个图像的滤波，在此之前不会有任何像素点完成滤波，这一过程的实现需要用到积分图像。可以把经典NLM看成“串行”计算，那么改进NLM就是“并行”计算。
举个例子，看上图右上角的小图，经典NLM需要把邻域内25个权重都求出来，并且进行加权平均，才能对下一个像素进行滤波；改进的NLM每次求得所有像素点相对位置为 ( k , l ) (k,l) (k,l)那一像素值的权重。
上图是滤波结果图像，改进之后的NLM与经典NLM效果是一模一样的，但是耗时却大大下降了，因为核心思想是没变的，只是不同的实现过程。
用语言还是挺难完全说清楚的，以上只是帮助理解，想真正搞清楚还需要看代码，我把整篇文章的代码都放在这里了，可免费下载。