深度学习(二十七)——RBM & DBN & Deep Autoencoder
VAE(续)
正态分布?
对于 p ( Z ∣ X ) p(Z\mid X) p(Z∣X)的分布,是不是必须选择正态分布?可以选择均匀分布吗?
正态分布有两组独立的参数:均值和方差,而均匀分布只有一组。前面我们说,在VAE中,重构跟噪声是相互对抗的,重构误差跟噪声强度是两个相互对抗的指标,而在改变噪声强度时原则上需要有保持均值不变的能力,不然我们很难确定重构误差增大了,究竟是均值变化了(encoder的锅)还是方差变大了(噪声的锅)。而均匀分布不能做到保持均值不变的情况下改变方差,所以正态分布应该更加合理。
条件VAE
最后,因为目前的VAE是无监督训练的,因此很自然想到:如果有标签数据,那么能不能把标签信息加进去辅助生成样本呢?这个问题的意图,往往是希望能够实现控制某个变量来实现生成某一类图像。当然,这是肯定可以的,我们把这种情况叫做Conditional VAE,或者叫CVAE。(相应地,在GAN中我们也有个CGAN。)
但是,CVAE不是一个特定的模型,而是一类模型,总之就是把标签信息融入到VAE中的方式有很多,目的也不一样。这里基于前面的讨论,给出一种非常简单的VAE。
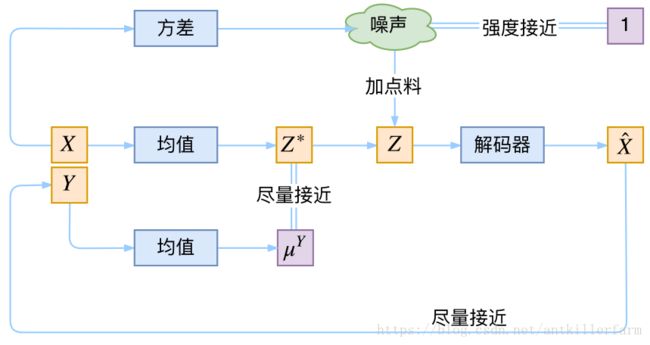
在前面的讨论中,我们希望X经过编码后,Z的分布都具有零均值和单位方差,这个“希望”是通过加入了KL loss来实现的。如果现在多了类别信息Y,我们可以希望同一个类的样本都有一个专属的均值 μ Y \mu^Y μY(方差不变,还是单位方差),这个 μ Y \mu^Y μY让模型自己训练出来。这样的话,有多少个类就有多少个正态分布,而在生成的时候,我们就可以通过控制均值来控制生成图像的类别。事实上,这样可能也是在VAE的基础上加入最少的代码来实现CVAE的方案了,因为这个“新希望”也只需通过修改KL loss实现:
L μ , σ 2 = 1 2 ∑ i = 1 d [ ( μ ( i ) − μ ( i ) Y ) 2 + σ ( i ) 2 − log σ ( i ) 2 − 1 ] \mathcal{L}_{\mu,\sigma^2}=\frac{1}{2} \sum_{i=1}^d\Big[\big(\mu_{(i)}-\mu^Y_{(i)}\big)^2 + \sigma_{(i)}^2 - \log \sigma_{(i)}^2 - 1\Big] Lμ,σ2=21i=1∑d[(μ(i)−μ(i)Y)2+σ(i)2−logσ(i)2−1]
VAE的另一个介绍
以下章节的内容主要摘自:
https://www.jeremyjordan.me/variational-autoencoders/
Variational autoencoders
该文中文版:
https://mp.weixin.qq.com/s/tRB85VF8XH9TTXZsiNVLhA
深入理解变分自编码器
自编码器是发现数据的一些隐状态(不完整,稀疏,去噪,收缩)表示的模型。 更具体地说,输入数据被转换成一个编码向量,其中每个维度表示从数据学到的属性。 最重要的是编码器为每个编码维度输出单个值, 解码器随后接收这些值并尝试重新创建原始输入。
变分自编码器(VAE)提供了描述隐空间观察的概率方式。 因此,我们不需要构建一个输出单个值来描述每个隐状态属性的编码器,而是要用编码器描述每个隐属性的概率分布。
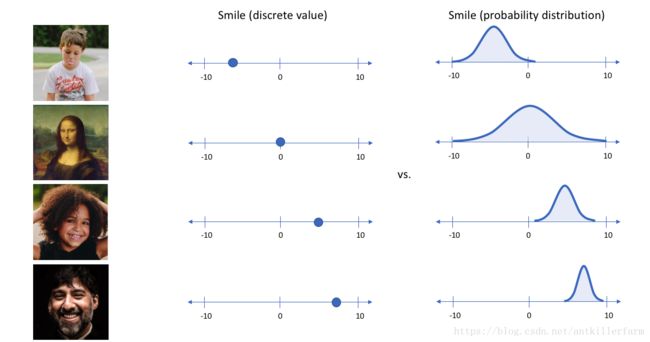
举个例子,假设我们已经在一个大型人脸数据集上训练了一个Autoencoder模型, encoder的维度是6。理想情况下, 我们希望自编码器学习面部的描述性属性,比如肤色,人是否戴眼镜,从而能够用一些特征值来表示这些属性。
在上面的示例中,我们使用单个值来描述输入图像的隐属性。 但是,我们其实更愿意用一个分布去表示每个隐属性。 比如, 输入蒙娜丽莎的照片,我们很难非常自信的为微笑属性分配一个具体值, 但是用了变分自编码器, 我们有能比较自信的说微笑属性服从什么分布。
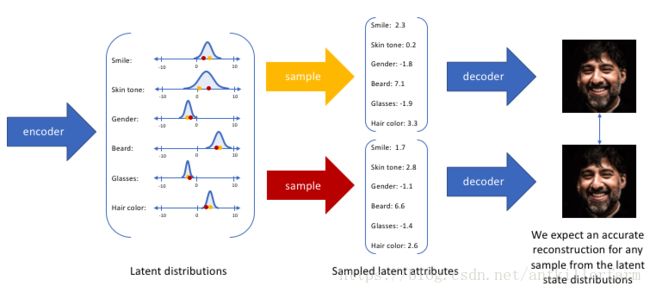
通过这种方法,我们现在将给定输入的每个隐属性表示为概率分布。 当从隐状态解码时,我们将从每个隐状态分布中随机采样,来生成向量作为解码器的输入。
通过构造我们的编码器来输出一系列可能的值(统计分布),然后随机采样该值作为解码器的输入,我们能够学习到一个连续,平滑的隐空间。因此,在隐空间中彼此相邻的值应该与非常类似的重建相对应。而从隐分布中采样到的任何样本,我们都希望解码器理解, 并准确重构出来。
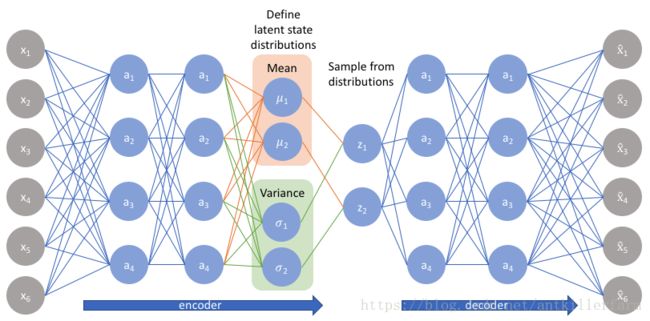
我们可以进一步将此模型构造成神经网络架构:
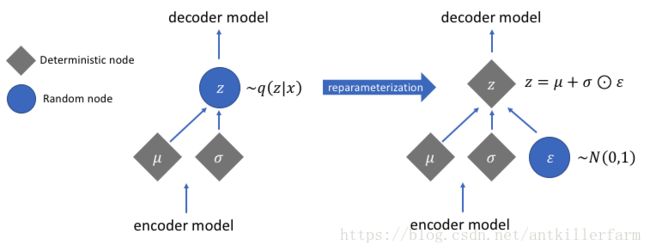
下图是VAE的结构图:
Reparameterization Trick的图示:
Reparameterization Trick的反向传播:
数值计算 vs 采样计算
VAE的基本概念到此差不多了,苏剑林趁热打铁又写了以下理论文章:
https://kexue.fm/archives/5343
变分自编码器(二):从贝叶斯观点出发
特将要点摘录如下。
对于不是很熟悉概率统计的读者,容易混淆数值计算和采样计算的概念。
已知概率密度函数p(x),那么x的期望也就定义为:
(1) E [ x ] = ∫ x p ( x ) d x \mathbb{E}[x] = \int x p(x)dx\tag{1} E[x]=∫xp(x)dx(1)
如果要对它进行数值计算,也就是数值积分,那么可以选若干个有代表性的点 x 0 < x 1 < ⋯ < x n x_0 < x_1 < \dots < x_n x0<x1<⋯<xn,然后得到:
(2) E [ x ] ≈ ∑ i = 1 n x i p ( x i ) ( x i − x i − 1 x n − x 0 ) \mathbb{E}[x] \approx \sum_{i=1}^n x_i p(x_i) \left(\frac{x_i - x_{i-1}}{x_n - x_0}\right)\tag{2} E[x]≈i=1∑nxip(xi)(xn−x0xi−xi−1)(2)
如果从p(x)中采样若干个点 x 1 , x 2 , … , x n x_1,x_2,\dots,x_n x1,x2,…,xn,那么我们有:
(3) E [ x ] ≈ 1 n ∑ i = 1 n x i , x i ∼ p ( x ) \mathbb{E}[x] \approx \frac{1}{n}\sum_{i=1}^n x_i,\quad x_i \sim p(x)\tag{3} E[x]≈n1i=1∑nxi,xi∼p(x)(3)
我们可以比较(2)跟(3),它们的主要区别是(2)中包含了概率的计算而(3)中仅有x的计算,这是因为在(3)中 x i x_i xi是从p(x)中依概率采样出来的,概率大的 x i x_i xi出现的次数也多,所以可以说采样的结果已经包含了p(x)在里边,就不用再乘以 p ( x i ) p(x_i) p(xi)了。
生成模型近似
对于二值数据,我们可以对decoder用sigmoid函数激活,然后用交叉熵作为损失函数,这对应于 q ( x ∣ z ) q(x\mid z) q(x∣z)为伯努利分布;而对于一般数据,我们用MSE作为损失函数,这对应于 q ( x ∣ z ) q(x\mid z) q(x∣z)为固定方差的正态分布。
苏剑林稍后还写了以下两文,都很值得一看:
https://kexue.fm/archives/5332
基于CNN和VAE的作诗机器人:随机成诗
https://kexue.fm/archives/5383
变分自编码器:这样做为什么能成?
参考
https://mp.weixin.qq.com/s/TqZnlXLKHhZn3U29PlqetA
变分自编码器VAE面临的挑战与发展方向
https://mp.weixin.qq.com/s/mtZ4_pwl8_GhitgImAU0VA
一文读懂什么是变分自编码器
https://mp.weixin.qq.com/s/LQFuXgI7uZK2UKRfZvlVbA
Variational AutoEncoder
https://mp.weixin.qq.com/s/lnSMdOk8fYfdU4aGeI5j7Q
未标注的数据如何处理?一文读懂变分自编码器VAE
https://zhuanlan.zhihu.com/p/27549418
花式解释AutoEncoder与VAE
https://mp.weixin.qq.com/s/ZlLuhu08m_RnD-h86df8sA
清华大学提出SA-VAE框架,通过单样本/少样本学习生成任意风格的汉字
https://mp.weixin.qq.com/s/t4YYIl4o_TAPG7737ZfiaA
面向无监督任务:DeepMind提出神经离散表示学习生成模型VQ-VAE
https://mp.weixin.qq.com/s/TJDGZvAvT7KamR_WN-oYYw
如何使用变分自编码器VAE生成动漫人物形象
https://mp.weixin.qq.com/s/6G1y2xMclUyzz_GQzKDrIw
变分U-Net,可按条件独立变换目标的外观和形状
https://mp.weixin.qq.com/s/1q36Cb4Fy4Mg7DcrAcJv3A
双人协作游戏带你理解变分自编码器-Part1
https://mp.weixin.qq.com/s/zJf-dWsMe5WELgDz7TlivA
双人协作游戏带你理解变分自编码器-Part2
https://mp.weixin.qq.com/s/fzadP8NwPTxuhEB0O4GU8g
漫谈生成模型,从AE到CVAE-GAN
RBM & DBN & Deep Autoencoder
RBM
Restricted Boltzmann Machines由 Hinton 发明,是一种用于降维、分类、回归、协同过滤、特征学习和主题建模的算法。
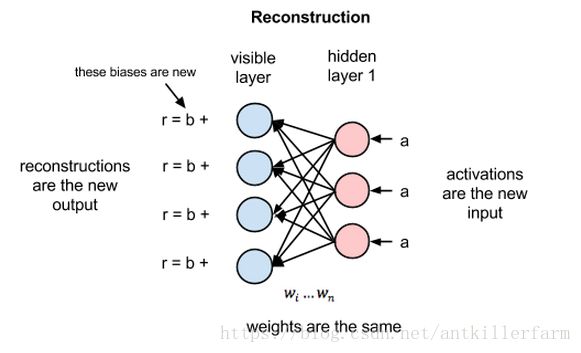
在重构阶段,第一隐藏层的激活值成为反向传递中的输入。这些输入值与同样的权重相乘,每两个相连的节点之间各有一个权重,就像正向传递中输入x的加权运算一样。这些乘积的和再与每个可见层的偏差相加,所得结果就是重构值,亦即原始输入的近似值。这一过程可以用下图来表示:
由于RBM权重初始值是随机决定的,重构值与原始输入之间的差别通常很大。可以将r值与输入值之差视为重构误差,此误差值随后经由反向传播来修正RBM的权重,如此不断反复,直至误差达到最小。
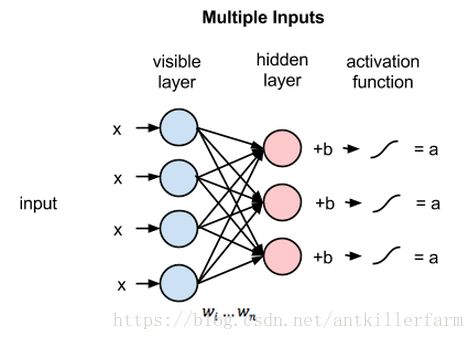
由此可见,RBM在正向传递中使用输入值来预测节点的激活值,亦即输入为加权的x时输出的概率: p ( a ∣ x ; w ) p(a\mid x; w) p(a∣x;w)。
但在反向传递时,激活值成为输入,而输出的是对于原始数据的重构值,或者说猜测值。此时RBM则是在尝试估计激活值为a时输入为x的概率,激活值的加权系数与正向传递中的权重相同。 第二个阶段可以表示为 p ( x ∣ a ; w ) p(x\mid a; w) p(x∣a;w)。
上述两种预测值相结合,可以得到输入x和激活值a的联合概率分布,即 p ( x , a ) p(x, a) p(x,a)。
重构与回归、分类运算不同。回归运算根据许多输入值估测一个连续值,分类运算是猜测应当为一个特定的输入样例添加哪种具体的标签。
而重构则是在猜测原始输入的概率分布,亦即同时预测许多不同的点的值。这被称为生成学习,必须和分类器所进行的判别学习区分开来,后者是将输入值映射至标签,用直线将数据点划分为不同的组。
RBM用KL散度来衡量预测的概率分布与输入值的基准分布之间的距离。
最后一点:你会发现RBM有两个偏差值。这是RBM与其他自动编码器的区别所在。隐藏的偏差值帮助RBM在正向传递中生成激活值(因为偏差设定了下限,所以无论数据有多稀疏,至少有一部分节点会被激活),而可见层的偏差则帮助RBM通过反向传递学习重构数据。
权重能够近似模拟出数据的特征后,也就为下一步的学习奠定了良好基础,比如可以在随后的有监督学习阶段使用深度置信网络来对图像进行分类。
RBM有许多用途,其中最强的功能之一就是对权重进行合理的初始化,为之后的学习和分类做好准备。从某种意义上来说,RBM的作用与反向传播相似:让权重能够有效地模拟数据。可以认为预训练和反向传播是实现同一个目的的不同方法,二者可以相互替代。