蓝桥杯 算法训练 最大的算式（Python实现 动态规划（一））

问题描述
　　题目很简单，给出N个数字，不改变它们的相对位置，在中间加入K个乘号和N-K-1个加号，（括号随便加）使最终结果尽量大。因为乘号和加号一共就是N-1个了，所以恰好每两个相邻数字之间都有一个符号。例如：
　　N=5，K=2，5个数字分别为1、2、3、4、5，可以加成：
$1\ast 2\ast (3+4+5)=24$
$1\ast (2+3)\ast (4+5)=45$
$(1\ast 2+3)\ast (4+5)=45$
　　……
输入格式
　　输入文件共有二行，第一行为两个有空格隔开的整数，表示N和K，其中（2<=N<=15, 0<=K<=N-1）。第二行为 N个用空格隔开的数字（每个数字在0到9之间）。
输出格式
　　输出文件仅一行包含一个整数，表示要求的最大的结果
样例输入
5 2
1 2 3 4 5
样例输出
120
样例说明
　　(1+2+3)x4x5=120

题目分析：

先说几句废话哈~昨天下午还不知道动态规划为何物的我昨天研究了一宿，终于在看了B站优秀视频（up主：正月点灯笼）和阅读了大佬们前辈们的优秀博客之后，我终于知道了一点儿皮毛，文中错误或疏漏之处欢迎各位大佬指点。动态规划是先解决子问题再逐步解决大问题。我们输入的量是一串数字和数个乘号，比如上面给的例子，输入5个数字（1,2,3,4,5），需要用2个乘号，我们每拿起一个数，就要拿起一个符号，按照题目给的，我们要么拿起乘号，要么不拿。下图粗略表现一下我的思路：

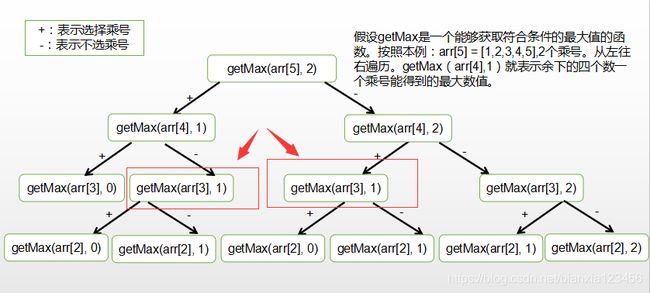
我们能看见，红色框出来的是一样的，我们可以把计算结果存储在一个地方，下次需要的时候就拿来用。
我们构建一个二维数组，数字个数(n)作为行，乘号个数(k)作为列，数组的每个值，在个数和乘号个数条件下面的最大值。依照题目里面的n=5,k=2。如下图：

	0	1	2
0	无	无	无
1		无	无
2			无
3
4
5

数字比符号少以及数字等于符号的时候肯定是没有结果的，直接写上无。
下面我们来一个一个算，我们把这个数组叫dp（dynamic programming）dp的尺寸应该是（n+1）*（k+1），比如dp[4][2]的值就代表前4个数，用两个乘号的最大值。我们先看第一列，就是k=0的时候，我们想，没有乘号的时候，最大值就是求和，所以我们第一列就是：

	0	1	2
0	无	无	无
1	1	无	无
2	3		无
3	6
4	10
5	15

然后我们来看第二列，第二列就是有一个乘号：
dp[2][1] = dp[1][0]x(dp[2][0] - dp[1][0]) = 1 x 2 = 2
dp[3][1] = dp[2][0]x(dp[3][0] - dp[2][0]) = （1+2）x 3 = 9

下一个dp[4][1]的时候出现了不同，可以是（1+2）x（3+4）也可以是（1+2+3）x4，这时候就需要max函数了，反正我们只要能够得到最大的就行。
①dp[4][1] = dp[3][0]x(dp[4][0] - dp[3][0]) = （1+2+3）x 4 = 24
②dp[4][1] = dp[2][0]x(dp[4][0] - dp[2][0]) = （1+2）x （3+4） = 21
取大，所以dp[4][1] = 24

同理在分析一个dp[5][1]:
①dp[5][1] = dp[1][0]x(dp[5][0] - dp[1][0]) = 14
②dp[5][1] = dp[2][0]x(dp[5][0] - dp[2][0]) = 36
③dp[5][1] = dp[3][0]x(dp[5][0] - dp[3][0]) = 54
④dp[5][1] = dp[4][0]x(dp[5][0] - dp[4][0]) = 50
取大，所以dp[5][1] = 54
dp[5][1] = dp[3][0]x(dp[5][0] - dp[3][0]) = （1+2+3）x（15-6）= 54

从上面的式子里面我们可以总结出来一个通式：
dp[5][1] = dp[4][0]*(dp[5][0] - dp[4][0])拿这个式子来说（我真的好啰嗦），dp[4][0]是四个数0个乘号的最优解，我们要的是dp[5][1]，所以加一个数，加一个乘号，dp[5][0] - dp[4][0]的值其实就是我们原来的列表里面的第五个数的值，我们用前面四个数0个乘号的最优解加上一个乘号在全局跑一遍，取得最大的就是本轮的最优解，以此类推。。。。（我不知道我说明白没，我希望我没有说错。。。）
所以，所以通式终于来了：
dp[i, j] = max(dp[i, j], dp[p, j - 1] * (dp[i, 0] - dp[p, 0]))
(1<=p dp数组如下：

	0	1	2
0	无	无	无
1	1	无	无
2	3	2	无
3	6	9	6
4	10	24	36
5	15	54	120

好了，下面用Python3来实现它：

import numpy as np
s = list(map(int, input().split()))
n, k = s[0], s[1]
num = [int(n) for n in input().split()]    #数组
temp = num[0]
dp = np.zeros([n+1,k+1], dtype = np.int)
dp[1,0] = num[0]
for i in range(1, n):
    temp += num[i]
    dp[i+1, 0] = temp
if k == 0:
    print(dp[n, k])
else:
    # 按照列遍历
    for j in range(1, k + 1):
        # 按照行
        for i in range(2, n + 1):
            if i > j:
                for p in range(1, i):
                    dp[i, j] = max(dp[i, j], dp[p, j - 1] * (dp[i, 0] - dp[p, 0]))
    print(dp[n, k])

就在我觉得大功告成的时候，蓝桥杯的在线评测显示0分，为啥呢，我不信。。。。蓝桥杯不能导入别的模块（我用了Numpy）(保持微笑)。。。抽时间再写一遍。

好了，不用numpy的来了，传送门
编程小白记录成长