算法4第6章 B+树讲解
B+数树是一种多叉平衡查找树,由于B+树对磁盘进行IO操作更加合理高效,所以许多数据库系统都使用这种数据结构来实现索引.
多叉是相对二叉树而言,平衡是指从根节点到所有叶子节点的路径长度是一样的,查找是指一个非叶子节点所有左边节点的值
都比右边节点的值要小。
B+树还有以下主要特性:
1.假设每个节点可以存M个关键字,则每个节点最多有M+1个子节点.
2.关键字对应的信息只存在叶子节点,非叶子节点只存到子节点的索引
3.所有叶子节点用双向链表连接
具体我们通过对B+树增删改查实现的讲解,来了解B+树的所有特性。
假设树的每个节点用一个page表示,每个page都有一个pageheader,如下图中的PH,PH里放一个firstpage指针,用来指向第1个子page
每个page可以存2个节点信息,节点信息大概可以表示如下,则每个非叶子page最多有3个子page.(实际操作时一个page里可以放很多节点信息)
struct Node {
int key; //关键字
int value; //关键字对应的值
int page_num; //指向子page
};
B+树的插入过程:
我们依次插入关键字2,5,1,3,4,
开始分配一个page1作为根节点,插入关键字2,5,关键字要按从小到大的顺序排列 如图1,
然后插入关键字1时,根page1已满,分配一个新page2作为根节点,page2的pH里的firstpage指向page1,
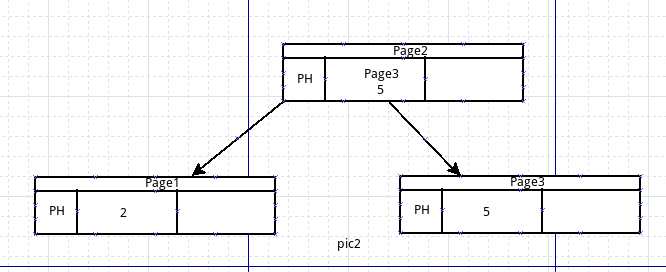
page1分裂出一个新的page3节点,page1的一半节点copy到page3里,这样5被放到page3里,根page2的第1个Node里的key放5,page_num指向子page3.如图2,
分裂完后开始插入关键字1,如果是根page分裂后,则从根page开始插入,如果是中间节点分裂后,则从分裂的中间节点那里插入,
直到插入到一个叶子page里,1与5比较,小一些应该从左边的page1插入,page1又是叶子,所以1放到page1里,page1排序下如图3所示。
然后开始插入3,从根page2开始,page2没有满并且不是叶子节点,所以要插入到它的子page中,3与5比较,小所以应该插入到左边的子page1中,
这时发现子page1已满,从page1分裂出一个新的page4节点,关键字2的节点信息copy到page4,page4做为根page2的新子page, 如图4所示,
分裂完成后,关键字3与page4里的第1个关键字2比较,大于等于2大则放入page4,比2小则放入左边的page1, 3比2大所以放入page4.如图5.
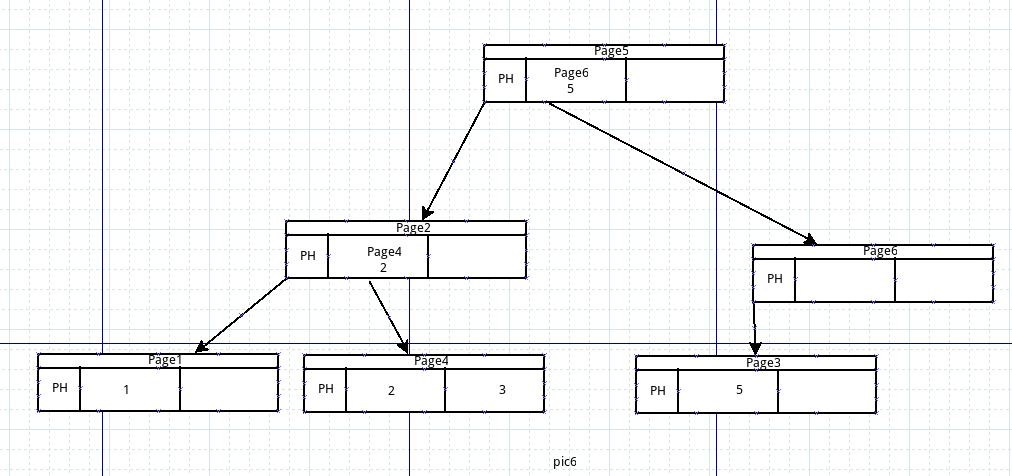
然后开始插入关键字4,也是从根page2开始,发现根page2已满,就要分配一个新page5作为根节点,page5的pH里的firstpage指向原来的根page2,
page2分裂出一个新的page6,page2中的一半节点信息copy到page6,则关键字5及其子page3 copy到page6,page6作为根page5新的子page
由于page6为空,所以只用page6的PH指向page3,如图6.
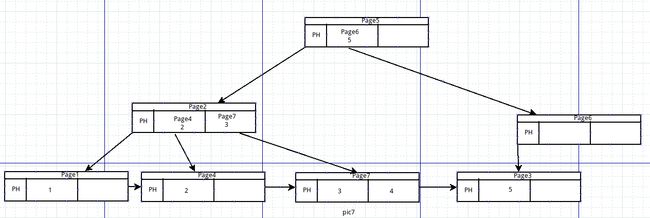
分裂完后开始插入4,分裂的是根page,则从根page5开始,page5没有满并且不是叶子节点,4比5小移到左边的page2, 发现page2没有满并且不是叶子节点,4与2比较,大一些移到右边的page4,
发现page4已满,page4分裂出新的page7作为page2的子节点,4插入page7,如图7所示,每一步操作所有叶子节点都是用双向链表连起来的