数字图像处理——第十一章（表示和描述）

参考https://blog.csdn.net/mary_0830/article/details/89703255
参考https://blog.csdn.net/zcg1942/article/details/81771991
参考https://blog.csdn.net/Arthur_Holmes/article/details/98661377

将一幅图像分割成多个区域后，分割后的像素集经常以一种合适于计算机进一步处理的形式来表示和描述。

表示
表示一个区域的两种选择：

• 根据区域外部特征（如边界）来表示区域-
• 根据内部特征（如组成该区域的像素）来表示区域

表示是直接具体地表示目标，好的表示方法应具有节省存储空间易于特征计算等优点。
表示的下一步工作是描述。表示方式的选择要使数据有利于描述工作的展开。
当关注的重点是形状特征时，可选择外部表示；当关注的重点是内部属性（如颜色和纹理）时，可选择内部表示。

描述
描述是较抽象地表示目标。好的描绘子都应尽可能对目标的大小、平移、旋转等不敏感，这样的描绘子比较通用。

表示和描述应该是个递进的关系，表示旨在以更（精确/方便/高效）的方式组织数据，而描述旨在从表示中总结某种模式以便于任务的完成。表示侧重于数据结构，而描述侧重于区域特性以及不同区域间的联系和差别。
常见的图像特征分为灰度、纹理和几何形状等。其中，灰度和纹理属于内部特征，几何形状属于外部特征。

一、基础知识

元胞数组（cell）和结构体（structure）

元胞数组

元胞数组提供了一种将各种类型的对象（如数字、字符、矩阵和其他元胞数组）组合在一个变量名下的方法。
创建
通过赋值语句直接创建；或通过cell函数首先为元胞数组分配内存空间，然后再对每个元胞赋值。

% 通过赋值语句直接创建
>> f = imread('building.tif');
>> % 元胞索引赋值
>> A(1,1) = {f};
>> A(1,2) = {{'area','centroid'}};
>> A(2,1) = {[1 4 2; 3 4 5; 0 5 7]};
>> A(2,2) = {1:2:19};
>> A
A =
  2×2 cell 数组
    {601×601 uint8 }    {1×2  cell  }
    {  3×3   double}    {1×10 double}

>> % 内容索引赋值
>> B{1,1} = [1 3;69 90];
>> B{1,2} = 'lavender';
>> B{1,3} = 1 + 2i;
>> B
B =
  1×3 cell 数组
    {2×2 double}    {'lavender'}    {[1.0000 + 2.0000i]}

% 通过cell函数分配内存空间再进行赋值
>> C = cell(2,2);
>> C(1,2) = {[1 2 3;4 5 6;7 8 9]};
>> C(2,2) = {'amazing'};
>> C
C =
  2×2 cell 数组
    {0×0 double}    {3×3 double}
    {0×0 double}    {'amazing' }

访问

% 通过圆括号可以访问元胞数组的每个元胞
>> C(1,2)
ans =
  1×1 cell 数组
    {3×3 double}
%  通过花括号可以访问元胞数组的每个元胞中的具体内容
>> C{2,2}
ans =
    'amazing'

函数size可以获得元胞数组的大小
函数cellfun

D = cellfun('fname',A)
将函数fname应用于元胞数组A的元素，返回结果为双精度数组D。数组D中的每个元素包含有由fname返回的与A中元素相对应的值。输出数组D与元胞数组A的大小相同。

>> D = cellfun('length',A)
D =
   601     2
     3    10

length(A)给出多维数组A中的最长维数的尺寸。
注： 元胞数组包含的是变量的副本，而不是指向这些变量的指针。上述例子中A中的任何变量在A创建后改变，改变不会在A中体现。

结构体

结构体（structure）和元胞数组非常相似，也是将不同类型的数据集中在一个单独变量中，结构体通过字段来对元素进行索引，在访问时只需通过点号来访问数据变量，结构体可以通过两种方法进行创建：直接赋值创建或通过struct函数来创建。

% 创建
>> circle.radius=3.0;
>> circle.color='red';
>> circle.center=[5 8];
% 访问
>> circle.color
ans =
    'red'

本章使用的一些matlab和IPT函数

• imfill函数：填充图像区域和孔洞。对于二值图像和灰度图像的作用不同。

参考imfill

% 二值图像
gB = imfill(fB,locations,conn)
在输入二值图像fB的背景像素上从参数locations指定的点开始，执行填充操作（即，将背景像素值设置为1）。
locations：可以是n*1的向量（n为位置的数目）向量包含起始位置的线性索引；也可以是n*2的矩阵，矩阵中的每行包含有fB中的一个起始位置的二维坐标。
conn：指定背景像素使用的连接方式：4（默认）或8

gB = imfill(fB,conn,'holes')  % 填充输入二值图像中的孔洞。孔洞是一个背景像素集合，不能通过图像边缘来填充背景达到这一目的。

% 灰度图像
g = imfill(fI,conn,'holes') % 填充输入灰度图像fI的孔洞。该情况下，孔洞是指较亮像素包围的暗像素区域。填充的结果就是将被包围的暗像素置为1。

• bwlabel——对二维二值图像中的连通分量进行标记（得到标记图像）

[L,n] = bwlabel(BW,conn)  % 对二维二值图像中的连通分量进行标记
BW：二值图像
conn：像素的连通性：4或8（默认）
n：连通分量的个数
L：标记矩阵。与 BW 大小相同的非负整数矩阵。标记为 0 的像素构成背景。标记为 1 的像素构成一个对象；标记为 2 的像素构成另一个对象；等等。

• find——返回构成某个指定对象（连通分量或区域）像素的坐标向量。可以与bwlabel函数一起使用。若bwlabel产生了多个连通分量（即n>1）。则可使用下面的语法获得某个连通分量（区域）的坐标：

[r,c] = find(bwlabel(BW)==2)   % 返回连通分量2中的像素坐标

本章中，某个区域或边界的二维坐标被表示成np*2数组的形式，其中每行是一个(x,y)坐标对，np是区域或边界中的包含的点的个数。在某些情况下，有必要对数组进行排序。

• sortrows——对数组进行排序

z = sortrows(S) %对数组S的行进行排序。
S必须是矩阵或列向量。本章中，函数sortrows只与np*2数组一起使用。若一些行的第一坐标相同，则按第二坐标升序排序。

• unique函数——既想对数组S的行排序，又要去除重复行

[z,m,n] = unique(S,'rows')
z：排序后无重复行的数组，m和n是z = S(m,:)和S  = z(n,:)。即m用来指示数组S中的哪些行被保留，n用来指示数组S中的每一行对应在z中的哪一行

>> S = [1 2;6 5;1 2;4 3];
>> [z,m,n] = unique(S,'rows');
>> z
z =
     1     2
     4     3
     6     5
>> m
m =

     1
     4
     2
>> n
n =
     1
     3
     1
     2

• circshift——对数组行进行向上、向下或侧移指定位置数的移位操作

z = circshift(S,[ud lr])
ud是S向上或向下移位的元素数，若ud为正，则向下移动ud个元素，反之，向上；lr是S向左向右移位的元素数，lr为正，向右，反之，向左。上下移动时是将数组或矩阵看成一个首尾相接的圈来移动的。
z = circshift(S,ud)  % 只进行上下移位操作

>> S = [1 2;6 5;1 2;4 3];
>> z = circshift(S,[1 1])
z =
     3     4
     2     1
     5     6
     2     1

若S是一幅图像，则circshift就是对图像进行的卷动操作（向上和向下）或平移操作（向左和向右）。

基本的M函数

如上所述，边界或区域已被表示为np x 2数组，数组中的每一行表示一个(x,y)坐标对。下面介绍的函数中，大部分会自动地将大小为2 x np的坐标数组转换为大小为np x 2的数组。

• 自定义函数boundaries——获得图像中对象（区域）的外部边界坐标

B = boundaries(f,conn,dir)  % 跟踪f中对象的外部边界。
f：假设为二值图像，其背景像素为0
conn：输出边界的连接方式。值为4或8（默认）
dir：指明边界被跟踪的方向，其值可为'cw'（顺时针，默认）或'ccw'（逆时针）方向
B：一个元胞数组，每个元素对应一个已找到的对象的边界的坐标集合。通过访问B{1}可得到第一个区域对应的边界坐标集合b，b的大小为np*2，访问第二个第三个是类似的。
由函数boundaries返回的边界中第一个点和最后一个点相同，将产生一个闭合边界。

• bwboundaries——跟踪二值图像中的区域边界坐标

B = bwboundaries(f,conn,options)
bwboundaries 还能跟踪最外层对象（父对象）及其子对象（完全被父对象包围的对象），对象即区域。
f：二值图像
conn：边界连通性，4或8（默认）
options：'holes'（默认）：同时搜索对象和孔洞边界；'noholes'：仅搜索对象（父对象和子对象）边界
或 [B,L] = bwboundaries(f,conn,options)   %L是标记矩阵
或 [B,L,n,A] = bwboundaries(f,conn,options)   %n是找到的对象的数量，A是逻辑稀疏矩阵

• 自定义函数bound2eight——从边界中移出4连通的像素，剩下8连通的像素。

b8 = bound2eight(b);
输入b必须是一个大小为np*2的矩阵，它的每一行包含一个边界像素的(x,y)坐标，要求b是闭合的，连接的像素集合按顺时针方向或逆时针方向排列

• 自定义函数bound2four——从边界中移出8连通的像素，仅留下4连通的像素。

b4 = bound2four(b);
输入b必须是一个大小为np*2的矩阵，它的每一行包含一个边界像素的(x,y)坐标，要求b是闭合的，连接的像素集合按顺时针方向或逆时针方向排列

• 自定义函数bound2im——用于构建和显示一幅包含感兴趣区域边界的二值图像。

g = bound2im(b,M,N,x0,y0) 
g：二值图像，图像大小为M*N,边界点为1，背景为0.
x0和y0：决定图像中b的最小x和y坐标位置。
b：一个大小为np*2的数组，np为边界像素数，每一行包含一个边界像素的坐标
若x0和y0被省略，则在M*N数组中边界会被近似中心化
若M和N被省略，则图像的水平和垂直尺度就等于边界b的长度和宽度。
若函数boundaries发现多个边界，可使用函数bound2im，通过连接元胞数组B的元素，获得对应的所有坐标
b = cat(1,B{:})  % 参数1表示沿数组的第一（垂直）维进行级联。

• 自定义函数bsubsamp——对边界进行二次取样

[s, su] = bsubsamp(b,gridsep)
在一个网格上对单一边界b二次取样，网格线由gridsep像素分离。
输出s是一个比b有更少的点的边界。点的数目由gridsep的值确定，su是按比例取得的边界点的集合。

• 自定义函数connectpoly——将bsubsamp对边界二次取样后的点连接起来

z = connectpoly(s(:,1),s(:,2)) 
s的行是二次取样后的边界的坐标。要求s中的点按顺时针或逆时针方向排列。
z的行是连接边界的坐标，它是通过连接s中的使用4或8连接直线段的最短可能路径的点而成的。

• 函数intline——计算连接两点的一条直线的整数坐标

[x,y] = intline(x1,x2,y1,y2)
(x1,y1)和(x2,y2)分别是两个待连接点的整数坐标。
x和y是列向量，它包含连接两点的一条直线的x坐标和y坐标

二、表示

分割技术会获得原始数据，其形式是沿着边界或包含在区域中的像素。标准做法是使用某种方案将分割后的数据精简为便于描绘子计算的表示。
以下介绍的算法要求一个区域的边界上的点以顺时针（或逆时针）方向排序。

链码

链码通过具有指定长度和方向的直线段的顺次连接来表示边界。该表示基于线段的4连接或8连接。每个线段的方向用数字编码方案编码。也称为佛雷曼链码。

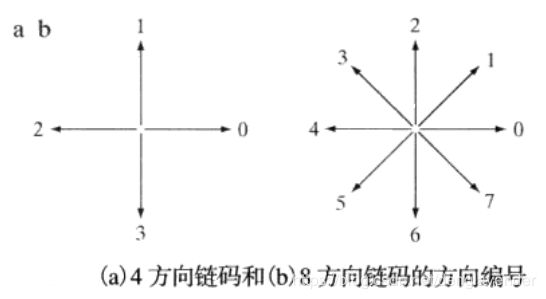
算法：给每个线段一个方向编码（4方向和8方向两种），从起点开始，沿边界进行编码，至起点被重新碰到，一个对象的编码完成。
问题：链码过长；噪声或不完美分割会产生不必要的链码。
解决：选取较大的网格间距对边界重取样，依据原始边界与结果的接近程度，确定新点的位置。

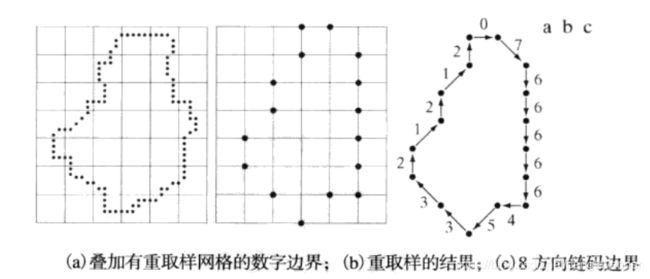
边界的链码取决于起点。
起点归一化：将链码视为方向号码的一个循环序列，并重新定义起点，选择其中最小值整数序列作为最终编码（将编码作为自然数进行比较，前面0最多的就是最小的）。
旋转归一化：使用链码的一次差分。

• 若差分是通过计算链码中分割两个相邻像素的方向变换次数得到的。如4方向链码（按逆时针方向）10103322的一次差分为3133030。具体算法：逆时针从1->0需要3步，逆时针从0->1需要1步，逆时针从1->0需要3步，逆时针从0->3需要3步，以此类推。
• 若将链码作为循环序列，则差分的第一个元素是通过使用链码的最后一个元素和第一个元素间的转变得到的，此时4方向链码（按逆时针方向）10103322的一次差分为33133030。具体算法：逆时针从2->1需要3步，再接着依次计算从1->0，从0->1等等。

当使用链码表示一条边界时，通常需要进行边界平滑。

fchcode函数

c = fchcode(b,conn,dir)  % 计算保存在数组b中的np*2个已排序边界点集的Freeman链码

c：是包含以下域的结构，圆括号的数字表示数组的大小：
		c.fcc = Freeman链码(1 x np)
		c.diff = c.ffc的一阶差分链码(1 x np)
		c.mm = 最小值整数链码(1 x np)
		c.diffmm = 链码c.mm的一阶差分(1 x np)
		c.x0y0 = 链码的起点坐标(1 x 2)
conn：链码的连接方式，4或8（默认）。当边界不包含对角转换时，值设为4才是有效的。
dir：指定输出链码的方向，'same'（默认）：链码方向和b中的点的方向相同；'reverse'：链码方向与b中的点的方向相反

链码一般用于一幅图像中有多个对象的情况。
示例：获得图像的最大物体外部边界的最小值整数的佛雷曼链码和其一阶差分

f = imread('noisy_circular_stroke.tif');
figure;subplot(2,2,1),imshow(f),title('(a)带噪原图');

h = fspecial('average', 9);
g = imfilter(f, h ,'replicate');  % 因为感兴趣的是粗边界，所以进行平滑处理可有效抑制噪声
subplot(2,2,2),imshow(g),title('(b)均值模板平滑处理结果');

T = graythresh(g);
gB = imbinarize(g,T);  % 使用Ostu方法对图像进行阈值处理
subplot(2,2,3),imshow(gB),title('(c)Ostu方法对平滑图像阈值的结果');

B = boundaries(gB);  % 提取图像边界
d = cellfun('length',B);
[max_d, k] = max(d); % k是最长边界对应的区域数
b = B{k(1)}; % 得到最长边界的坐标

[M,N] = size(g);
g = bound2im(b,M,N,min(b(:,1)),min(b(:,2)));  % 构建最长边界对应的二值图像
subplot(2,2,4),imshow(g),title('(d)图c的最长外部边界');

[s,su] = bsubsamp(b,50);  % 对最长边界二次取样,节点间距为50像素（约为图像宽度的10%，图像宽度为570）
g2 = bound2im(s,M,N);  % 构建取样后的边界对应的二值图像
figure;imshow(g2),title('(e)对最长边界取样后的边界图像');

cn = connectpoly(s(:, 1),s(:, 2));  % 对取样后边界进行连接
g3 = bound2im(cn,M,N,min(cn(:,1)),min(cn(:,2)));  % 将感兴趣的边界显示为二值图像
figure; imshow(g3),title('(f)对取样后的点进行连接');

c = fchcode(su);  %产生链码

为了可以看清楚取样后的边界点及其连接，将它们单独进行了显示。



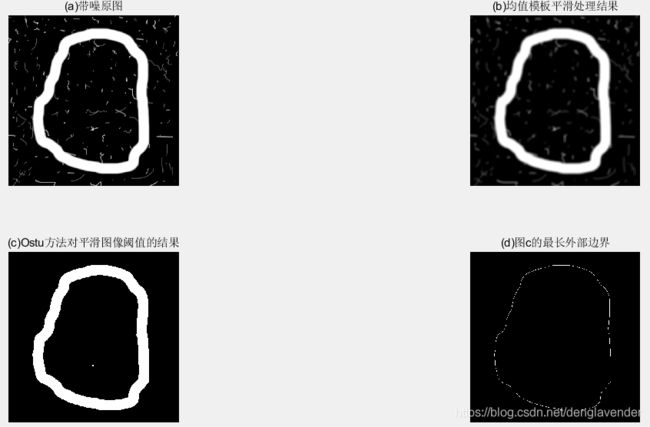
其中取样后的最大物体外部边界的最小值整数链码c.mm和其一次差分c.diff如下：

>> c.x0y0
ans =
     8     3     
>> c.mm
ans =
     0 0 0 0 6 0 6 6 6 6 6 6 6 6 4 4 4 4 4 4 2 4 2 2 2 2 2 0 2 2 0 2
>> c.diff
ans =
     0 0 6 2 0 6 2 6 0 0 0 6 2 6 0 0 0 0 0 0 0 6 0 0 0 0 0 6 2 6 0 0

使用最小周长多边形的多边形近似

数字边界可以用多边形以任意精度来近似。对一条闭合边界，当多边形的边数等于边界上的点数时，该近似就会很精确，此时每对相邻点定义了多边形的一条边。多边形近似的目的是用尽可能少的线段获取给定边界的基本形状。实际中，很有效的近似技术是用最小周长多边形（MPP）来表示边界。

所有MPP的顶点与多边形边界的内墙或外墙（图中的浅灰色边界）的角点一致。边界由4连接的直线段组成。多边形的凸顶点和凹顶点分别用白点和黑点表示。只有内墙的凸顶点和外墙的凹顶点才能成为MPP的顶点。

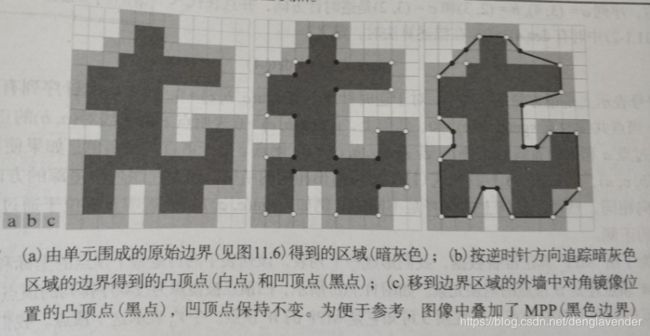
围成一条数字边界的单元集合称为单元组合体。

自定义函数minperpoly来实现MPP算法。只能处理单一区域或边界。调用格式如下：

[X, Y] = minperpoly(f,cellsize)
f是一幅包含单一区域或边界的二值图像，cellsize是指定用于围绕边界的单元组合体中方形块的大小。X和Y包含MPP顶点的x和y坐标。

示例

f = imread('mapleleaf.tif');
figure; subplot(2,4,1),imshow(f),title('原始图像');
B = boundaries(f,4,'cw');  % 获得图像边界，B为元胞数组
b = B{1}; % b为边界点坐标，np*2大小的

xmin = min(b(:,1));
ymin = min(b(:,2));
[M,N] = size(f); 
bim = bound2im(b,M,N,xmin,ymin);  % 用边界构建二值图像
subplot(2,4,2),imshow(bim),title('4连接边界的图像');

[X,Y] = minperpoly(f,2);  % 获得MPP顶点坐标
b2 = connectpoly(X,Y); % 连接顶点形成边界
bCcellsize2 = bound2im(b2,M,N,xmin,ymin); % 用边界构建二值图像
subplot(2,4,3),imshow(bCcellsize2),title('使用大小为2的方形单元组合体得到的MPP');

[X,Y] = minperpoly(f,3);
b3 = connectpoly(X,Y);
bCcellsize3 = bound2im(b3,M,N,xmin,ymin);
subplot(2,4,4),imshow(bCcellsize3),title('使用大小为3的方形单元组合体得到的MPP');

[X,Y] = minperpoly(f,4);
b4 = connectpoly(X,Y);
bCcellsize4 = bound2im(b4,M,N,xmin,ymin);
subplot(2,4,5),imshow(bCcellsize4),title('使用大小为4的方形单元组合体得到的MPP');

[X,Y] = minperpoly(f,8);
b8 = connectpoly(X,Y);
bCcellsize8 = bound2im(b8,M,N,xmin,ymin);
subplot(2,4,6),imshow(bCcellsize8),title('使用大小为8的方形单元组合体得到的MPP');

[X,Y] = minperpoly(f,16);
b16 = connectpoly(X,Y);
bCcellsize16 = bound2im(b16,M,N,xmin,ymin);
subplot(2,4,7),imshow(bCcellsize16),title('使用大小为16的方形单元组合体得到的MPP');

[X,Y] = minperpoly(f,32);
b32 = connectpoly(X,Y);
bCcellsize32 = bound2im(b32,M,N,xmin,ymin);
subplot(2,4,8),imshow(bCcellsize32),title('使用大小为32的方形单元组合体得到的MPP');

枫叶有两个主要的特征：茎和三个主要的圆裂片。
使用大于22的单元时，降低的分辨率，导致了细茎的消失。而即使是1616大小的单元，三个圆裂片的特征仍保留的比较完整。当单元大小增大到32*32时，圆裂片特征也几乎消失。
原始边界中的点数为1499 。单元大小为2~32的边界中的点数分别为1081，930 ，895， 819，765，677。使用1081个顶点的图©保留了原始边界的所有主要特征。故可以看出使用MPP来表示边界的优势。MPP的另一个优点是可以进行边界平滑。

标记

标记是边界的一维函数表示。一种最简单的生成方法是以角度函数形式画出质心到边界的距离。如下图所示

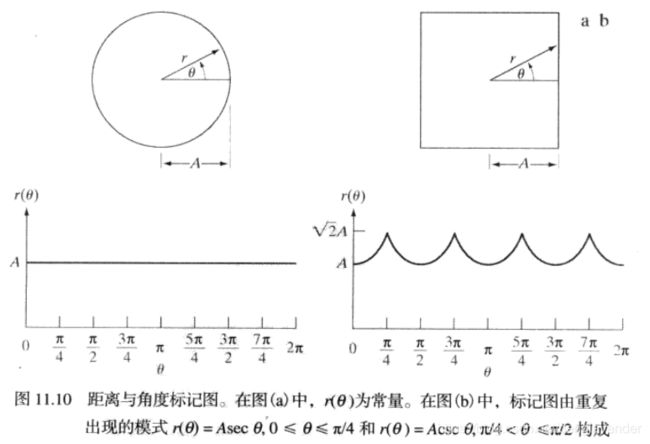
无论如何生成标记，基本思想都是将边界表示简化为比原始二维边界更简单的一维函数。

自定义函数signature——查找给定边界的标记。

[dist,angle,x0,y0] = signature(b,x0,y0)
b：一个大小为np*2的数组，包含一条按顺时针或逆时针方向排列边界的坐标，b必须是1像素宽的边界，使用boundaries函数或bwboundaries函数就能得到。
(x0, y0)：是一个点的坐标，若不给出，则默认使用边界的质心坐标。测量该点到边界的距离。
dist：(x0, y0)点到边界的距离。随着角度angle的变化，距离不断变化。
dist和angle大小为360*1。
输出的(x0,y0)：当输入的指定了(x0,y0)时，输出的也是该值，当输入不指定时，输出返回的是边界的质心坐标

signature需要使用matlab自带函数cart2pol——将笛卡尔坐标转换为极坐标

[THETA, RHO] = cart2pol(X, Y)

对应的，pol2cart——将极坐标转换为笛卡尔坐标

[X,Y] = pol2cart(THETA,RHO)

示例

fsq = imread('boundary_sq.tif');
ftr = imread('boundary_triangle.tif');

bsq = bwboundaries(fsq,'noholes');
[distSq,angleSq] = signature(bsq{1});

btr = bwboundaries(ftr,'noholes');
[distTr,angleTr] = signature(btr{1});
figure;
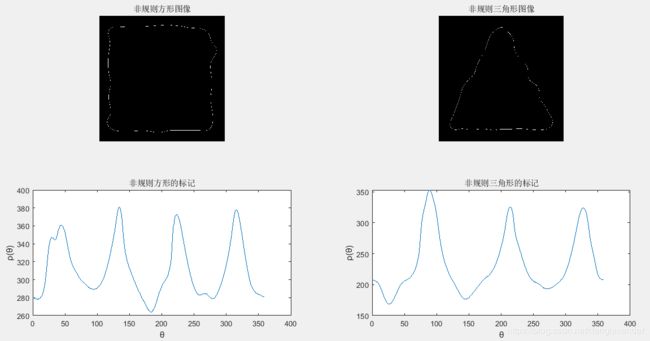
subplot(221),imshow(fsq),title('非规则方形图像');
subplot(222),imshow(ftr),title('非规则三角形图像');
subplot(223),plot(angleSq,distSq),xlabel('θ'),ylabel('ρ(θ)'),title('非规则方形的标记');
subplot(224),plot(angleTr,distTr),xlabel('θ'),ylabel('ρ(θ)'),title('非规则三角形的标记');

标记图中突出峰值的数量足以区分两个物体的形状。

边界线段

将边界分解为线段通常是很有用的。分解降低了边界的复杂性，从而简化了描述过程。当边界线包含一个或多个携带形状信息的明显凹度时，该方法很有用。使用由边界所围成区域的凸壳就成为边界鲁棒分解的有力工具。
集合S的凸壳H是包含S的最小凸集，集合的差H-S被称为S的凸缺D。
分段算法：追踪S的轮廓，并标记进入或离开一个凸缺的转变点，从打标记的位置进行分段。

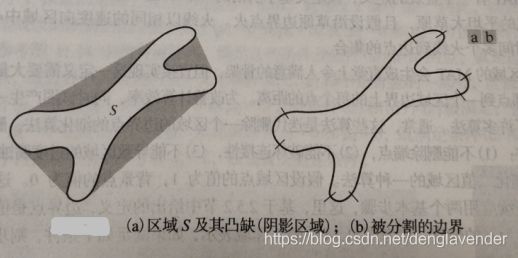
缺点：由于数字化、噪声和分割的变形的影响，导致会出现很多零碎的划分。
解决方法：先平滑边界，或进行多边形近似（更稳定），再进行分段。

骨架

表示平面内结构形状的一种重要方法是将它简化为图形。通过骨架化（细化）算法得到该区域的骨架来实现。
一个区域的骨架可以用中轴变换(MAT)来定义：R是一个区域，B为其边界，对R中的每个点p，寻找p最邻近B的点，若这样的点多于一个，则称这样的点的集合构成区域R的骨架。可以用“草原之火”来形象化：大火从边界开始以相同的速度向中心燃烧，它们集合的地方就是骨架。

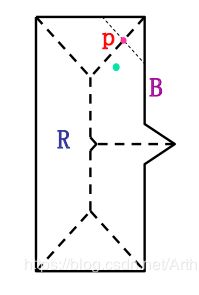
bwmorph——生成二值图像B中的所有区域的骨架（一种形态学处理方法）

S = bwmprph(B,'skel',n)
B：二值图像
'skel':对图像执行骨架操作
n：函数执行的次数，若n = Inf，则会一直重复运算，直到图像不再发生变化

在 n = Inf 时，该函数删除对象边界上的像素，但不允许对象分裂。其余的像素构成图像骨架。
示例：计算一个染色体图像的骨架

f = imread('chromo_original.tif');
f=im2double(f);  
h = fspecial('gaussian',25,15);     
g = imfilter(f,h,'replicate');          %用高斯空域模板平滑图像
g1 = imbinarize(g,1.5*graythresh(g));    %对平滑后图像进行阈值处理（将自动确定的阈值乘以1.5，以增加50%的阈值处理量，目的在于增加阈值可增加从边界中删除的数据数量，从而实现进一步平滑）

s = bwmorph(g1,'skel',Inf);   % 提取骨架
s1 = bwmorph(s,'spur',8);  % 删除骨架中的毛刺
s2 = bwmorph(s1,'spur',7);

figure;
subplot(2,3,1); imshow(f);title('原图');
subplot(2,3,2); imshow(g); title('用高斯空域模板平滑原图');
subplot(2,3,3); imshow(g1); title('对平滑后的图像进行阈值处理');
subplot(2,3,4); imshow(s); title('骨架图像');
subplot(2,3,5); imshow(s1); title('对骨架图像8次删除毛刺得到的图像');
subplot(2,3,6); imshow(s2); title('再删除7次毛刺得到的图像');

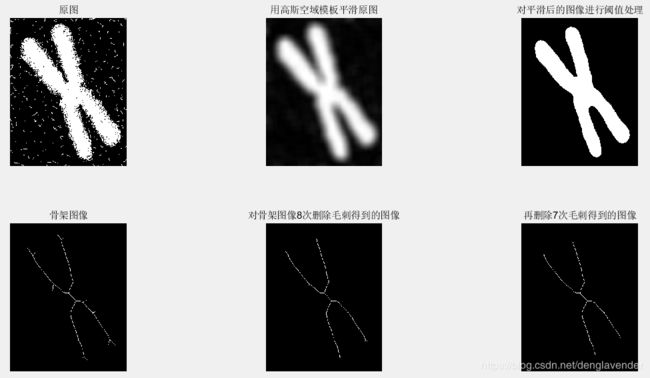
我们的目的是计算染色体的骨架，因此第一步是将染色体与背景无关的细节加以分离，即对图像进行平滑处理，然后对其进行阈值处理。对自动确定的阈值乘以1.5，以增加50%的阈值处理量，从而增加从边界中删除的数据数量，实现进一步的平滑。

三、边界描绘子

一些简单的描绘子

主要介绍边界的长度（周长）、直径、偏心率、曲率四种描绘子。
边界的长度是最简单的描绘子之一。
4连接边界的长度仅是边界中的像素数减1；8连接边界的长度，垂直和水平平移记为1，对角平移记为√2。
函数bwperim——获得二值图像中对象的周长

g = bwperim(f, conn)
f：二值图像
conn：边界连接性，4或8（默认）
g：包含f中的对象的边界的二值图像

边界B的直径定义：

其中D为距离测度，一般使用欧氏距离。p_i和p_j为边界B上的点。即边界尚两个最远点间的欧氏距离。
边界上的最远点并不总是唯一，如圆和方形上的点。但通常会假设：直径是一个有用的描绘子，则最好应用到具有单个最远点对的边界。
连接边界最远点对的线段称为边界的长轴。边界短轴定义为与长轴垂直的线段。长轴和短轴所形成的矩形完全包含了边界，该矩形称为基本矩形。长轴和短轴的比率是边界的偏心率。
偏心率也是一个有用的描绘子。
曲率：定义为斜率的变化率。近似：用相邻边界线段的斜率差作为这两条线段交点处的曲率。
自定义函数diameter——计算边界的直径、长轴、短轴和边界或区域的基本矩形

s = diameter(L)
L：标记矩阵，可使用bwlabel函数获得
s是一个结构体，包含如下域：
s.Diameter ：标量，边界或区域中任意两个像素之间的最大距离（直径）。
s.MajorAxis：2*2矩阵，其中的行包含边界或区域的长轴端点的行、列坐标。
s.MimorAxis：2*2矩阵，其中的行包含边界或区域的短轴端点的行、列坐标。
s.BasicRectangle ：4*2矩阵，其中的每行包含基本矩阵的一个角的行、列坐标。

形状数

边界的形状数一般是以4连接的佛雷曼链码为基础的，形状数被定义为最小值整数序列的一阶差分，形状数的阶n定义为表示形状数的数字的个数。 边界的形状数可以用函数fchcode中的c.diffmm给出，形状数的阶n使用length(c.diffmm)得到。对于闭合边界，n为偶数。

傅里叶描绘子

对xy平面内的一个K点数字边界。从任意点(x₀,y₀)开始，以逆时针方向熵在该边界上行进时，会遇到坐标对(x₀,y₀)，(x₁,y₁)，(x₂,y₂)，…(x_K-1,y_K-1)。这些坐标可以表示为x(k) = x_k,y(k) = y_k的形式。

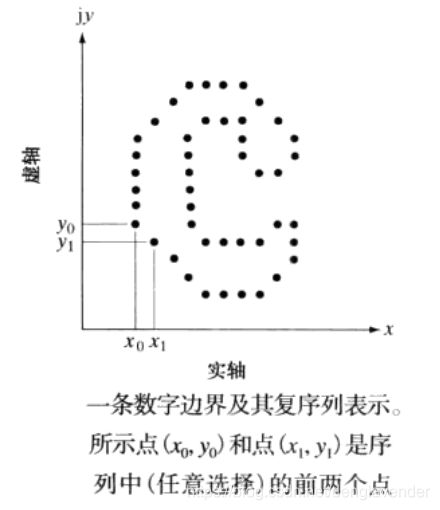
故边界可以表示为坐标序列s(k) = [x(k),y(k)]，其中k = 0,1,2,…，K-1。坐标也可以当作一个复数，即

其中k = 0,1,2,…，K-1。尽管对该序列的解释是全新的，但边界本身的性质并未改变，这种表示方法将二维问题转换为一维。
s(k)的离散傅里叶变换（DFT）为

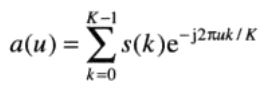
其中u = 0,1,2,…，K-1。其中复系数a(u)称为边界的傅里叶描绘子。这些系数的傅里叶反变换可恢复s(k)：

其中k = 0,1,2,…，K-1。若使用前P个傅里叶系数而不是所有系数来恢复s(k)，即当u>P-1时，令a(u) = 0。故s(k)的近似为：

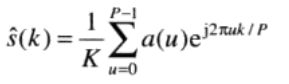
其中k = 0,1,2,…，K-1。尽管只使用了P项进行恢复，但k的范围仍是从0~K-1。即近似边界中包含有相同数量的点，但每个点的重构中却用不到如此多的系数项。回忆可知，高频分量决定细节部分，低频分量决定总体形状。故P越小，边界丢失的细节就越多。

自定义函数frdescp——计算边界的傅里叶描绘子

z = frdescp(s)
s：是一个np*2数组，描述图像中对象的边界坐标

自定义函数ifrdescp——用给定数量的描绘子计算其逆变换

s = ifrdescp(z,nd)
z：傅里叶描绘子
nd：描绘子的数量

示例：傅里叶描绘子

f = imread('chromo_original.tif');
f=im2double(f);
h=fspecial('gaussian',15,9);
g=imfilter(f,h,'replicate');
g=imbinarize(g,0.7);    %变成二值图像。使用上面的参数对图像进行处理，目的是产生一幅并不完全光滑的图像，以便用它来说明减少描绘子的数量对边界形状产生的影响。
[M,N] = size(f);
b=boundaries(g);  % 得到边界坐标，有1090个像素点
b=b{1};
bim=bound2im(b,M,N);    

z=frdescp(b); %用边界坐标b进行傅里叶变换系数(有多少个点就有多少个系数)，将b的坐标点看成是复平面中的某个复数
z546=ifrdescp(z,546); %用50%的描绘子进行逆变换
z546im=bound2im(z546,M,N);

z110=ifrdescp(z,110); %用10%的描绘子进行逆变换
z110im=bound2im(z110,M,N);

z56=ifrdescp(z,56); %用5%的描绘子进行逆变换
z56im=bound2im(z56,M,N);

z28=ifrdescp(z,28); %用2.5%的描绘子进行逆变换
z28im=bound2im(z28,M,N);

z14=ifrdescp(z,14); %用1.25%的描绘子进行逆变换
z14im=bound2im(z14,M,N);

z8=ifrdescp(z,8); %用0.70%的描绘子进行逆变换
z8im=bound2im(z8,M,N);

figure;
subplot(3,3,1),imshow(f),title('原始图像');
subplot(3,3,2),imshow(g),title('阈值处理后');
subplot(3,3,3),imshow(bim),title('提取的边界图');
subplot(3,3,4),imshow(z546im),title('546个描绘子恢复后的边界');
subplot(3,3,5),imshow(z110im),title('110个描绘子恢复后的边界'); 
subplot(3,3,6),imshow(z56im),title('56个描绘子恢复后的边界');
subplot(3,3,7),imshow(z28im),title('28个描绘子恢复后的边界');
subplot(3,3,8),imshow(z14im),title('14个描绘子恢复后的边界');
subplot(3,3,9),imshow(z8im),title('8个描绘子恢复后的边界');

原始边界由1090个点组成，也就是说对应的傅里叶描绘子有1090个。由图可知，14个描绘子就有效的保持了原始边界的主要形状特征，但8个描绘子恢复的结果是不可接受的。
如前所述，描绘子应尽可能对平移、旋转和尺度变换不敏感。在所得结果依赖于点被处理的顺序时，要加一个额外约束是，描绘子应对起始点不敏感。傅里叶描绘子并非直接对这些几何变化不敏感，但这些参数的变化可能与描绘子的简单变换是相关的。

统计矩

边界线段（和标记图波形）的形状可使用统计矩来定量描述，如均值、方差和高阶矩。

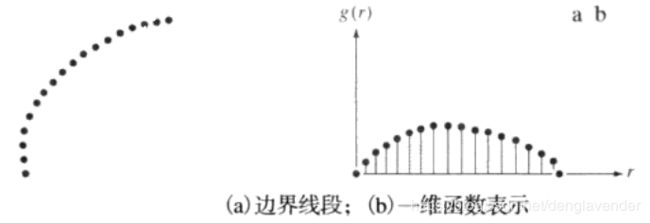
上图(a)显示了一个边界线段，图(b)显示了一个以任意变量r的一维函数g®描绘的线段。该函数是这样获得的：先将该线段的两个端点连接起来，然后旋转该直线线段，直到该直线线段称为水平线段。此时，边界线段上的所有点的坐标也旋转相同的角度。
描述g®的形状的一种方法是将g®归一化到单位面积内，并把它当做一个直方图来处理。g(r_i)作为r_i出现的概率。故r可看作一个随机变量，其矩为

其中，m的表达式如下：

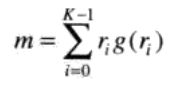
其中K是边界上的点数，μ_n（r）直接与g（r）的形状相关。
在文献中n阶矩通常用符号μ_n表示，直接使用变量计算的矩被称为原始矩（raw moment），移除均值后计算的矩被称为中心矩（central moment）。变量的一阶原始矩等价于数学期望（expectation）、二至四阶中心矩被定义为方差（variance，度量曲线关于r的均值的扩展程度）、偏度（skewness，度量曲线关于均值的对称性）和峰度（kurtosis）。

statmomemts——计算n阶中心矩，并返回行向量v。
因为0阶矩总为1,1阶矩总为0，故忽略这两个矩。令v(1) = m，v(k) = μ_k，k = 2,3，…，n

[v,unv] = statmoments(p,n)
p：直方图向量。要求对于unit8类图像，p的分量数等于2^8^；对于uint16类图像，p的分量数等于2^16^；对于double类图像，p的分量数等于2^8^或2^16^
n：计算的矩的数量
v：向量v包含了以随机变量值为基础的归一化矩，而随机变量已被标度在区间[0,1]内，故所有的矩也在这个区间内。即v(1)表示均值，v(2)表示方差，等等
nuv：向量unv包含了与v相同的矩，但用位于原始值区间内的数值计算。

示例：statmoments函数的简单使用（主要是想记录一下怎么求参数p）

f = imread('building.tif');
imshow(f);
p = imhist(f);
p = p./numel(f);
[v,nuv] = statmoments(p, 3);  

其中的v和nuv如下

>> v
v =
    0.5992    0.0677   -0.0091
>> nuv
nuv =
   1.0e+05 *
    0.0015    0.0440   -1.5118

四、区域描绘子

使用边界和区域相结合的描绘子在实践中是很普遍的。

一些简单的描绘子

主要介绍区域的面积、周长、致密性、圆度率、及其他简单测度。
1、面积
区域中像素的数量。
2、周长
区域边界的长度。
3、致密性
（周长）²/面积
4、圆度率
一个区域的面积与具有相同周长的圆(最致密形状)的面积之比。周长为P的一个圆的面积为P²/4π。故圆度率R_c如下

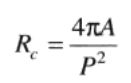
A是所讨论区域的面积，P是其周长。对于圆形区域，圆度率为1，对于方形区域，圆度率为π/4。
5、其他
用作区域描绘子的其他简单测度包括灰度级的均值和中值、最小灰度值和最大灰度值，以及其值高于和低于均值的像素数。

函数regionprops是用于计算区域描绘子的主要工具。

D = regionprops(L,properties)
L：是一个标记矩阵，L中不同的正整数元素对应不同的区域。可通过bwlabel函数获得。例如：L中等于整数1的元素对应区域1；L中等于整数2的元素对应区域2；以此类推。
properties：可以是一个用逗号分隔的字符串列表、一个包含字符串的元胞数组、单个字符串'all'或字符串'basic'。若properties是'all'，则将计算下表所示的所有描绘子；若未指定properties或是指定为字符串'basic'，则仅计算'Area'、'Centroid'、'BoundingBox'。
D：是一个长度为max((L:))的结构体。该结构体的域表示每个区域的不同度量，就像properties指定的那样。

x和y分别表示水平和垂直坐标，原地定于左上角。x轴和y轴分别从原点开始沿着向右和向下的方向增长。on像素的值为1，off像素的值为0.

properties的有效字符串	解释说明
‘Area’	图像中各个区域内的像素总数
‘BoundingBox’	包含区域的最小矩形，1*4向量：[矩形左上角x坐标，矩形左上角y坐标，x方向长度，y方向长度]
‘Centroid’	每个区域的质心，1*2向量。[质心x坐标，质心y坐标]
‘ConvexArea’	标量，‘ConvexImage’中的像素数
‘ConvexHull’	包含区域的最小凸多边形， p*2矩阵。矩阵的每一行包含多边形的p个顶点之一的x和y坐标。
‘ConvexImage’	画出上述区域的最小凸多边形，二值图像，凸壳
‘Eccentricity’	标量，与区域有着相同二阶矩中心矩的椭圆的偏心率（离心率）。偏心率是椭圆的焦距与主轴长度间距离的比率。其值在0和1之间，等于0和1是退化的情况（偏心率为0的椭圆是圆，偏心率为1的椭圆是线段）
‘EquivDiameter’	标量，与区域有着相同面积的圆的直径。计算为sqrt(4*Area/pi)
‘EulerNumber’	标量，欧拉数，等于区域中的对象数减去这些对象中的孔洞数
‘Extent’	标量，同时在区域和其最小边界矩形中的像素的比例。计算为：Area/最小边界矩形的面积
‘Extrema’	8*2的矩阵，8邻接区域中的极值点
‘FilledArea’	FilledImage中on像素的数目
‘FilledImage’	与某区域具有相同大小的二值图像。on像素对应于所有孔洞均已填充的区域
‘Image’	与某区域具有相同大小的二值图像。on像素对应于该区域，其他像素为off像素
‘MajorAxisLength’	与区域有着相同二阶矩中心矩的椭圆的长轴长度（像素意义下）
‘MinorAxisLength’	与区域有着相同二阶矩中心矩的椭圆的短轴长度（像素意义下）
‘Orientation’	x轴和与区域有着相同二阶矩中心矩的椭圆的长轴间的角度（单位为度）
‘PixelList’	行为区域内实际像素的[x,y]坐标的矩阵
‘Solidity’	标量，同时在区域和其最小凸多边形中的像素的比例。计算为：Area/ConvexArea

示例：regionprops函数的简单实用。

f = imread('mapleleaf.tif');
imshow(f);
L = bwlabel(f);
A = regionprops(L,'area','centroid','boundingbox');
B = [A.Area];  % 不同区域的面积
NR = numel(B);  % 图像中的区域个数
C = A.Centroid; % 每个区域对应的质心
V = A.BoundingBox;  % 包含区域的最小矩形

>> A
A = 
  包含以下字段的 struct:
           Area: 37215
       Centroid: [149.9109 145.5666]
    BoundingBox: [13.5000 8.5000 270 297]
>> B = [A.Area]
B =
       37215
>> NR = numel(B)
NR =
     1
>> C = A.Centroid
C =
  149.9109  145.5666
>> V = A.BoundingBox
V =
   13.5000    8.5000  270.0000  297.0000

拓扑描绘子

拓扑特性对于图像平面区域的整体描述很有用。拓扑学研究未受任何变形影响的图形的性质，前提是该图形未被撕裂或粘连。
如果一个拓扑描绘子由该区域内的孔洞数量来定义，那么这种性质明显不受拉伸或旋转变换的影响。拓扑特性与距离或基于距离测度概念的任何特性无关。
另一个对区域描述有用的拓扑特性是连通分量的数量。

图形中孔洞的数量 H 和连通分量的数量 C ，可用于定义欧拉数 E ：E = C - H

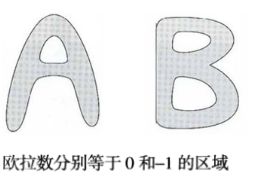
A：一个连通分量一个空洞，B：一个连通分量两个空洞
使用欧拉数，可以很简单地解释由直线线段表示的区域（多边形网络）。
V-Q+F= C-H = E
其中V表示顶点数，Q是边数，F是面数。

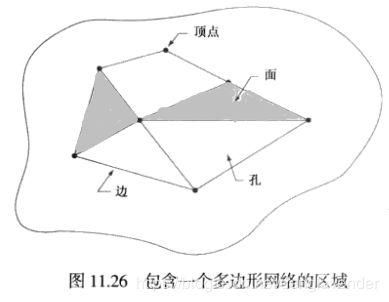
上图的欧拉数：7 - 11 + 2 = 1 - 3 = -2。

纹理

描绘区域的一种重要方法是量化该区域的纹理内容。图像处理中用于描绘区域纹理的三种主要方法是统计法、结构法和频谱法。
统计法：获得诸如平滑、粗糙、粒状等纹理特征。
结构法：处理图像像元的排列，如基于规则间距平行线的纹理描述。
频谱法：基于傅里叶频谱的特性，主要用于检测图像中的全局周期性，方法是识别频谱中的高能量的窄波峰。

• 统计法

该方法是基于灰度直方图的统计特性。令z表示灰度的一个随机变量，令p(z_i)，i = 0,1,2,…，L-1为相应的直方图，L为不同灰度级的数量。关于均值的z的第n阶矩为：

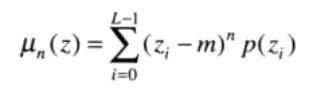
其中，m是z的均值（平均灰度）：

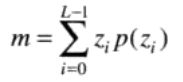
其中，μ₀ = 1，μ₁ = 0。二阶矩μ₂(z)为方差σ²。

四阶矩是直方图相对平坦度的测度。
自定义函数statxture——计算上表中的六种纹理度量

t = statxture(f,scale)
f：一幅输入图像（或子图像）
t：是一个6元素行向量，其分量是上述六种纹理描绘子。这些描绘子都以相同的顺序排列。
scale：一个6元素行向量，为达到缩放的目的，它的元素要与t的相应元素相乘。若省略，则scale的默认值都是1

示例：统计纹理度量

f1 = imread('superconductor-with-window.tif');
f2 = imread('cholesterol-with-window.tif');
f3 = imread('microporcessor-with-window.tif');
subplot(131),imshow(f1),title('平滑纹理图');
subplot(132),imshow(f2),title('粗糙纹理图');
subplot(133),imshow(f3),title('规则纹理图');
t1 = statxture(f1);  %统计纹理的度量
t2 = statxture(f2);  
t3 = statxture(f3);  
subplot(131),imhist(f1),title('平滑纹理图直方图');
subplot(132),imhist(f2),title('粗糙纹理图直方图');
subplot(133),imhist(f3),title('规则纹理图直方图');

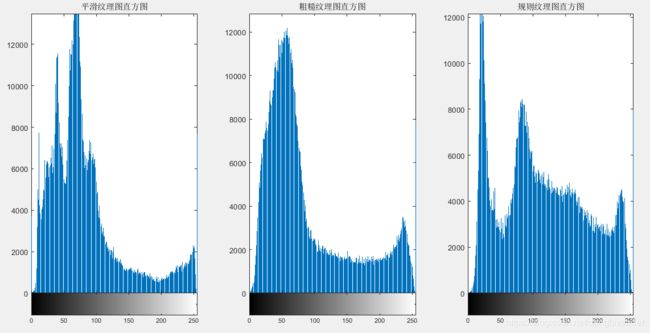
注意：这里是处理整幅图像的结果，而不是局部图像（白框包围的区域）

>> t1
t1 =
   83.1067   56.9098    0.0474    4.0500    0.0079    7.3638
>> t2
t2 =
   89.6103   66.6801    0.0640    5.0331    0.0071    7.4994
>> t3
t3 =
  115.0471   67.4126    0.0653    1.3080    0.0051    7.7887

仅使用直方图计算得到的纹理测度不携带像素彼此间的相对位置信息，但在描述纹理时，这些很重要。因此引入灰度共生矩阵。这种方法不仅考虑灰度的分布，还考虑图像中像素的相对位置。
灰度共生矩阵的生成方式：令Q是定义两个像素彼此相对位置的一个算子，并考虑一幅具有L个可能灰度级的图像f，令G为一个矩阵，其元素g_ij是灰度为z_i 和z_j的像素对出现在f中由Q所指定的位置处的次数，其中1 <= i,j<=L。按照这种方法形成的矩阵称为灰度共生矩阵

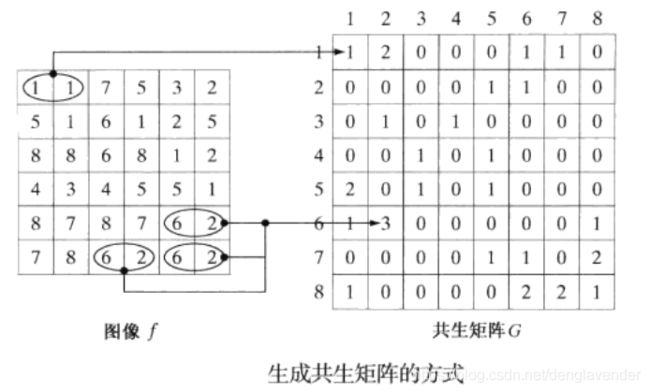
通俗来讲就是：找到图像f中可能的灰度级数L，生成一个L*L 的矩阵G，矩阵中的元素是看其行号和列号在图像f中有没有Q指定的相对位置，出现几次，该位置就是几。如矩阵G的（6,2）位置，对应的图像像素出现了三次（像图中圈出的那样），则该位置的值为3，其余的类似。

满足Q的像素对的总数n，等于G的元素之和。故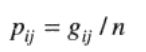
是满足Q的一个值为(z_i,z_j)的点对的概率估计。这些概率的值域为[0,1]，且它们的和为1

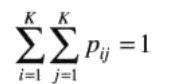
K为方阵G的行数（或列数）。

其中

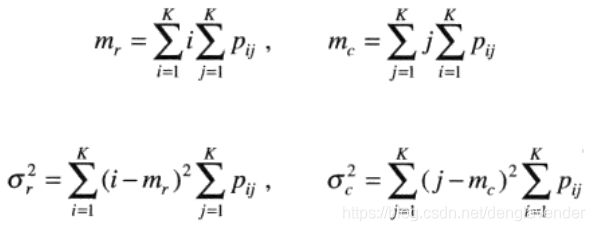
m_r是沿归一化后的G的行计算的均值，m_c是沿归一化后的G的行计算的均值；
σ_r和σ_c是分别沿行和列计算的标准差。
函数graycomatrix——从图像创建灰度共生矩阵。调用格式如下

glcms = graycomatrix(I)
或 glcms = graycomatrix(I,Name,Value,...)
或 [glcms,SI] = graycomatrix(I,Name,Value,...)
I：输入图像
名称-值对参数
  'GrayLimits'：将输入图像缩放到灰度级所使用的范围(指定缩放的方式)
      为二元向量[low high]。如果 N 是用于缩放的灰度级的数量（参见NumLevels），小于或等于 low 的灰度值将缩放为 1。大于或等于 high 的灰度值将缩放至 'NumLevels'。如果参数设为[]，则共生矩阵使用图像的最小和最大灰度值作为界限，即[min(I(:)) max(I(:))]。
  'NumLevels'：整数，说明I中进行灰度缩放的灰度级数目。
     如果NumLevel设为8，则 graycomatrix 将 I 中的值缩放为 1 到 8 之间的整数。灰度级的数目决定了共生矩阵glcm的尺寸。缺省情况：数字图像：8；二进制图像：2。
  'Offset'：关注的像素与其邻点之间的距离
      指定为由整数组成的 p×2 数组。数组中的每行均为一个二元素向量，即 [row_offset, col_offset]，它指定一对像素的关系（即偏移量）。row_offset 是关注的像素与其邻点之间的间隔行数。col_offset 是关注的像素与其邻点之间的间隔列数。默认为[0 1]。
      移常表达为一个角度，常用的角度如下：（其中D为像素距离） 
		角度 0 45 90 135 
		Offset [0,D] [-D D] [-D 0] [-D -D]
  'Symmetric'：考虑值的顺序
  	  指定为布尔值 true 或 false。设置为 true 时创建的 GLCM 是关于其对角线对称的。例如，当 'Symmetric' 设置为 true 时，graycomatrix 在计算值 1 与值 2 相邻的次数时，会将 1,2 和 2,1 对组都进行计数。当 'Symmetric' 设置为 false 时，graycomatrix 根据 'offset' 的值仅对 1,2 或 2,1 进行计数。
glcms：灰度共生矩阵
SI ： 用于 GLCM 计算的缩放图像

示例：graycomatrix函数的简单应用

>> I = [ 1 1 5 6 8 8; 2 3 5 7 0 2; 0 2 3 5 6 7];
[glcm,SI] = graycomatrix(I,'NumLevels',9,'GrayLimits',[3 7]);
>> I
I =
     1     1     5     6     8     8
     2     3     5     7     0     2
     0     2     3     5     6     7
>> SI
SI =
     1     1     5     7     9     9
     1     1     5     9     1     1
     1     1     1     5     7     9
>> glcm
glcm =
     5     0     0     0     3     0     0     0     0
     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     2     0     1
     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     2
     0     0     0     0     0     0     0     0     0
     1     0     0     0     0     0     0     0     1

函数graycoprops——用于产生灰度共生矩阵特性的描绘子

stats = graycoprops(glcm,properties)
glcm：灰度共生矩阵，可以是一个，也可以是多个（在指定多个'Offset'的情况下），多个glcm的时候，stats会统计每个glcm的统计信息。该函数会自动将glcm归一化。
properties：灰度共生矩阵的属性，即描绘子。主要有以下几种属性：（具体的上面的表中有说明）
    'Contrast'：对比度
    'Correlation'：相关
    'Energy'：能量（一致性）
    'Homogeneity'：同质性
    若不指定properties，则会返回所有的属性的统计信息
stats：指定属性中的统计信息。是一个结构体。

示例：使用描绘子表征灰度共生矩阵

f1 = imread('random_matches.tif');
f2 = imread('ordered_matches.tif');
f3 = imread('microporcessor-with-window.tif');
figure;
subplot(1,3,1),imshow(f1),title('随机模式图');
subplot(1,3,2),imshow(f2),title('有序模式图');
subplot(1,3,3),imshow(f3),title('混合模式图');

G1 = graycomatrix(f1,'NumLevels',256);  % 生成灰度共生矩阵
G2 = graycomatrix(f2,'NumLevels',256);   
G3 = graycomatrix(f3,'NumLevels',256); 

G1n = G1/sum(G1(:));  % 对灰度共生矩阵进行归一化，是为了最大概率和熵的计算做准备
G2n = G2/sum(G2(:));
G3n = G3/sum(G3(:));

stats1 = graycoprops(G1);  % 从灰度共生矩阵中提取描绘子
stats2 = graycoprops(G2);
stats3 = graycoprops(G3);

maxProbability1 = max(G1n(:));   %最大概率
maxProbability2 = max(G2n(:));   
maxProbability3 = max(G3n(:));   

for I = 1:size(G1n,1)
sumcols(I) = sum(-G1n(I,1:end).*log2(G1n(I,1:end)+eps));
end
entropy1 = sum(sumcols);   %熵

for I = 1:size(G2n,1)
sumcols(I) = sum(-G2n(I,1:end).*log2(G2n(I,1:end)+eps));
end
entropy2 = sum(sumcols);   

for I = 1:size(G3n,1)
sumcols(I) = sum(-G3n(I,1:end).*log2(G3n(I,1:end)+eps));
end
entropy3 = sum(sumcols); 

三个图像共生矩阵的描绘子如下：

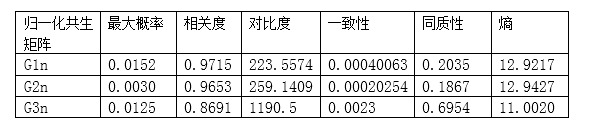
图像的随机性（熵）越低，对比度往往也越低。
图像中的随机性越低，一致性描绘子就越高。

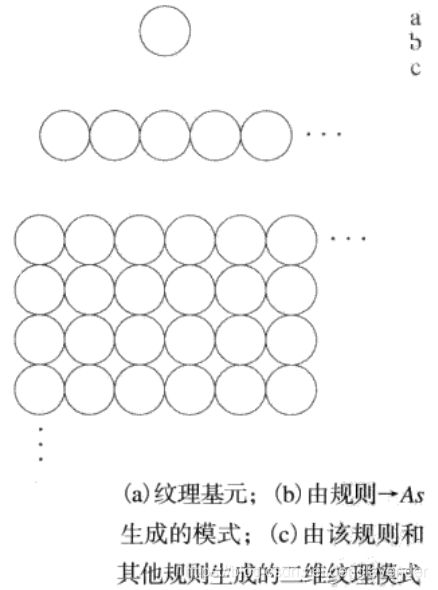
• 结构法

一个简单的“纹理基元”可以借助一些规则用于形成更复杂的纹理模式，这些规则限制基元（或这些基元）的可能排列的数量。

• 频谱法

傅里叶频谱非常适合描述图像中的二维周期或近似二维周期模式的方向性。纹理的频谱对于判别周期纹理模式和非周期纹理模式非常有用，对量化两个周期模式间的差也非常有用。
对纹理描述很有用的傅里叶频谱的三个特征：
（1）频谱中突出的尖峰给出纹理模式的主要方向；
（2）频率平面中尖峰的位置给出模式的基本空间周期；
（3）采用滤波方法消除任何周期成分而留下非周期性图像元素，然后采用统计技术来描述。
频谱是关于原点对称的，故只要考虑半个频率平面。
使用极坐标表示频谱所得到的函数S(r,θ)可以频谱特性的解释：S是频谱函数，r和θ是极坐标系中的变量。对每个方向θ，S(r,θ)视为一个一维函数S_θ®。类似的，对每个频率r，S_r(θ)也是一个一维函数。对固定值θ分析S_θ®，可得到从原点出发沿半径方向的频谱特性，对固定值r分析S_r(θ)，可得到以原点为圆心的一个圆上的频谱特性。
对两个一维函数进行积分（对离散变量求和），可得到整体描述：

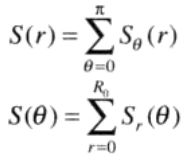
其中R₀为以原点为圆心的圆的半径。
为定量表征特性，可计算S®和S(θ)本身的描绘子，典型的描绘子是最高值的位置、幅度和轴向变化的均值与方差，以及该函数的均值和最高值之间的距离。

自定义函数specxture——计算S®和S(θ)两个纹理度量。

[srad,sang,S] = specxture(f)
srad：是S(r)
sang：是S(θ)
S：是频谱图

示例：频谱纹理

f1 = imread('random_matches.tif');
f2 = imread('ordered_matches.tif');
[srad1,sang1,S1] = specxture(f1);  
[srad2,sang2,S2] = specxture(f2);  

figure;subplot(2,2,1),imshow(f1),title('随机火柴的图像');
subplot(2,2,2),imshow(f2),title('整齐排列的火柴图像');
subplot(2,2,3),imshow(S1),title('随机火柴的频谱图像');
subplot(2,2,4),imshow(S2),title('整齐火柴的频谱图像');

figure;subplot(2,2,1),plot(srad1),xlabel('r'),ylabel('S(r)'),title('随机火柴S(r)图像');
subplot(2,2,2),plot(sang1),xlabel('θ'),ylabel('S(θ)'),title('随机火柴S(θ)图像');
subplot(2,2,3),plot(srad2),xlabel('r'),ylabel('S(r)'),title('整齐火柴S(r)图像');
subplot(2,2,4),plot(sang2),xlabel('θ'),ylabel('S(θ)'),title('整齐火柴S(θ)图像');

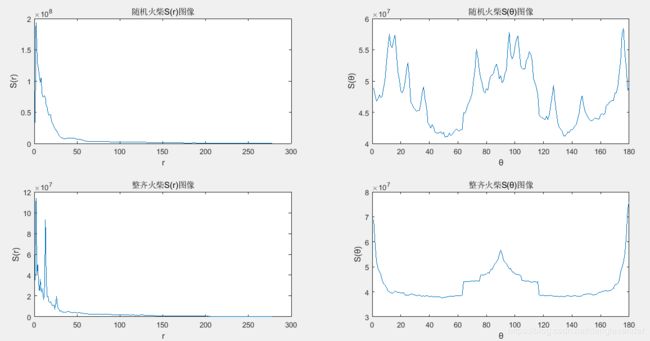
由于粗糙背景材质上火柴的摆放形成了周期纹理，所以在二维傅里叶频谱中出现了向四周扩展的周期突变。
随机火柴图像频谱中的其他成分是由图像中任意排列的强边缘产生的，而整齐火柴频谱的能量主要集中在水平轴方向，对应与火柴摆放的垂直边缘。
随机火柴的S®曲线无很强的周期分量（即在频谱中除了原点处有一个峰值外，没有其他峰值），S(θ)的能量脉冲的随机性也很明显；整齐火柴的S®曲线在r = 15处有一个强峰值，在r = 25处也有一个小峰值，S(θ)曲线表明在原点附近的区域中以及在θ = 90°和θ = 180°处有较强的能量分量。

不变矩

大小为M*N的数字图像f(x.y)的二维(p + q)阶矩定义为

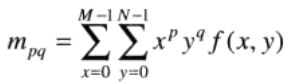
p和q均为0,1,2,…的整数。相应的(p + q)阶中心矩定义为

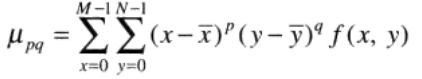
其中

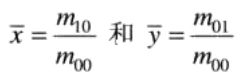
归一化的中心矩定义为

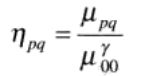
其中

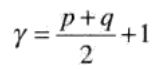
p + q = 2,3,…
由二阶矩和三阶矩可推出如下7个不变矩组：

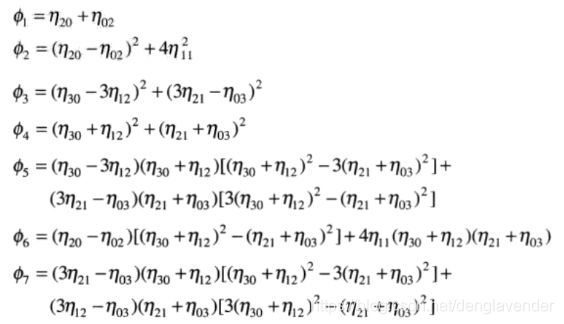
以上7个不变矩对于平移、尺度变化、镜像（内部为负号）和旋转是不变的。
自定义函数invmoments可用来计算上述7个不变矩

phi = invmoments(f);  %f是输入图像，phi是包含不变矩7个元素的行向量 

示例

f = imread('Original_Padded.tif');

fp = padarray(f,[84 84],'both');    % 填充过的原始图像,填充不影响不变矩的计算

ftrans = zeros(568,568,'uint8');    
ftrans(151:550,151:550) = f;     % 平移过的图像

fhs = f(1:2:end,1:2:end);
fhsp = padarray(fhs,[184 184],'both');     % 拥有一半尺寸且对应的填充图像

fm = fliplr(f); %获取镜像图像
fmp = padarray(fm,[84 84],'both');   % 填充镜像图像  

    % 使用imrotate可以旋转图像，调用格式如下：
    % g = imrotate(f,angle,method,'crop')
    % 该函数逆时针旋转图像angle度。参数method可以是'nearest'（最邻近插值方法，默认）、'bilinear'（线性插值方法，典型选择）、
    %'bicubic'（双三次插值方法），若参数中包含'crop'，则旋转后的图像的中心部分会被修建为与原图像相同的尺寸。
fr45 = imrotate(f,45,'bilinear');    %旋转45°线性内插后的图像
fr90 = imrotate(f,90,'bilinear');   %旋转90°线性内插后的图像

fr90p = padarray(fr90,[84 84],'both');   %对旋转90°图像进行填充

phif = invmoments(f);  % 原始图像的不变矩
phiftrans = invmoments(ftrans);  % 平移图像的不变矩
phifhsp = invmoments(fhsp);  % 填充一半尺寸图像的不变矩
phifmp = invmoments(fmp);  % 镜像图像的不变矩
phifr45 = invmoments(fr45);  % 旋转45°图像的不变矩
phifr90 = invmoments(fr90);  % 旋转90°图像的不变矩

subplot(2,4,1),imshow(f),title('原始图像');
subplot(2,4,2),imshow(fp),title('填充原始图像');
subplot(2,4,3),imshow(ftrans),title('平移原始图像');
subplot(2,4,4),imshow(fhsp),title('填充一半尺寸的图像');
subplot(2,4,5),imshow(fmp),title('镜像图像');
subplot(2,4,6),imshow(fr45),title('旋转45°线性内插后的图像');
subplot(2,4,7),imshow(fr90),title('旋转90°线性内插后的图像');
subplot(2,4,8),imshow(fr90p),title('旋转90°线性内插后并填充的图像');

format short g   
phi_norm = -sign(phi).*(log10(abs(phi)))     % 使用log10变换减少它们的动态范围
phiftrans_norm = -sign(phiftrans).*(log10(abs(phiftrans)))
phifhsp_norm = -sign(phifhsp).*(log10(abs(phifhsp)))
phifmp_norm = -sign(phifmp).*(log10(abs(phifmp)))
phifr45_norm = -sign(phifr45).*(log10(abs(phifr45)))
phifr90_norm = -sign(phifr90).*(log10(abs(phifr90)))

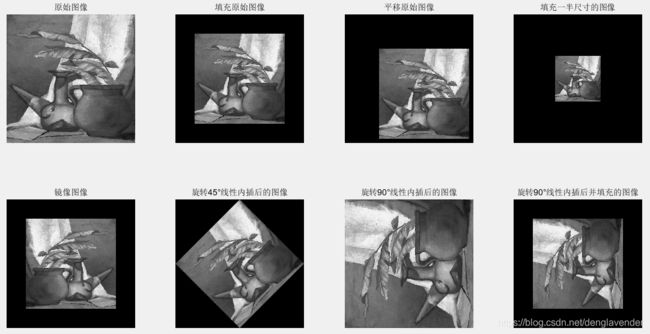
各幅图像的不变矩

从表中可以看出矩的值都很接近，与平移、尺度缩放、镜像和旋转无关；ϕ₇的符号对于镜像图像是不同的（这是实践中用于检测一幅图像是否已被镜像的一种性质）

五、使用主成分进行描绘

本节内容适用于边界和区域。也是描绘一组空间上已配准图像的基础。
主成分变换，是指由原始图像数据协方差矩阵的特征值和特征向量建立起来的变换核，将光谱特征空间原始数据向量投影到平行于地物集群椭球体各结构轴的主成分方向，突出和保留主要地物类别信息，用来进行图像增强、特征选择和图像压缩的处理方法。
假设有n幅已配准的图像，他们堆叠在一起。如下图所示
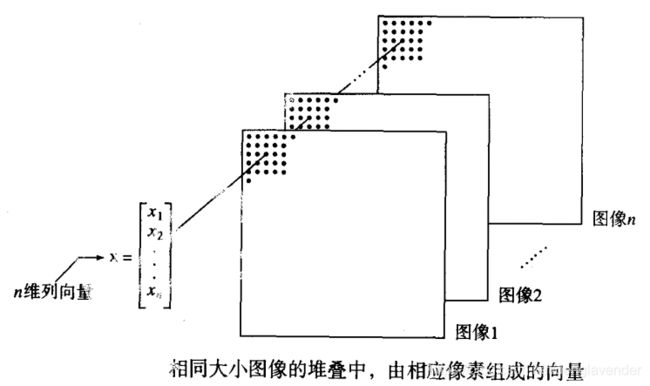对任意给定的坐标(i,j)，都有n个像素，每一幅图像在该位置上都有一个像素。这些像素以列向量的形式排列：

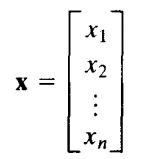
若每个图像的大小都为MN，则在n幅图像中，包含所有图像的n维向量共有MN个，即图像的个数决定向量的维数，图像的大小决定向量的个数
K（K = MN）个向量的均值向量m_x可通过样本的平均值来近似：

类似的，K个向量的nn协方差矩阵C_x可由如下式子来近似：

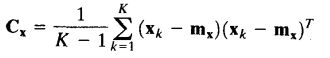
为了从样本中获得C_x的无偏估计，用K-1代替K。因为C_x是一个实对称矩阵，故总可以找到n个正交特征向量。
主分量变换（霍特林变换）如下：

A是由C_x的特征向量组成，特征向量的排序方式为A的第一行对应于最大特征值的特征向量，最后一行对应于最小特征值的特征向量。
y的均值m_y为零。
y的元素是不相关的，故y的协方差矩阵C_y是对角阵。主对角线元素就是C_x的特征值。故C_x和C_y有相同的特征值。
因为矩阵A的行向量是正交的，故A^-1 = A^T。任何向量x都能通过下式由其对应的y来恢复：

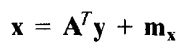
然而往往不使用C_x的所有特征向量，而是有对应的前k个最大特征值的k个特征x向量来形成矩阵A_k，得到一个k*n的变换矩阵，向量y成为k维矩阵。这就是主成分变换的魅力所在。
由A_k重建的向量x（是样本x是近似）由下式表示

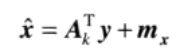
近似的x和原始x的均方误差定义如下：

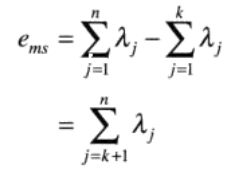
λ_j为C_x的特征值。若k = n，则误差为零，通过选取与最大特征值相对应的k个特征向量，可以使误差最小。主成分变换是最佳的。

一组n幅已配准的图像（每幅图像的大小均为M*N）可通过cat函数进行堆叠

S = cat(3,f1,f2,f3,…,fn)

自定义函数imstack2vectors——将大小为MNn的图像堆叠数组转换为一个数组

[X,R] = imstack2vectors(S,MASK)
S：是一个图像堆栈
X：是从S中提取出来的向量数组。
MASK：是一幅大小为M*N的逻辑图像或数字图像，指定了用S生成X的位置非零，其余位置为零。例如，若指向在堆叠的这些图像的右上方象限使用向量，则在该象限中MASK的值为1，而其余位置的值为0。若参数中未指定MASK，则所有的图像位置将用于形成X。
R：是一个数组，该数组的行对应于用于形成X的向量的位置的二维坐标

自定义函数princomp用来实现主成分变换
示例：使用主成分描述图像

f1 = imread('WashingtonDC_Band1_512.tif');
f2 = imread('WashingtonDC_Band2_512.tif');
f3 = imread('WashingtonDC_Band3_512.tif');
f4 = imread('WashingtonDC_Band4_512.tif');
f5 = imread('WashingtonDC_Band5_512.tif');
f6 = imread('WashingtonDC_Band6_512.tif');
figure;subplot(2,3,1),imshow(f1),title('第一幅图像');
subplot(2,3,2),imshow(f2),title('第二幅图像');
subplot(2,3,3),imshow(f3),title('第三幅图像');
subplot(2,3,4),imshow(f4),title('第四幅图像');
subplot(2,3,5),imshow(f5),title('第五幅图像');
subplot(2,3,6),imshow(f6),title('第六幅图像');

S = cat(3,f1,f2,f3,f4,f5,f6);  % 将六福图像进行堆叠
[X,R] = imstack2vectors(S); % 将堆叠组织到数组中
P = princomp(X,6); % 获得6幅主成分图像

% 显示六幅主成分图像
g1 = P.Y(:,1);
g1 = reshape(g1,512,512);
figure;subplot(2,3,1),imshow(g1,[]),title('第一幅主成分图像');   %重复六次获得每幅图分量产生的结果
g2 = P.Y(:,2);
g2 = reshape(g2,512,512);
subplot(2,3,2),imshow(g2,[]),title('第二幅主成分图像');
g3 = P.Y(:,3);
g3 = reshape(g3,512,512);
subplot(2,3,3),imshow(g3,[]),title('第三幅主成分图像');
g4 = P.Y(:,4);
g4 = reshape(g4,512,512);
subplot(2,3,4),imshow(g4,[]),title('第四幅主成分图像');
g5 = P.Y(:,5);
g5 = reshape(g5,512,512);
subplot(2,3,5),imshow(g5,[]),title('第五幅主成分图像');
g6 = P.Y(:,6);
g6 = reshape(g6,512,512);
subplot(2,3,6),imshow(g6,[]),title('第六幅主成分图像');

d = diag(P.Cy);  % 返回协方差矩阵Cy，diag：返回矩阵X的主对角线上的元素，并以列向量的形式呈现
disp(d);
P1 = princomp(X,2);    %使用小一点的q值然后进行主成分重构
h1 = P1.X(:,1);
h1 = mat2gray(reshape(h1,512,512));
h2 = P1.X(:,2);
h2 = mat2gray(reshape(h2,512,512));
h3 = P1.X(:,3);
h3 = mat2gray(reshape(h3,512,512));
h4 = P1.X(:,4);
h4 = mat2gray(reshape(h4,512,512));
h5 = P1.X(:,5);
h5 = mat2gray(reshape(h5,512,512));
h6 = P1.X(:,6);
h6 = mat2gray(reshape(h6,512,512));
figure;subplot(2,3,1),imshow(h1),title('重建第一幅图像');
subplot(2,3,2),imshow(h2),title('重建第二幅图像');
subplot(2,3,3),imshow(h3),title('重建第三幅图像');
subplot(2,3,4),imshow(h4),title('重建第四幅图像');
subplot(2,3,5),imshow(h5),title('重建第五幅图像');
subplot(2,3,6),imshow(h6),title('重建第六幅图像');

D1 = im2double(f1) - h1;  % 重建图像与原图像的误差
D2 = im2double(f2) - h2;
D3 = im2double(f3) - h3;
D4 = im2double(f4) - h4;
D5 = im2double(f5) - h5;
D6 = im2double(f6) - h6;
figure;subplot(2,3,1),imshow(D1,[]),title('第一幅原图与重建图像的差异');  
subplot(2,3,2),imshow(D2,[]),title('第二幅原图与重建图像的差异');
subplot(2,3,3),imshow(D3,[]),title('第三幅原图与重建图像的差异');
subplot(2,3,4),imshow(D4,[]),title('第四幅原图与重建图像的差异');
subplot(2,3,5),imshow(D5,[]),title('第五幅原图与重建图像的差异');
subplot(2,3,6),imshow(D6,[]),title('第六幅原图与重建图像的差异');

P1.ems  % 仅由两幅主成分图像重建图像导致的均方误差

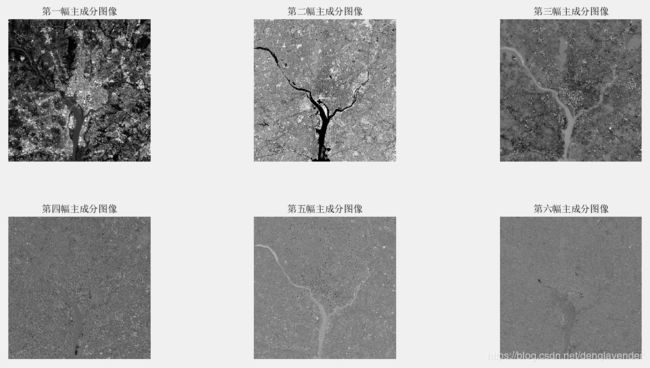
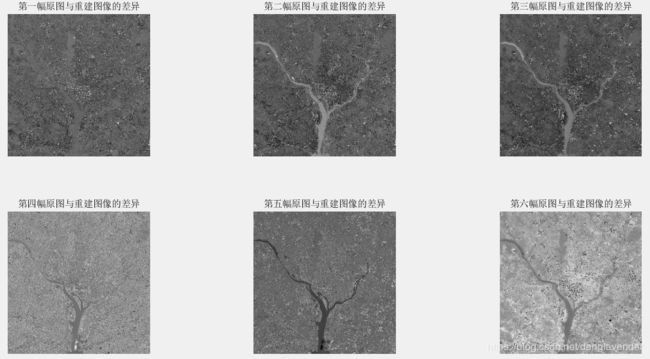
原图显示了6幅多光谱卫星图像，分别对应于6个谱带：可见蓝光，可见绿光，可见红光，近红外，中红外和热红外。
6幅图像中每幅的大小都是512*512，故一共可以构成512² = 262144个向量。主成分变换后也会产生262144个y向量。所以主成分图像第一幅就是262144个y向量的第一个分量形成的，第二幅是第二个分量形成的，以此类推。
主成分图像最明显的特征是，对比度细节的重要部分包含在前两幅图像中，并自此快速降低。从下图的特征值就能看出来，前两个特征值远大于其他特征值，因为特征值是y向量的元素的方差，而方差是灰度对比度的测度。故选择了对应于最大特征值的两幅主成分图像来重建。

重建导致的均方误差为1731.1，它是上表中λ₂到λ₆的和。
重建后的图像前五幅十分接近原图，但第六幅差异有点大，是因为原始的第六幅图像实际上是模糊的，而在重建中使用的主成分图像是清晰的，因此丢失了模糊的“细节”。

六、关系描绘子

挖掘各个成分之间的结构关系，旨在用一套模式来描述边界或区域。
图像中各个部分的连接关系是二维的，而字符串时一维结构，因此用字符串描述图像时，需要建立一种适当的方法来讲二维位置关系简化为一维形式。主导思思是从感兴趣物体中提取连接线段。

阶梯关系编码

对如下阶梯形边界，定义两个基元a，b

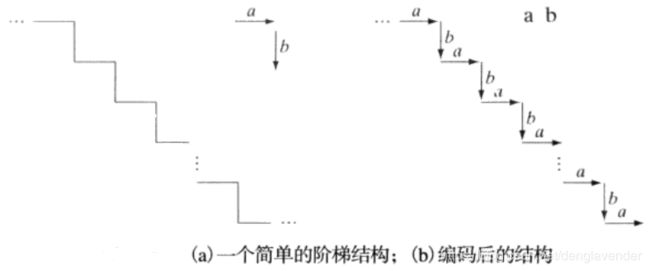
定义如下规则：S和A是变量，a和b是基元
(1) S->aA 。起始符号的S可以被基元a和变量A代替。
(2) A->bS 。变量A可以被b和S代替。
(3) A->b 。变量A只被b代替。

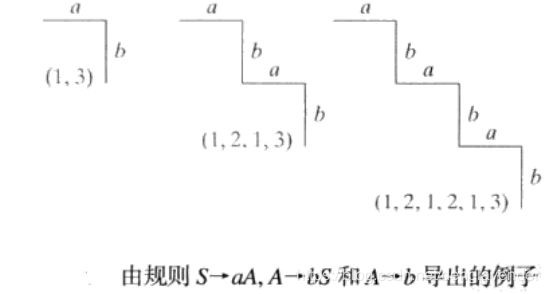
其中括号中的数字为规则的序号。

骨架关系编码

用有向线段来描述一个图像的各个部分，这个线段是通过头尾连接等方式得到的。线段之间的同运算代表了区域的不同组合。
当图像的连通性可以通过首尾相接或其他连续的方式描述时，最适于使用这种串来描述。

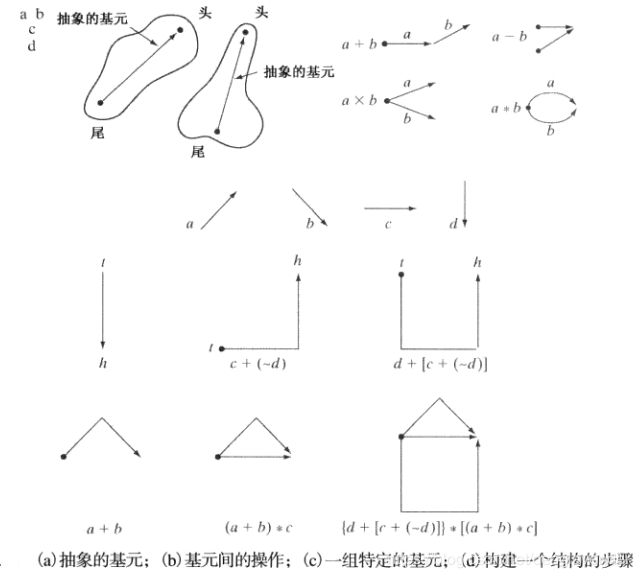
树结构关系

针对有着类似纹理或其他描绘子区域可能不连续的情况。
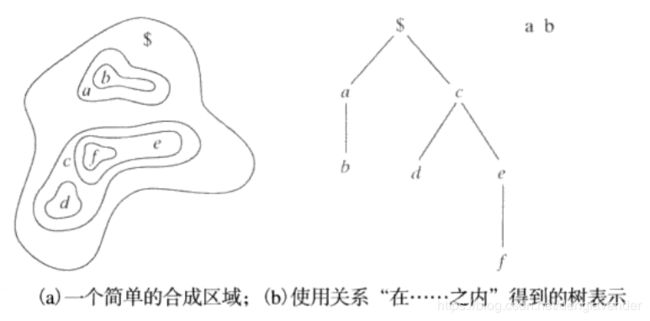
一棵树T是有着一个或多个节点的有限集合：
(a) 仅有一个表示根的节点$
(b) 余下的节点被分成不相交的集合T₁，…，T_m，每个集合依次都是一颗树，称为T的子树。

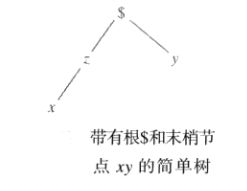
树中有两种类型的重要信息：节点信息；节点与其邻近节点相联系的信息。
用于图像描述时，两类重要的信息是：一幅图像子结构（如区域或边界）；定义该子结构和其他子结构间的物理关系。