瓜子网二手车笔试题

一、机器学习模型分类：

监督学习、非监督学习、半监督学习

1、监督学习

（1）监督学习：

从有标签的训练数据中学习模型，然后给定某个新数据，利用模型预测它的标签。

（2）泛化能力：

将模型训练出来后，适应于新样本的能力称为**“泛化能力”**

（3）监督分类的类别：

根据目标预测变量的类型不同，监督学习大体可分为回归分析和分类分析。

回归分析主要包括线性回归（linear regression）和逻辑回归（logistic regression），在某种程度上等价于函数的拟合，即选择一条函数曲线，使其能很好的拟合已知数据，并较好的预测未知数据。

回归学习常用的“损失函数”是平方损失函数，在这种情况下，回归问题通常用最小二乘法（least Squares method，LSM）来求解。

逻辑回归中，若选0.5作为阈值区分正负样本，其决策平面是：
wx+b=0

（4）最小二乘法：

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

在我们研究两个变量（x,y）之间的相互关系时，通常可以得到一系列成对的数据（x1,y1.x2,y2… xm,ym）；将这些数据描绘在x -y直角坐标系中，若发现这些点在一条直线附近，可以令这条直线方程如（式1-1）。
Yj= a0 + a1 X （式1-1) ,其中：a0、a1 是任意实数
为建立这直线方程就要确定a0和a1，应用《最小二乘法原理》，将实测值Yi与利用（式1-1）计算值（Yj=a0+a1X）的离差（Yi-Yj）的平方和〔∑（Yi - Yj）2〕最小为“优化判据”。

（5）监督学习算法：

k-近邻（k-nearest neighbor，knn）、支持向量机（support vector machine，svm）、朴素贝叶斯分类器（naive bayes）、决策树（Decision tree）、BP反向传播算法等。

（6）k-近邻（KNN）算法

算法思想：给定某个待分类的测试样本，基于某种距离（如欧几里得距离）度量，找到训练集合中与其最近的k个训练样本。然后基于这k个最近的“邻居”（k为正整数，通常很小），进行预测分类。

预测策略：
通常采用的是多数表决的“投票法”。也就是说，将这k个样本中出现最多的类别，标记为预测结果。

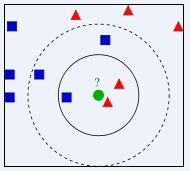
我们常说，物以类聚，人以群分，判别一个人是一个什么样品质特征的人，常常可以从他/她身边的朋友入手，所谓观其友，而识其人。我们不是要判别上图中那个绿色的圆是属于哪一类数据么，好说，从它的邻居下手。但一次性看多少个邻居呢?从上图中，你还能看到:

• 如果K=3，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。
• 如果K=5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。

k-近邻算法的不足：
首先，“多数表决”分类会砸类别分布偏斜时浮现缺陷，k的选取十分关键。
其次，“少数服从多数”原则也容易产生“多数人的暴政”问题。以多数人名义行使无限权力的情况，称为“多数人的暴政”。

解决方案：
权重：越靠近数据点的投票权重越高
距离计算：
常用的距离计算方式有欧式距离（Euclidean distance）、马氏距离（mahalanobis distance）及海明距离（hamming distance）。

（7）距离计算方式

欧式距离：

曼哈顿距离(Manhattan Distance)：

切比雪夫距离 ( Chebyshev Distance )：

闵可夫斯基距离(Minkowski Distance)：

马氏距离：

（8）懒惰学习（lazy learning）和急切学习（eager learning）：

懒惰学习：
是指他没有显式的训练过程。此类学习方法，在训练阶段仅仅将样本保存起来，所以训练时间开销为0。待收到测试样本时，才开始处理。
k-近邻算法是典型的懒惰学习。

急切学习：
是指在训练阶段就“火急火燎”的从训练样本中建模型、调参数的学习方法。

2、非监督学习

韩家炜教授曾说：“非监督学习，本质上就是聚类（cluster）的近义词”

（1）非监督学习算法：

k均值聚类（k-means clustering）、关联规则分析（association rule，如apriori算法）、主成分分析（principal components analysis，PCA）、随机森林（random forests）、受限玻尔兹曼机（restricted boltzmann Machine， RBM）等。

在深度学习里最有前景的无监督学习算法：生成对抗网络（generative adversarial networks，GAN）。

（2）k均值聚类

由聚类所生成的簇（cluster）是一组数据对象的集合，这些对象的特性是，同一个簇中的对象彼此相似，而与其他簇中的对象相异，且没有预先定义的类。

k均值聚类步骤：

K-means是一个反复迭代的过程，算法分为四个步骤：

1） 选取数据空间中的K个对象作为初始中心，每个对象代表一个聚类中心；

2） 对于样本中的数据对象，根据它们与这些聚类中心的欧氏距离，按距离最近的准则将它们分到距离它们最近的聚类中心（最相似）所对应的类；

3） 更新聚类中心：将每个类别中所有对象所对应的均值作为该类别的聚类中心，计算目标函数的值；

4） 判断聚类中心和目标函数的值是否发生改变，若不变，则输出结果，若改变，则返回2）。

k均值聚类的缺点：

• k值需要用户事先给出
• 聚类质量对初始聚类中心的选取有很强的依赖性
• 对噪声点比较敏感，聚类结果容易受噪声点的影响
• 只能发现球形簇，对于其他任意形状的簇，顿感无力

3、半监督学习

半监督学习就是以“已知之认知（标签化的分类信息）”，扩大“未知之领域（通过聚类思想将未知事物归类为已知事物）”

（1）半监督学习算法：

生成式方法、半监督支持向量机、图半监督学习、半监督聚类等

4、强化学习

“强化学习”亦称“增强学习”，但他与监督学习和非监督学习都有所不同。
强化学习强调的是：在一系列的情景下，选择最佳决策，它讲究通过多步恰当的决策，来逼近一个最优的目标，因此，它是一种序列多步决策的问题。

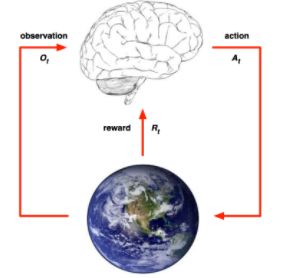
从图上我们可以看到强化学习它由两部分组成：智能体和环境。我们可以这样理解：

俗话解释一下：比如，我们从沙发旁走到门口，当我们起身之后，首先大脑获取路的位置信息，然后我们确定从当前位置向前走一步，不幸运的是我们撞墙了，这明显是个负反馈，因此环境会给我们一个负奖励，告诉我们这是一个比较差的走路方式，因此我们尝试换个方向走（走哪个方向比较好呢，后文会会讲到随机策略、确定性策略等策略决策《强化学习系列（3）：强化学习策略讲解》），就这样不断的和环境交互尝试，最终找到一套策略，确保我们能够从沙发旁边走到门口。在这个过程中会得到一个最大的累计期望奖励。

二、bootstrap数据是什么意思？（）

统计学中的方法：有放回的从样本中抽取样本

三、有效解决过拟合的方法是：

抑制过拟合的策略：

• 数据增强
• Early stopping
• 增加噪声
• 简化网络结构
• Dropout
• 贝叶斯方法

过拟合：https://www.zhihu.com/question/59201590

四、神经网络的激活函数

在深度学习中，常用的激活函数主要有：sigmoid函数，tanh函数，ReLU函数。

1、sigmoid函数

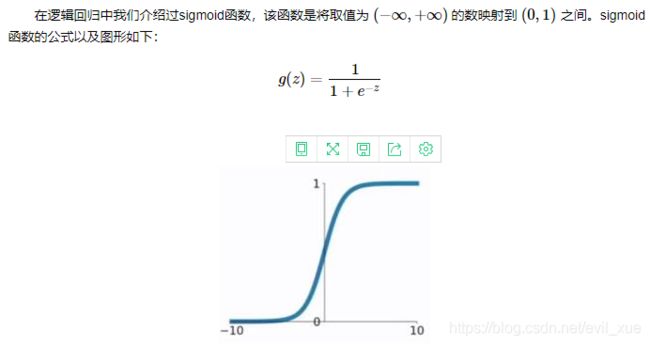
Sigmoid函数的特点是会把输出限定在0~1之间，如果是非常大的负数，输出就是0，如果是非常大的正数，输出就是1，这样使得数据在传递过程中不容易发散。

Sigmod有两个主要缺点，一是Sigmoid容易过饱和，丢失梯度。从Sigmoid的示意图上可以看到，神经元的活跃度在0和1处饱和，梯度接近于0，这样在反向传播时，很容易出现梯度消失的情况，导致训练无法完整；二是Sigmoid的输出均值不是0，基于这两个缺点，SIgmoid使用越来越少了。

2、tanh函数

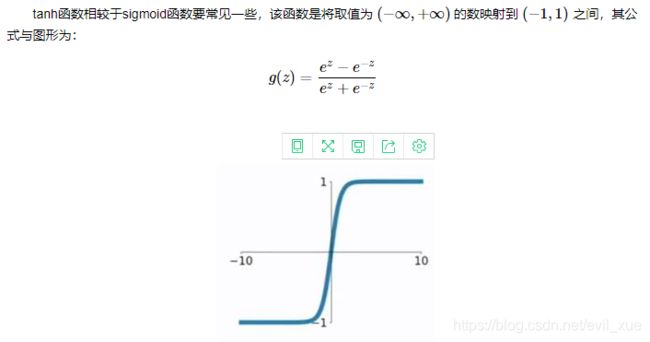
tanh是Sigmoid函数的变形，tanh的均值是0，在实际应用中有比Sigmoid更好的效果。
tanh函数的缺点同sigmoid函数的第一个缺点一样，当 zz 很大或很小时，g′(z)g′(z) 接近于 00 ，会导致梯度很小，权重更新非常缓慢，即梯度消失问题。

3、ReLU函数

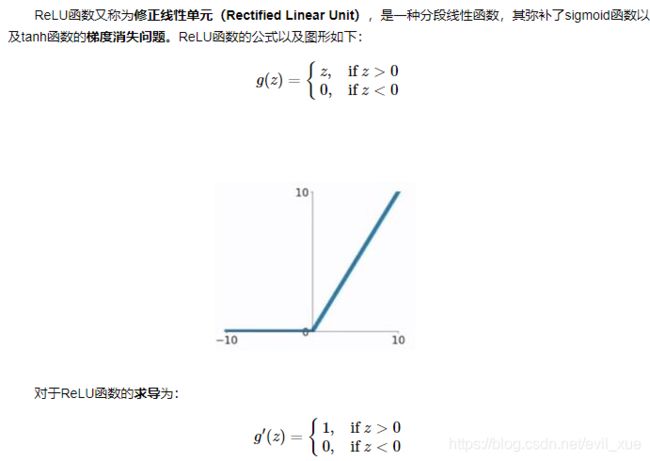
ReLU函数的优点：
  （1）在输入为正数的时候（对于大多数输入 zz 空间来说），不存在梯度消失问题。
  （2） 计算速度要快很多。ReLU函数只有线性关系，不管是前向传播还是反向传播，都比sigmod和tanh要快很多。（sigmod和tanh要计算指数，计算速度会比较慢）
   
ReLU函数的缺点：
  （1）当输入为负时，梯度为0，会产生梯度消失问题。

五、脑筋急转弯

六、哈希表 （未解答）

设哈希表长m＝14，哈希函数H（key）＝key％11。表中已有4个结点：addr(15)=4，addr(38)=5，addr(61)=6，addr(84)=7，其余地址为空。如果用二次探测再散列处理冲突，关键字为49的结点的地址是 9。

七、二进制数据的运算

1、二进制的原码、反码、补码

对于有符号数而言：
二进制的最高位是符号位：0表示正数(+)，1表示负数(-)
正数的原码、反码、补码都一样
负数的反码 = 它的符号位不变，其他位取反
负数的补码 = 它的反码 +1
0的反码、补码都是0

例题：X=+0111001,Y=+1001101,求[X-Y]补=11101100

解答：x原码=0011 1001
x补码=x原码=0011 1001

y原码=0100 1101
-y原码=1100 1101
-y反码=1011 0010
-y补码=1011 0011

[x-y]补码=x补码-y补码=x补码+[-y]补码=0011 1001 +1011 0011

2、十进制转换为二进制

除k取余法：

例题：-125 的反码是多少 1000 0010

解答：125除2取余=0111 1101（2）
-125=1111 1101
-125反码=1000 0010

八、赫夫曼树 （未解决）

例题：以数据集{1,6,8,2,9,4}为权值构造一棵赫夫曼树，其带权路径长度为 70

1、

九、数学题（未解答）

组成数字1到1234的所有数字的各位的总和是15895

解答：

十、完全二叉树计算叶子节点

完全二叉树有一个很有趣的性质：结点从1开始编号，层序。那么分每一个结点（编号为i）的左孩子结点是2i,右孩子结点编号是2i+1.
反之，根据孩子结点的编号可以推知父结点的编号：孩子结点编号的下取整。

下面是较聪明的应用：

一棵完全二叉树有1001个结点。其中叶结点的个数是：501个。

分析：1001个结点，则最后一个结点的编号是1001，那么它的父亲结点编号是500，注意，这个并不一定是倒数第二层的最后一个结点。那么从501号结点开始往后都是叶子结点，因此，叶子结点有501个。

完全一样道理的题目：

若一棵二叉树有768个结点，则该二叉树叶子结点的个数是：384个。

分析：768个结点，那么就意味着最后一个结点的父结点编号是384，从385号结点开始到最后一个全是叶子结点，因此共有384个叶子结点。

原文链接：https://blog.csdn.net/u011240016/article/details/52797592

例题：一颗完全二叉树的节点数量为666，那么这棵树上的叶子节点数为333

解答：666为偶数，2i=666,则i=333，则叶子节点为666-333.