基于卷积自编码器和图像高斯金字塔的布料缺陷无监督学习与检测方法
基于卷积自编码器和图像金字塔的布料缺陷无监督学习与检测方法
这篇博客是在我在浙江大学计算机学院做实习时接触到的一个课题,参考了论文《An Unsupervised-Learning-Based Approach for Automated Defect Inspection on Textured Surfaces》的基础上进行了复现,并加入了自己的理解和改进。
一、布料纹理缺陷检测与纹理学习
因为对缺陷进行标记或像素级分割很困难,缺陷的类型也十分复杂,所以基于学习的纹理缺陷检测大体思路是无监督的。即利用无监督学习算法学习正常纹理的数据分布特征,而不学习缺陷的数据分布特征。在待测图上以滑动区域为重构对象,与原图像做残差。由于正常纹理学习充分,重构残差应当很小,而缺陷区域的残差较大,故被凸现出来,随后再利用残差图做进一步处理。
在空域上进行无监督学习主要用卷积自编码器,其有两部分组成,编码器和解码器。编码器由卷积、激活、池化操作做成,对原始数据域分层做特征提取和降维,最后将数据映射到一个欠完备的隐层特征空间上。解码器由上采样、卷积、激活操作完成,将特征空间上的数据映射回空域。自编码器的训练一般由重构残差做为损失函数驱动,其中也可以加入稀疏正则化,提高模型泛化能力。
L ( x , x ′ ) = 1 2 N ∑ i = 1 N ∣ ∣ x − x ′ ∣ ∣ 2 + λ ⋅ ∑ w ∈ W , W ′ ∣ ∣ w ∣ ∣ F L(\bm{x},\bm{x}')=\frac{1}{2N}\sum_{i=1}^{N} || \bm{x}-\bm{x}' ||^2+\lambda \cdot \sum_{w \in W,W'}|| w ||_F L(x,x′)=2N1i=1∑N∣∣x−x′∣∣2+λ⋅w∈W,W′∑∣∣w∣∣F
式中, W W W和 W ′ W' W′是编码器和解码器的卷积核参数, ∣ ∣ ⋅ ∣ ∣ F ||\cdot||_F ∣∣⋅∣∣F表示矩阵的Frobenius范数,类似于向量的L2范数。
二、算法总述
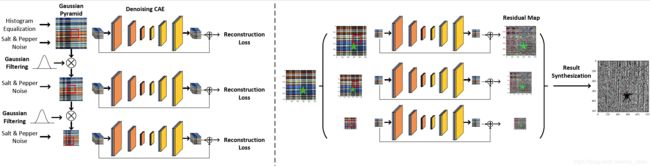
下图是算法总体框图。左侧是训练阶段,右侧是测试阶段。
训练阶段包括:图像预处理和patch提取,以及最后的分层训练。
测试阶段包括:图像预处理(但不包括噪声腐蚀)和patch提取,分层构建残差图和层间结果融合。
三、数据集准备
布料数据集是我用手机拍摄的布料视频抽取图像帧构成的。拍摄过程涉及到镜头远近(不同尺度纹理)、镜头旋转和光照不均(开闪光灯)。每张图片被裁剪成 512 × 512 512\times 512 512×512像素的彩图。缺陷主要是块状污渍和模拟缺陷。



四、训练阶段
4.1 图像预处理
- 光照归一化
- 构建高斯金字塔
- 噪声腐蚀
1)光照归一化是为了消除图像因为光照不均而引起的畸变。原文中用的是韦伯局部算子,但我没有复现出合理的归一化效果。故采用经典的直方图均衡算法。
W L D ( I ) = a r c t a n ( ∑ Δ x ∈ A ∑ Δ y ∈ A I ( x , y ) − I ( x − Δ x , y − Δ y ) I ( x , y ) ) WLD(\bm{I}) = arctan(\sum_{\Delta x \in A} \sum_{\Delta y \in A} \dfrac{ \bm{I}(x,y) - \bm{I}(x-\Delta x,y-\Delta y)}{\bm{I}(x,y)}) WLD(I)=arctan(Δx∈A∑Δy∈A∑I(x,y)I(x,y)−I(x−Δx,y−Δy))
def Illumination_Normalization(img,method = 'hist'):
'''
the function to carry out the illumination normalization using Weber Local Descriptor or Histogram Equalization
'''
height,width,channel = np.shape(img)
if method == 'hist':
# 分通道做直方图均衡
equ0 = cv2.equalizeHist(img[:,:,0])
equ1 = cv2.equalizeHist(img[:,:,1])
equ2 = cv2.equalizeHist(img[:,:,2])
img_hist_equ = np.zeros((height,width,channel),np.uint8)
img_hist_equ[:,:,0] = equ0
img_hist_equ[:,:,1] = equ1
img_hist_equ[:,:,2] = equ2
return img_hist_equ
if method == 'wld':
# 外部补零
img_padding = np.zeros((height+2,width+2,channel),np.float32)
img_padding[1:height+1,1:width+1,:] = img.astype('float32')
temp = np.zeros((height+2,width+2,channel),np.float32)
for k in range(0,channel):
for i in range(1,height+1):
for j in range(1,width+1):
temp[i,j,k] = math.atan(9- 1/img_padding[i,j,k]*(img_padding[i-1,j-1,k] + img_padding[i,j-1,k] + img_padding[i+1,j-1,k]
+img_padding[i-1,j,k] + img_padding[i,j,k] + img_padding[i+1,j,k]
+img_padding[i-1,j+1,k] + img_padding[i,j+1,k] + img_padding[i+1,j+1,k]))
temp[i,j,k] = temp[i,j,k]*180/math.pi
return temp[1:height+1,1:width+1,:]
2)金字塔的构建。图像金字塔结构一直是计算机视觉领域解决多尺度任务的利器。这里用OpenCV来实现。在实验中我采用三级结构
512 × 512 256 × 256 128 × 126 512\times 512 \\ 256\times 256 \\ 128\times 126 \\ 512×512256×256128×126
原文中没有说明作者采用何种尺寸,但根据结果图推测,其三层图像的尺寸应该非常接近,而不是我采用的跨度很大的降采样方式,感兴趣的读者可以尝试一下层间尺寸相近的金字塔构建方式,看看效果如何。
# cv2.pyrDown()只能将图像长和宽缩小为一半
# img_512是金字塔最底层的原图像
img_256 = cv2.pyrDown(img_512)
img_128 = cv2.pyrDown(img_256)
关于cv2.pyrDown()的更多说明请看 https://blog.csdn.net/woainishifu/article/details/62888228。做任意尺寸的金字塔要用到skimage先对图像做高斯卷积,再用cv2.resize()降采样。
from skimage import filters
img_out = filters.gaussian(img_in,sigma=2)
img_resize = cv2.resize(img_out,(128,128)) # (128,128)是降采样之后的尺寸
3)噪声腐蚀。噪声类型是常用的椒盐噪声。注意,这里要留有备份,一份是噪声腐蚀后的图像数据集 x ~ \tilde{\bm{x}} x~,一份是纯净的样本集 x \bm{x} x,因为论文中采用卷积去噪自编码网络,网络输入是 x ~ \tilde{\bm{x}} x~,输出是其重构 x ~ ′ \tilde{\bm{x}}' x~′,而GT是无噪声的 x \bm{x} x,所以损失函数表示为 1 2 N ∑ n = 1 N ∣ ∣ x − x ~ ′ ∣ ∣ 2 \frac{1}{2N} \sum_{n=1}^{N} ||\bm{x}-\tilde{\bm{x}}'||_2 2N1∑n=1N∣∣x−x~′∣∣2。
我给出两个椒盐噪声函数,实验中我用的是第二个,噪声系数0.01。
# 两种椒盐噪声函数
def saltpepper(img,n):
m=int((img.shape[0]*img.shape[1])*n)
for a in range(m):
i=int(np.random.random()*img.shape[1])
j=int(np.random.random()*img.shape[0])
if img.ndim==2:
img[j,i]=255
elif img.ndim==3:
img[j,i,0]=255
img[j,i,1]=255
img[j,i,2]=255
for b in range(m):
i=int(np.random.random()*img.shape[1])
j=int(np.random.random()*img.shape[0])
if img.ndim==2:
img[j,i]=0
elif img.ndim==3:
img[j,i,0]=0
img[j,i,1]=0
img[j,i,2]=0
return img
def salt_and_pepper(img,p):
temp = img
channel = img.ndim
# 灰度图
if channel == 2:
height,width = np.shape(img)[0:2]
for i in range(0,height):
for j in range(0,width):
if np.random.random() 0.5:
temp[i,j] = 0 # pepper
# 彩图
if channel == 3:
height,width = np.shape(img)[0:2]
for i in range(0,height):
for j in range(0,width):
if np.random.random() 0.5:
temp[i,j,0] = 0 # pepper
temp[i,j,1] = 0
temp[i,j,2] = 0
return temp
4.2 Patch提取
在这里讲一下论文的主要思想:论文将缺陷检测的任务看做是像素级(pixel-wised)的二分类任务,即将每个像素点分为正常纹理类和缺陷纹理类。如果仅利用该点的像素值进行分类的话,信息量不足,可以想象分类精度也不会很高。于是论文中对每个像素的 8 × 8 8\times 8 8×8邻域进行操作,利用一个小patch的区域信息作为分类依据。
插播一句:我一开始的思路和论文不一样。我选择从512像素原图中裁剪出 64 × 64 64\times 64 64×64像素的patch送入网络进行训练,然后将待测图片 x \bm{x} x不重合地裁成64像素小块 { x k ∣ k = 1 , 2 , ⋯ , N p } \{\bm{x_k}|k=1,2,\cdots,N_p\} {xk∣k=1,2,⋯,Np}进行重构,然后拼合成重构图 x ′ \bm{x}' x′,做残差图 ∣ ∣ x − x ′ ∣ ∣ 2 ||\bm{x}-\bm{x}'||_2 ∣∣x−x′∣∣2
但是结果并不理想,对于纯色块模拟的缺陷,残差图中并没有体现出来,反而是正常布料的横向竖向的纹理被减了出来,结果类似下图

我想了一个比较合理的解释是,这个自编码网络学到了一个恒等映射,而并不是把图像数据映射到隐层空间,提取其主要特征信息。所以当输入图像有缺陷时,网络也仅仅是将其恒等映射输出,仅在边缘上能体现一些残差的信息。Ian Goodfellow和G.Hinton合著的《深度学习》在自编码器章节也表达了类似的想法。
话说回来,要想有效地进行像素级分割,就要在该点附近提取patch,进行重构,得到残差patch图。由于网络训练用的全是正常布料样本,因此根据整个数据集(假设有 N p N_p Np张patch)上的残差图集就可以统计出像素点的重构残差(每个patch代表原图中一个pixel)的均值和方差。注意到每个点都是代表正常纹理的,因此这个残差分布反映了正常纹理的数据分布特征。
多说一句,实验表明该分布是一个重拖尾的高斯分布,取分类阈值 T ( i ) = μ ( i ) + γ ⋅ σ ( i ) T^{(i)}=\mu^{(i)}+\gamma \cdot \sigma^{(i)} T(i)=μ(i)+γ⋅σ(i),若待测图中某点残差高于 T ( i ) T^{(i)} T(i),则分类为缺陷像素点。
训练过程的patch提取是有重合的。滑动步长为4,patch尺寸 8 × 8 8 \times 8 8×8,可以计算出金字塔三层(512图31张,256图31张,128图31张)的patch各有499999、123039、29791。
# 裁切图片
# 原图像512像素的路径
img_dir_layer1 = './pyramid/layer1/'
filelist = os.listdir(img_dir_layer1)
# 裁剪之后的图像矩阵
img_512_crop = np.zeros((127*127*len(filelist),8,8,3),np.uint8)
count = 0
for i in range(len(filelist)):
img_512 = cv2.imread(img_dir_layer1+filelist[i])
for j in range(0,127):
for k in range(0,127):
img_512_crop[count,:,:,:] = img_512[4*j:4*j+8,4*k:4*k+8,:]
count += 1
print('done!')
# 原图像256像素
img_dir_layer2 = './pyramid/layer2/'
filelist = os.listdir(img_dir_layer2)
# 裁剪之后的图像矩阵
img_256_crop = np.zeros((63*63*len(filelist),8,8,3),np.uint8)
count = 0
for i in range(len(filelist)):
img_256 = cv2.imread(img_dir_layer2+filelist[i])
for j in range(0,63):
for k in range(0,63):
img_256_crop[count,:,:,:] = img_256[4*j:4*j+8,4*k:4*k+8,:]
count += 1
print('done!')
# 原图像128像素
img_dir_layer3 = './pyramid/layer3/'
filelist = os.listdir(img_dir_layer3)
# 裁剪之后的图像矩阵
img_128_crop = np.zeros((31*31*len(filelist),8,8,3),np.uint8)
count = 0
for i in range(len(filelist)):
img_128 = cv2.imread(img_dir_layer3+filelist[i])
for j in range(0,31):
for k in range(0,31):
img_128_crop[count,:,:,:] = img_128[4*j:4*j+8,4*k:4*k+8,:]
count += 1
print('done!')
# 多次打乱顺序,使之完全shuffled
for i in range(0,10):
np.random.shuffle(img_512_crop)
np.random.shuffle(img_256_crop)
np.random.shuffle(img_128_crop)
# 将裁剪后的图片矩阵保存
img_512_crop_out = open('512_crop.pkl','wb')
pickle.dump(img_512_crop,img_512_crop_out)
img_512_crop_out.close()
img_256_crop_out = open('256_crop.pkl','wb')
pickle.dump(img_256_crop,img_256_crop_out)
img_256_crop_out.close()
img_128_crop_out = open('128_crop.pkl','wb')
pickle.dump(img_128_crop,img_128_crop_out)
img_128_crop_out.close()
4.3网络结构与训练
论文中并没有提到具体的网络结构,我经尝试,构造的结构如下图所示。
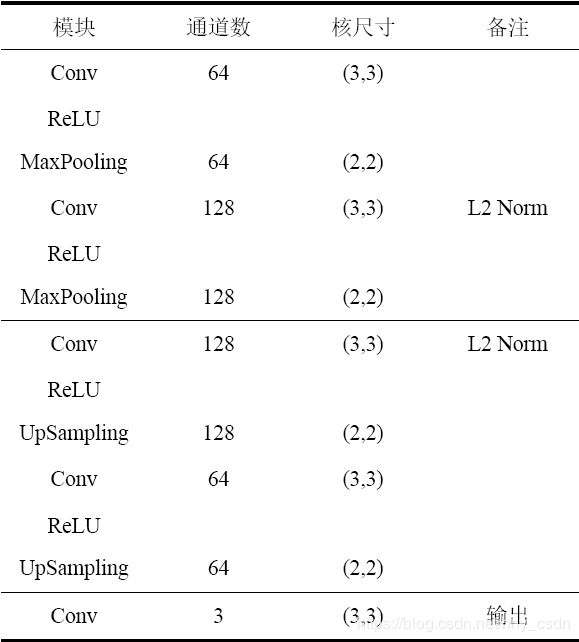
其中损失函数的L2正则项权重 λ = 0.001 \lambda=0.001 λ=0.001, s t r i d e = 1 × 1 stride=1\times 1 stride=1×1
写程序的时候还有一点要注意,png图片用OpenCV读进来是uint8格式的np.array,建议将其转化成np.float32,并除以255归一化,否则卷积网络无法训练。另外,以float32格式的像素值区间为[0,255]的话,plt.imshow()显示图片是会失真的。
# 参数设置
batch_size = 64
epochs = 50
img_rows, img_cols = 8, 8 # 输入图片尺寸
input_shape = (img_rows, img_cols, 3)
model_name = './pyramid/model/convergence_evaluation.h5'
# 数据类型转换前应该是uint8
X_train = img_512_train
X_train = X_train.astype('float32')
X_train /= 255
print('X_train shape:', X_train.shape)
print(X_train.shape[0], 'train samples')
#构建模型
model = Sequential()
"""
model.add(Convolution2D(nb_filters, kernel_size[0], kernel_size[1],
border_mode='same',
input_shape=input_shape))
"""
model.add(Convolution2D(64, (3, 3), padding='same', input_shape=input_shape)) # 卷积层1
model.add(Activation('relu')) #激活层
model.add(MaxPooling2D((2,2))) #池化层1
model.add(Convolution2D(128, (3, 3),padding='same',kernel_regularizer=regularizers.l2(0.001))) #卷积层2
model.add(Activation('relu')) #激活层
model.add(MaxPooling2D((2,2))) #池化层2
#model.add(Convolution2D(256, (3, 3),padding='same',kernel_regularizer=regularizers.l2(0.001))) #卷积层3
#model.add(Activation('relu')) #激活层
#model.add(MaxPooling2D((2,2))) #池化层3
#model.add(Convolution2D(256, (3, 3),padding='same',kernel_regularizer=regularizers.l2(0.001))) #卷积层4
#model.add(Activation('relu')) #激活层
#model.add(UpSampling2D((2,2))) #上采样层1
model.add(Convolution2D(128, (3, 3),padding='same',kernel_regularizer=regularizers.l2(0.001))) #卷积层5
model.add(Activation('relu')) #激活层
model.add(UpSampling2D((2,2))) #上采样层2
model.add(Convolution2D(64, (3, 3),padding='same')) #卷积层6
model.add(Activation('relu')) #激活层
model.add(UpSampling2D((2,2))) #上采样层3
model.add(Convolution2D(3, (3, 3),padding='same')) #卷积层7
model.add(Activation('sigmoid')) #激活层
model.summary()
#编译模型
adam = optimizers.Adam()
model.compile(loss='mse', # model.compile(loss='categorical_crossentropy', #
optimizer=adam,
metrics=['accuracy']) # mse
#训练模型 verbose=1表示显示训练进度条
model.fit(X_train, X_train,
epochs=epochs,
batch_size=batch_size,
shuffle=True,verbose=1)
model.save(model_name)
4.4阈值确定
设第 i i i层金字塔的训练集有 N p N_p Np个patch,也就有 N p N_p Np个残差 ϑ ( i ) ( x ) \vartheta^{(i)}(\bm{x}) ϑ(i)(x)。则残差集合表示为
ξ ( i ) = { ϑ ( i ) ( x k ) ∣ k = 1 , 2 , ⋯ , N p } \xi^{(i)}=\{ \vartheta^{(i)}(\bm{x}_k)| k=1,2,\cdots,N_p\} ξ(i)={ϑ(i)(xk)∣k=1,2,⋯,Np}
残差计算如下公式,注意,这是对一个patch计算得到一个值。
ϑ ( i ) ( x ) = ∣ ∣ x − x ~ ′ ∣ ∣ 2 = ∑ i = 1 8 ∑ j = 1 8 ∑ k = 1 3 ( x i j k − x ~ i j k ′ ) 2 \vartheta^{(i)}(\bm{x}) = || \bm{x}-\tilde{\bm{x}}' ||_2=\sum_{i=1}^{8}\sum_{j=1}^{8}\sum_{k=1}^{3}(\bm{x}_{ijk}-\tilde{\bm{x}}_{ijk}')^2 ϑ(i)(x)=∣∣x−x~′∣∣2=i=1∑8j=1∑8k=1∑3(xijk−x~ijk′)2
在 ξ ( i ) \xi^{(i)} ξ(i)集合上对 N p N_p Np个残差值统计,得到其直方图统计和均值 μ ( i ) \mu^{(i)} μ(i)、方差 σ ( i ) \sigma^{(i)} σ(i)等信息。
当然,你也可以分通道计算阈值,也就是RGB三个通道各确定一个阈值,随后的分割操作也是分通道进行,不过我的实验没发现什么有益的变化。

红线是金字塔第一层的499999个重构patch的残差值的频数直方图,蓝线是我模拟的块状纯色缺陷的残差分布,竖线是 T ( 1 ) = μ ( 1 ) + 2 σ ( 1 ) T^{(1)}=\mu^{(1)}+2\sigma^{(1)} T(1)=μ(1)+2σ(1)。根据高斯分布的 3 σ 3\sigma 3σ准则,在 [ μ − 2 σ , μ + 2 σ ] [\mu-2\sigma,\mu+2\sigma] [μ−2σ,μ+2σ]的区间内,包含了95.5%以上的样本,因此我们在这里设置阈值,将其与缺陷分割。
这一步实际上是在构建一个简单的分类器,即
ξ ( i ) ( x j , k ) = { 0 , i f ϑ ( i ) ( x j , k ) ≤ T ( i ) 1 , o t h e r \xi^{(i)}(\bm{x}_{j,k}) =\left\{ \begin{array}{rcl} 0, & & if \ \vartheta^{(i)}(\bm{x}_{j,k}) \le T^{(i)} \\ 1, & & other \end{array}\right. ξ(i)(xj,k)={0,1,if ϑ(i)(xj,k)≤T(i)other
所以论文也采用了虚警率、准确率、查全率等等指标来衡量分割效果的好坏。注意的是,论文说作者准备了200张没有缺陷的样本(512像素),200张有缺陷的样本(512像素),但是并不清楚它的ground truth是怎么标记的。另外,根据上下文判断,虚警率、准确率、查全率都是针对某张图片中的所有像素点为样本全体来进行统计的。
# 训练图片的重构集
model_512 = load_model('./pyramid/model/CAE_512_53_35.h5')
model_256 = load_model('./pyramid/model/CAE_256_53_35.h5')
model_128 = load_model('./pyramid/model/CAE_128_53_35.h5')
img_512_train_float = img_512_train.astype('float32')
img_512_train_float /= 255
img_256_train_float = img_256_train.astype('float32')
img_256_train_float /= 255
img_128_train_float = img_128_train.astype('float32')
img_128_train_float /= 255
img_reconstruct_512 = model_512.predict(img_512_train_float,verbose=1)
img_reconstruct_256 = model_256.predict(img_256_train_float,verbose=1)
img_reconstruct_128 = model_128.predict(img_128_train_float,verbose=1)
# 训练集的残差图集
residual_512 = img_512_train_float - img_reconstruct_512
residual_256 = img_256_train_float - img_reconstruct_256
residual_128 = img_128_train_float - img_reconstruct_128
# 残差集是以每张图片为对象,将其64*64个值,先平方,再求和,再求跟,||x-x'||
res_512 = np.zeros((len(residual_512)))
res_256 = np.zeros((len(residual_256)))
res_128 = np.zeros((len(residual_128)))
for i in range(0,len(residual_512)):
# 对每一个patch求残差
temp = residual_512[i,:,:,:]**2
res_512[i] = temp.sum()
res_512[i] = np.sqrt(res_512[i])
print('512 ok')
for i in range(0,len(residual_256)):
# 对每一个patch求残差
temp = residual_256[i,:,:,:]**2
res_256[i] = temp.sum()
res_256[i] = np.sqrt(res_256[i])
print('256 ok')
for i in range(0,len(residual_128)):
# 对每一个patch求残差
temp = residual_128[i,:,:,:]**2
res_128[i] = temp.sum()
res_128[i] = np.sqrt(res_128[i])
print('128 ok')
# 求残差集的均值与标准差
res_mean_512 = res_512.mean()
res_std_512 = res_512.std()
res_mean_256 = res_256.mean()
res_std_256 = res_256.std()
res_mean_128 = res_128.mean()
res_std_128 = res_128.std()
# 确定分割阈值
gamma = 2
T_512 = res_mean_512 + gamma * res_std_512
T_256 = res_mean_256 + gamma * res_std_256
T_128 = res_mean_128 + gamma * res_std_128
计算直方图
(n, bins) = numpy.histogram(res_512[:,0], bins=200) # NumPy version (no plot)
plt.plot(.5*(bins[1:]+bins[:-1]), n,'r')
(n, bins) = numpy.histogram(res_pure, bins=200) # NumPy version (no plot)
plt.plot(.5*(bins[1:]+bins[:-1]), n,'b')
plt.axvline(T_512_0) # 画竖线
plt.xlabel('residual of reconstruction',fontproperties=zh_font)
plt.ylabel('number of pixels',fontproperties=zh_font)
#.show()
plt.savefig('residual_histogram.png')
五、模型测试阶段
模型的测试也分为图像预处理、patch提取、残差图构建、分割缺陷和结果综合几步。
5.1 图像预处理
图像预处理包括光照归一化、高斯金字塔构建。但不包括噪声腐蚀。
代码在最下面。
5.2 patch提取
这里要牺牲一点原图像外圈的像素,因为要在待分割的像素点周围提取8x8的patch,所以外围4个pixel宽度的边缘是没法做的。该步的滑动步长为1。
5.3 残差图构建
将每个patch送入网络进行重构,得到重构图,按上述公式计算方法算出一个值。

5.4 缺陷分割
将算出来的残差值与阈值比对,得到分割结果。此时我们可以在金字塔每层得到一张尺寸各异的二值图,标记了每个像素的分割结果。
5.5 结果综合
这一步将金字塔各层的分割结果进行综合,以降低错分提高精度。
我的做法是:
1)将所有层结果的尺寸归一化到最高层,即最小尺寸。此时图像不再是二值图,所以进行四舍五入恢复。
2)对相邻两层的对应像素点,进行逻辑与操作。
ξ i , i + 1 ( x ) = ξ ( i ) ( x ) ξ ( i + 1 ) ( x ) \xi^{i,i+1}(\bm{x}) = \xi^{(i)}(\bm{x}) \xi^{(i+1)}(\bm{x}) ξi,i+1(x)=ξ(i)(x)ξ(i+1)(x)
3)对所有层的对应像素点,做逻辑或操作。
ς ( x ) = ξ 1 , 2 ( x ) ∣ ξ 2 , 3 ( x ) ∣ ⋯ ∣ ξ n − 1 , n ( x ) \varsigma(\bm{x}) = \xi^{1,2}(\bm{x}) \ | \ \xi^{2,3}(\bm{x}) \ | \cdots | \ \xi^{n-1,n}(\bm{x}) ς(x)=ξ1,2(x) ∣ ξ2,3(x) ∣⋯∣ ξn−1,n(x)
最后结果如下

# 三通道合一进行分割
# 读入缺陷图
img_dir_defect = './pyramid/defective/'
filelist = os.listdir(img_dir_defect)
img_defect_512 = np.zeros((len(filelist),512,512,3),np.uint8)
img_defect_256 = np.zeros((len(filelist),256,256,3),np.uint8)
img_defect_128 = np.zeros((len(filelist),128,128,3),np.uint8)
for i in range(len(filelist)):
img_defect_512[i] = cv2.imread(img_dir_defect+filelist[i])
# 光照归一化
img_defect_512[i] = Illumination_Normalization(img_defect_512[i])
# 三级金字塔
img_defect_256[i] = cv2.pyrDown(img_defect_512[i])
img_defect_128[i] = cv2.pyrDown(img_defect_256[i])
# 转换成浮点型,并归一化
img_defect_512_float = img_defect_512.astype('float32')
img_defect_512_float /= 255
img_defect_256_float = img_defect_256.astype('float32')
img_defect_256_float /= 255
img_defect_128_float = img_defect_128.astype('float32')
img_defect_128_float /= 255
# 导入模型
model_512 = load_model('./pyramid/model/CAE_512_53_35.h5')
model_256 = load_model('./pyramid/model/CAE_256_53_35.h5')
model_128 = load_model('./pyramid/model/CAE_128_53_35.h5')
# 分割图像
img_defect_seg_512 = np.zeros((len(img_defect_512),505,505))
img_defect_seg_256 = np.zeros((len(img_defect_256),249,249))
img_defect_seg_128 = np.zeros((len(img_defect_128),121,121))
temp = np.zeros((len(img_defect_512),8,8,3))
# 不重叠地裁剪成8*8大小的patch,进行重构
for i in range(3,508):
for j in range(3,508):
# 对缺陷图进行操作
temp = model_512.predict(img_defect_512_float[:,i-3:i+5,j-3:j+5,:],verbose=0)
for k in range(len(img_defect_512)):
# temp表示一个pixel的邻域的重构图像
temp1 = (temp[k] - img_defect_512_float[k,i-3:i+5,j-3:j+5,:])**2
temp2 = temp1.sum()
temp2 = np.sqrt(temp2)
if temp2>T_512:
img_defect_seg_512[k,i-3,j-3] = 1
else:
img_defect_seg_512[k,i-3,j-3] = 0
print('done')
for i in range(3,252):
for j in range(3,252):
# 对缺陷图进行操作
temp = model_256.predict(img_defect_256_float[:,i-3:i+5,j-3:j+5,:],verbose=0)
for k in range(len(img_defect_256)):
# temp表示一个pixel的邻域的重构图像
temp1 = (temp[k] - img_defect_256_float[k,i-3:i+5,j-3:j+5,:])**2
temp2 = temp1.sum()
temp2 = np.sqrt(temp2)
if temp2>T_256:
img_defect_seg_256[k,i-3,j-3] = 1
else:
img_defect_seg_256[k,i-3,j-3] = 0
print('done')
for i in range(3,124):
for j in range(3,124):
# 对缺陷图进行操作
temp = model_128.predict(img_defect_128_float[:,i-3:i+5,j-3:j+5,:],verbose=0)
for k in range(len(img_defect_128)):
# temp表示一个pixel的邻域的重构图像
temp1 = (temp[k] - img_defect_128_float[k,i-3:i+5,j-3:j+5,:])**2
temp2 = temp1.sum()
temp2 = np.sqrt(temp2)
if temp2>T_128:
img_defect_seg_512[k,i-3,j-3] = 1
else:
img_defect_seg_512[k,i-3,j-3] = 0
print('done')
# 存储缺陷图处理结果
with open('defect_512.pkl','wb') as f:
pickle.dump(img_defect_seg_512,f)
with open('defect_256.pkl','wb') as f:
pickle.dump(img_defect_seg_256,f)
with open('defect_128.pkl','wb') as f:
pickle.dump(img_defect_seg_128,f)