ufldl.PCA-2D实现
Step 0: Load data
用文本方式打开pcaData.txt,看到的就是两行数据,每行有45个值。
不加’-ascii’,直接写出x=load(‘pcaData.txt’)也是ok 的!
figure(1)表明建立第一幅图像,在需要显示很多图像的时候就需要用到这一句了。
scatter则是画图函数,这里的x轴数据为x的第一行数据x(1,:),y轴数据为x的第二行数据x(2,:)。
最后给第一副图像命名为’Raw data’,此时显示的图像里边就只有原始数据信息。
%% Step 0: Load data
% We have provided the code to load data from pcaData.txt into x.
% x is a 2 * 45 matrix, where the kth column x(:,k) corresponds to
% the kth data point.Here we provide the code to load natural image data into x.
% You do not need to change the code below.
x = load('pcaData.txt','-ascii');
figure(1);
scatter(x(1, :), x(2, :));
title('Raw data');Step 1a: Implement PCA to obtain U
这一步要做的就是求取旋转矩阵U,设输入数据为m*n的矩阵,n为样本数,m为每个样本的特征维数。
U=[ u1 u2 … um ],其中的任一 ui 都是一个m维的列向量,所以U也是一个m*m维的矩阵。
求取U的方式是:
1.首先得到样本数据的协方差矩阵
2.求取协方差矩阵的特征值与对应特征向量
3.对特征值进行排序,根据顺序得到的特征向量依次组成U
% -------------------- YOUR CODE HERE --------------------
U = zeros(size(x, 1)); % You need to compute this
%{
sigma = zeros(size(x,1), size(x,1));
for i = 1:size(x,2)
sigma = sigma + x(:,i)*x(:,i)';
end
sigma = sigma/size(x,2);
%}
sigma = x * x' / size(x, 2);
[V, D] =eig(sigma);
sortV = [V' diag(D) abs(diag(D))];
sortV = sortrows(sortV, -(size(V, 1)+2));
U = sortV(:,1:size(V,1))';
%[U, S, V] = svd(sigma);
% --------------------------------------------------------
hold on
plot([0 U(1,1)], [0 U(2,1)]);
plot([0 U(1,2)], [0 U(2,2)]);
scatter(x(1, :), x(2, :));
hold off协方差矩阵
上面代码中sigma便是求取得到的协方差矩阵。
首先来看看我注释掉的这段代码
sigma = zeros(size(x,1), size(x,1));
for i = 1:size(x,2)
sigma = sigma + x(:,i)*x(:,i)';
end
sigma = sigma/size(x,2);x(:,i)是第i个样本,是一个m*1维的列向量,所以 x(:,i)∗x(:,i)′ 得到的就是一个m*m维的矩阵。
对于这n个样本,每个样本都会产生一个m*m维的矩阵,将这n个矩阵相加,然后再求个平均值(即对矩阵的每个元素都除以n)就得到了协方差矩阵sigma。
向量化版本也就是
sigma = x * x' / size(x, 2);我以 xi 代表x(:,i), xi 是一个m*1的列向量, x′i 是 xi 的转置,所以是个 1∗m 的行向量。
那么 x=(x1 x2 ... xn)
x′=(x′1;x′2;…;x′n)
所以 x∗x′=∑ni=1xi∗x′i ,这和上面的for循环版本是一致的!
除了使用eig还可以使用svd矩阵分解求出特征向量的哦!
[V, D] =eig(sigma);特征向量V是个m*m的矩阵,每一列代表一个特征向量,而D则是一个对角矩阵,在对角元素上存储了对应特征值,所以通过diag(D)操作可以得到一个特征值组成的列向量。
求取出协方差矩阵的特征值与特征向量之后,需要根据特征值绝对值大小进行降序排序。
所以构造sortV结构,每一行存储一个特征向量(此时转换为行向量形式),并接上特征值以及特征值的绝对值,之所以这样存储是为了排序方便,用列的话就不好用matlab来排序了。如下,V经过一个转置之后加上特征值以及特征值的abs。
sortV = [V’ diag(D) abs(diag(D))];
构造好之后就可以进行排序了。
这里使用的是sortrows函数,根据sortV的第size(V, 1)+2列的值对每一行进行排序,注意是根据列的值进行排序!!。默认是按照升序排列,所以加个-号表示降序!
sortV = sortrows(sortV, -(size(V, 1)+2));
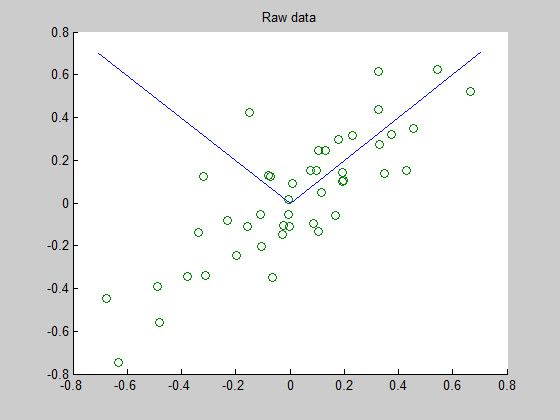
U = sortV(:,1:size(V,1))';plot则是画出两条特征向量,这两条特征向量在接下来会成为新的映射轴(可以看作是新的x,y轴)。
因为要在一幅图上画,所以要加hold on,画完之后则加上hold off。
plot([0 U(1,1)],[0 U(2,1)]表示在(0,0)与(U(1,1),U(2,1))之间画条线,这就是第一个特征向量了。
U(1,1),U(2,1)正好是U的第一列的值哦!
我得到的结果如下:
Step 1b: Compute xRot, the projection on to the eigenbasis
得到U之后就可以对原始数据x进行映射啦!
做以下操作 xnew=U∗x ,新得到的 xnew 也是一个m*n维的矩阵,此时的U只是对x进行了一个旋转变换,并没有进行降维的处理。
x=(x1 x2 ... xn)
U=(u1 u2 ... um)
xRot=U′∗x=⎡⎣⎢⎢⎢⎢u′1u′2...u′m⎤⎦⎥⎥⎥⎥∗(x1 x2 … xn)
=⎡⎣⎢⎢⎢⎢u′1∗x1u′2∗x1...u′m∗x1u′1∗x2u′2∗x2u′m∗x2.........u′1∗xnu′2∗xnu′m∗xn⎤⎦⎥⎥⎥⎥
所以xRot的第一列便是 x1 在经过映射之后的新值了!
xRot = zeros(size(x)); % You need to compute this
xRot = U'*x;
% --------------------------------------------------------
% Visualise the covariance matrix. You should see a line across the
% diagonal against a blue background.
figure(2);
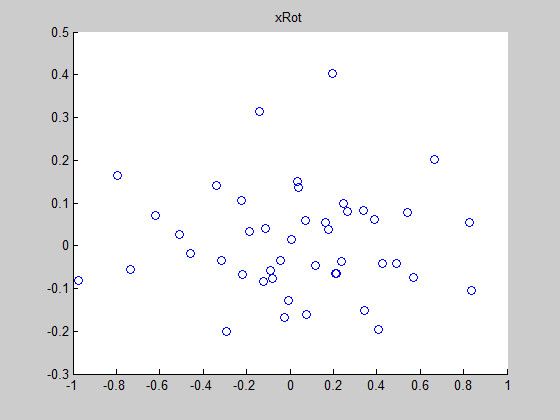
scatter(xRot(1, :), xRot(2, :));
title('xRot');
U =
0.7055 -0.7087
0.7087 0.7055
sortV =
0.7055 0.7087 0.1620 0.1620
-0.7087 0.7055 0.0154 0.0154
Step 2: Reduce the number of dimensions from 2 to 1
降维是怎么做的呢?直接取U的前k列就可以吗?
来做做推导:
我用uHat记录U的前k列,所以 uHat=(u1 u2 ... uk) ,剩下的n-k列我就不管了啊,看看能不能正常运行下。
xHat=uHat′∗x=⎡⎣⎢⎢⎢⎢u′1u′2...u′k⎤⎦⎥⎥⎥⎥∗(x1 x2 … xn)
=⎡⎣⎢⎢⎢⎢u′1∗x1u′2∗x1...u′k∗x1u′1∗x2u′2∗x2u′k∗x2.........u′1∗xnu′2∗xnu′k∗xn⎤⎦⎥⎥⎥⎥
果然可以欸,xHat的每一列也只有k维了!
看来只需要记录下前k个特征向量就可以啦!
代码如下
k = 1; % Use k = 1 and project the data onto the first eigenbasis
xHat = zeros(size(x)); % You need to compute this
uHat = zeros(size(U));
uHat(:,1:k) = U(:,1:k);
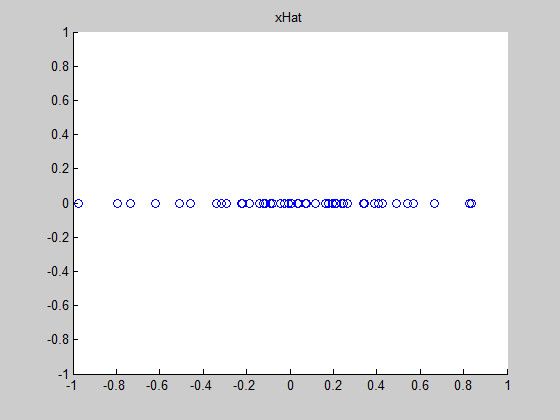
xHat = uHat'*x;Step 3: PCA Whitening
PCA白化的作用是使得经过PCA变换后所有样本在每一维上的方差为1!!
注意是对所有样本而言,而不是对单个样本的所有属性。
首先来看看变换之前xRot的方差情况。
xRot(1,:)是所有样本第一维的属性,xRot(2,:)是所有样本第二维的属性。
协方差矩阵xRot*xRot’/45的对角线上边得到的就是各个属性上的方差值。
下面计算的稍微有点误差,不过不影响观看。
xRot*xRot’/45
ans =
0.1620 -0.0000
-0.0000 0.0154
cov(xRot(1,:))
ans =
0.1644
cov(xRot(2,:))
ans =
0.0156
sortV(:,size(x,1)+2)
ans =
0.1620
0.0154
我们注意到两个方差分别对应特征值哦!!
cov(xRot(1,:))=(1/n)∗∑ni=1(xRot(1,i)−mean(xRot(1,:)))=λ1
所以我们给xRot的第一行乘以一个 1/λ1−−√ ,这样第一行的cov就变成1啦!!
白化的思想就是这样,所以对于xRot的第i行,我们乘以 1/λi−−√ 就ok了!
代码如下:
bsxfun里边的@times是乘的意思。
xPCAWhite = zeros(size(x)); % You need to compute this
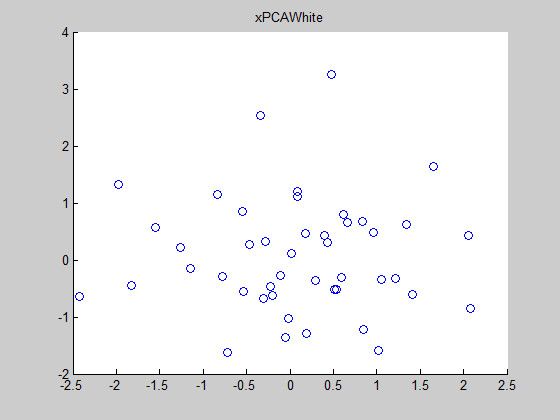
xPCAWhite = bsxfun(@times, xRot, sqrt(1./sortV(:,size(V,1)+2)));效果如下:
xPCAWhite*xPCAWhite’/45
ans =
1.0000 0.0000
0.0000 1.0000
cov(xPCAWhite(1,:))
ans =
1.0147
cov(xPCAWhite(2,:))
ans =
1.0170
记录一下bsxfun里边的各种@
@plus
Plus
@minus
Minus
@times
Array multiply
@rdivide
Right array divide
@ldivide
Left array divide
@power
Array power
@max
Binary maximum
@min
Binary minimum
@rem
Remainder after division
@mod
Modulus after division
@atan2
Four quadrant inverse tangent
@hypot
Square root of sum of squares
@eq
Equal
@ne
Not equal
@lt
Less than
@le
Less than or equal to
@gt
Greater than
@ge
Greater than or equal to
@and
Element-wise logical AND
@or
Element-wise logical OR
@xor
Logical exclusive OR
Step 3: ZCA Whitening
我们已知 xRot=UT∗x
这里 UT=U′ ,是U的转置。
因为U是正交矩阵,所以有 UUT=UTU=I
所以 x=U∗xRot=U∗UT∗x=I∗x=x
又有 xPCAWhite,i=(xRot,i)/λi−−√
最后 xZCAWhite=U∗xPCAWhite
感觉就像是数据经过了一下PCA变换,然后PCA白化了一下,接着又变换到了原来的坐标系上,因为PCA操作得到的坐标系是互不相干的,所以等于将数据做了个去相关操作,最后变换回原始坐标系上,使得数据尽可能接近原始数据,这样就是ZCA白化了。
xZCAWhite = zeros(size(x)); % You need to compute this
xZCAWhite = sortV(:,1:size(V,1))'*xPCAWhite;
% --------------------------------------------------------
figure(5);
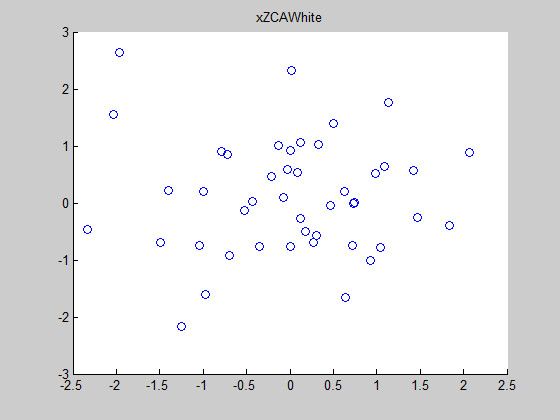
scatter(xZCAWhite(1, :), xZCAWhite(2, :));
title('xZCAWhite');正则化问题
在PCA白化的时候,需要除以一个 λi−−√ ,可是当这个特征值很小很小接近0的时候该怎么办啊?如果直接除,那么会使数据变大好多哦。
所以在实践中一般是会加个很小的常数 ϵ ,也就是变成 λi+ϵ−−−−−√ 。
(和这个问题很相似的还有朴素贝叶斯分类问题)
加上这个常数项的好处还有对图像的平滑作用,消除噪声。