DataWhale组队学习Task1-OpenCV框架与图像插值算法
图像插值算法和OpenCV实现
常用插值算法
1.最近邻插值算法
最近邻插值,是指将目标图像中的点,对应到源图像中后,找到最相邻的整数点,作为插值后的输出。
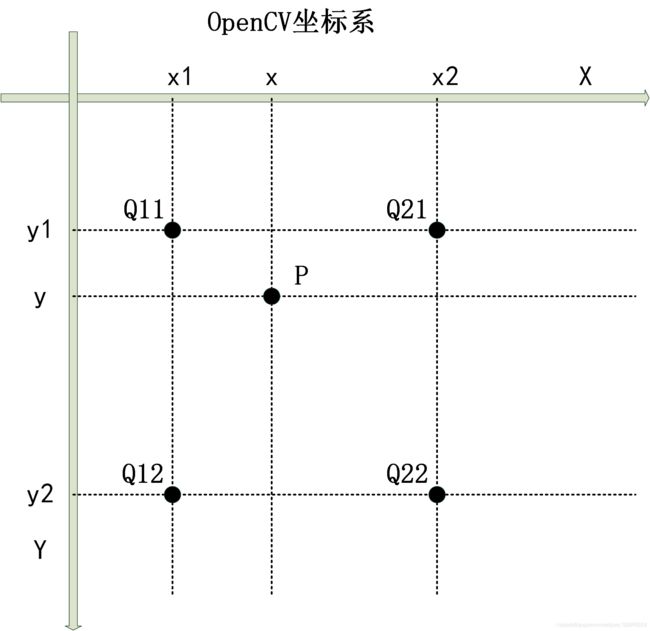
如上图所示,目标图像中的某点投影到原图像中的位置为点P,此时易知, f ( P ) = f ( Q 11 ) f(P)=f(Q_{11}) f(P)=f(Q11)
一个例子:
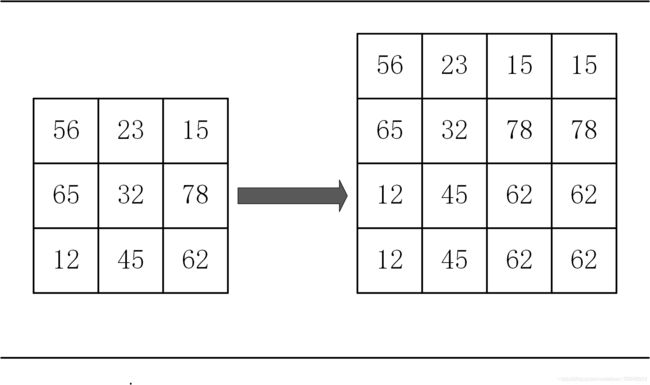
如下图所示,将一幅3X3的图像放大到4X4,用 f ( x , y ) f(x,y) f(x,y)表示目标图像, h ( x , y ) h(x,y) h(x,y)表示原图像,我们有如下公式:
f ( d s t X , d s t Y ) = h ( d s t X ∗ s r c w i d t h d s t w i d t h , d s t Y ∗ s r c h e i g h t d s t h e i g h t ) f(dst_X,dst_Y)=h(\frac {dst_X*src_{width}}{dst_{width}},\frac {dst_Y*src_{height}}{dst_{height}}) f(dstX,dstY)=h(dstwidthdstX∗srcwidth,dstheightdstY∗srcheight)
f ( 0 , 0 ) = h ( 0 , 0 ) f(0,0)=h(0,0) f(0,0)=h(0,0)
f ( 0 , 1 ) = h ( 0 , 0.75 ) = h ( 0 , 1 ) f(0,1)=h(0,0.75)=h(0,1) f(0,1)=h(0,0.75)=h(0,1)
f ( 0 , 2 ) = h ( 0 , 1.50 ) = h ( 0 , 2 ) f(0,2)=h(0,1.50)=h(0,2) f(0,2)=h(0,1.50)=h(0,2)
f ( 0 , 3 ) = h ( 0 , 2.25 ) = h ( 0 , 2 ) f(0,3)=h(0,2.25)=h(0,2) f(0,3)=h(0,2.25)=h(0,2)
…
缺点:
用该方法作放大处理时,在图象中可能出现明显的块状效应
原始图片:
大小:200x150

最临近差值放大
500x300

2.双线性差值
在讲双线性插值之前先看以一下线性插值,线性插值多项式为:
f ( x ) = a 1 x + a 0 f(x)=a_1x+a_0 f(x)=a1x+a0
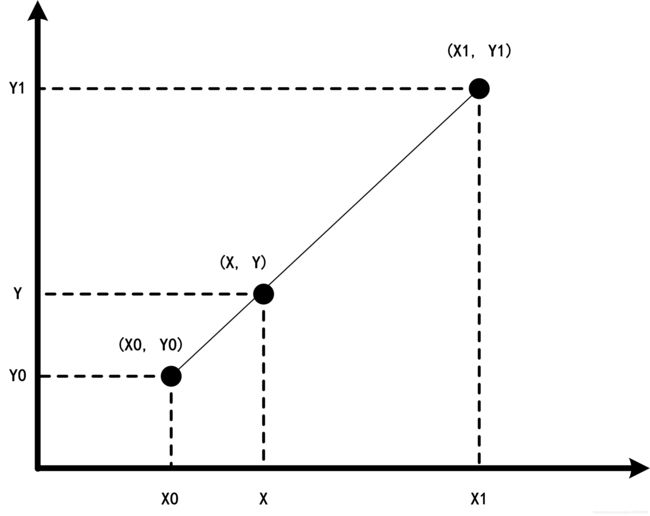
y = y 0 + ( x − x 0 ) y 1 − y 0 x 1 − x 0 y=y_0+(x-x_0)\frac {y_1-y_0}{x_1-x_0} y=y0+(x−x0)x1−x0y1−y0= y 0 + ( x − x 0 ) y 1 − ( x − x 0 ) y 0 x 1 − x 0 y_0+\frac{(x-x_0)y_1-(x-x_0)y_0}{x_1-x_0} y0+x1−x0(x−x0)y1−(x−x0)y0
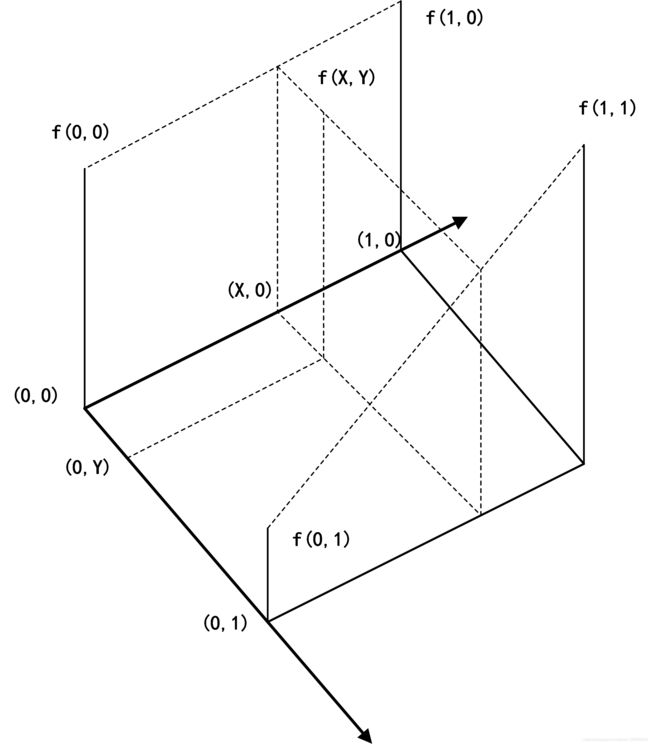
双线性插值就是线性插值在二维时的推广,在两个方向上做三次线性插值,具体操作如下图所示:
基于opencv的实现
import cv2
img=cv2.imread('./tree.jpg')
cv2.imshow('tree',img)
h,w=img.shape[:2]
img_near=cv2.resize(img,(int(w*1.5),int(h*1.5)),interpolation=cv2.INTER_NEAREST)
cv2.imshow('inter_nearest',img_near)
img_linear=cv2.resize(img,(int(w*1.5),int(h*1.5)),interpolation=cv2.INTER_LINEAR)
cv2.imshow('inter_linear',img_near)
cv2.waitKey()
cv2.destroyAllWindows()
原图:

1.5倍放大,最近邻差值:

1.5倍放大,双线性差值:

这张图感觉差别不大QAQ
参考
https://blog.csdn.net/weixin_39940512/article/details/105343418
https://blog.csdn.net/qq_37577735/article/details/80041586