Savitsky-Golay滤波器及源码实现

SG平滑算法是由Savizkg和Golag提出来的。基于最小二乘原理的多项式平滑算法，也称卷积平滑。为啥叫多项式平滑呢？且看下去。
　　下面使用五点平滑算法来说明平滑过程
　　原理很简单如图：

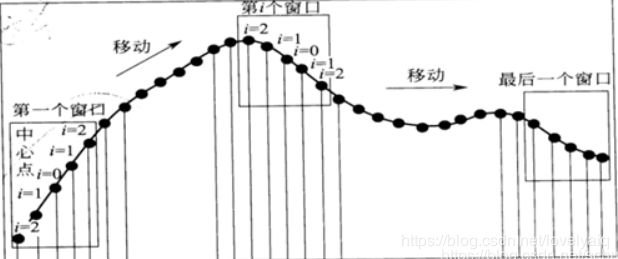
　　把光谱一段区间的等波长间隔的5个点记为X集合，多项式平滑就是利用在波长点为$X_{m-2},X_{m-1},X_m,X_{m+1},X_{m+2}$的数据的多项式拟合值来取代$X_m$,，然后依次移动，直到把光谱遍历完。
　　Savitsky-Golay卷积平滑关键在于矩阵算子的求解。
　　假设滤波窗口的宽度为n = 2m+1, 各测量点x = (-m, -m+1, ,0, , m - 1, m)， 采用k-1次 多项式对窗口内的数据点进行拟合：
$$y=a_0+a_{1}x+a_{2}x+....+a_{k-1}{x}^{k-1}$$
　　于是就有了n个这样的方程，组成k元线性方程组，要使方程组有解，应该满足n大于等于k，一般选择n > k。通过最小二程法拟合确定参数A。由此得到：
$$\left\{\begin{array}{c}{y}_{-m}\\ y_{-m+1}\\ .\\ .\\ .\\ y_m\end{array}\right\}=\left\{\begin{array}{cccc}1& -m& ...& (-m{)}^{k-1}\\ 1& -m+1& ...& (-m+1{)}^{k-1}\\ .& & & \\ .& & & \\ .& & & \\ 1& m& ...& (m{)}^{k-1}\end{array}\right\}\left\{\begin{array}{c}{a}_0\\ a_1\\ .\\ .\\ .\\ a_{k-1}\end{array}\right\}+\left\{\begin{array}{c}{e}_{-m}\\ e_{-m+1}\\ .\\ .\\ .\\ e_m\end{array}\right\}$$
使用矩阵表示：
$$Y_{(2m+1)\ast 1}=X_{(2m+1)\ast k}\ast A_{k\ast 1}+E_{(2m+1)\ast 1}$$
A 的最小二乘解为：
$$A=(X^T\ast X{)}^{-1}\ast X^T\ast Y$$
则Y的滤波值为：
$$Y=X\ast A=X\ast (X^T\ast X{)}^{-1}\ast X^T\ast Y=B\ast Y$$
其中$$B=X\ast (X^T\ast X{)}^{-1}\ast X^T$$
　　所以，我们的目标就是求解B矩阵。
　　这里通过输入二位数组，对每一行进行S-G滤波。并且每行采取最近邻补齐，所有的补齐方式如下，读者可以自行实现其他方式。

        mode       |   Ext   |         Input          |   Ext
        -----------+---------+------------------------+---------
        'mirror'   | 4  3  2 | 1  2  3  4  5  6  7  8 | 7  6  5
        'nearest'  | 1  1  1 | 1  2  3  4  5  6  7  8 | 8  8  8
        'constant' | 0  0  0 | 1  2  3  4  5  6  7  8 | 0  0  0
        'wrap'     | 6  7  8 | 1  2  3  4  5  6  7  8 | 1  2  3

在计算矩阵时，使用了Opencv矩阵，例如求矩阵转置和求逆

定义S-G滤波函数

需要注意的是，order必须要比滑动窗口要小，且滑动窗口不能为偶数。

void SavitskyGolaySmoothing(float *arr,int window_size, int order, int rows, int cols){
    if(window_size % 2 == 0){
        throw std::logic_error("only odd window size allowed");
    }
    if(order >= window_size){
        throw std::logic_error("Order must < window_size");
    }

    cv::Mat A = cv::Mat::zeros(window_size, order, CV_32FC1);
    cv::Mat A_T, A_INV, B;
    cv::Mat kernel;
    cv::Mat result = cv::Mat::zeros(window_size, 1, CV_32FC1);

    int step = int((window_size - 1)/2);
    for(int i = 0; i < window_size; i++){
        for(int j = 0 ; j < order; j++){
            float x = pow(-step + i, j);
            A.at(i,j) = x;
        }
    }
    A_T = A.t();
    A_INV = (A_T * A).inv();
    B = A * A_INV * A_T;

    B.row(step).copyTo(kernel);

    float *wrap_data = new float[step*2 + cols];
    for(int row =0; row < rows; row++){
        //Extend start data, size is step
        for(int n = 0; n < step; n++)
        {
            wrap_data[n] = arr[row * cols];
        }
        //Copy input data
        for(int col =0; col < cols; col++){
            wrap_data[col + step] = arr[row * cols + col];
        }
        //Extend end data, size is step
        for(int n = 0; n < step; n++){
            wrap_data[cols  + step + n] = arr[row * cols + cols -1];
        }
        for(int m = step; m < step + cols; m++){

            for(int n = -step, j = 0; n <=step; n++, j++){
                result.at(0, j) = wrap_data[m + n];
            }

            arr[row * cols + m - step] = cv::Mat(kernel * result).at(0 ,0);
        }
    }
    delete []wrap_data;

}

随机输入一组数据，并将结果打印处理，从结果可以看出，滤波后的数据比较平滑。

    float c[1][18] = {2, 2, 5, 2, 1, 0, 1, 4, 9,2, 2, 5, 2, 1, 0, 1, 4, 9};
    SavitskyGolaySmoothing((float*)c, 5, 3, 1, 18);
    for(int row = 0; row < 1; row++){
        for(int col; col < 18; col++){
            swtd::cout<

输出结果为：

1.74286
3.02857
3.54286
2.85714
0.657143
0.171428
1
5.2
6.17143
3.97143
2.42857
3.54286
2.85714
0.657143
0.171428
1
4.6
7.97143

为验证S-G滤波准确性，在python下基于scipy库进行仿真。

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import savgol_filter

Size = 100

x = np.linspace(1, Size,Size)

data = np.random.randint(1, Size, Size)

plt.plot(x, data)
print(data)
y = savgol_filter(data, 5, 3, mode= 'nearest')
# print(x)
plt.plot(x, y, 'b', label = 'savgol')
arr = []
window_size = 5
order =3
step = int((window_size-1)/2)
for i in range(window_size):
    a = []
    for j in range(order):
        y_val = np.power(-step + i, j)
        a.append(y_val)
    arr.append(a)

arr = np.mat(arr)
print(arr)
arr = arr * (arr.T * arr).I * arr.T
# print(arr)
# print(step)
a = np.array(arr[step])
a = a.reshape(window_size)
# print(a.shape)


data = np.insert(data, 0, [data[0] for i in range(step)])

data = np.append(data, [data[-1] for i in range(step)])

list = []
for i in range(step, data.shape[0] - step):
    arra = []
    for j in range(-step, step+1):
        arra.append(data[i +j])

    b = np.sum(np.array(arra) * a)
    # c = arr * (np.mat(arra).reshape(window_size,1))
    # for j in range(window_size):
    #     data[i - step + j] = c[j][0]
    # print(c.reshape(window_size))
    list.append(b)
# print((list))
plt.plot(x, np.array(list), 'r', label = 'result')


plt.legend()
plt.show()

从仿真结果中可以看出，自己写的滤波函数与Scipy自带的savgol_filter结果一致。

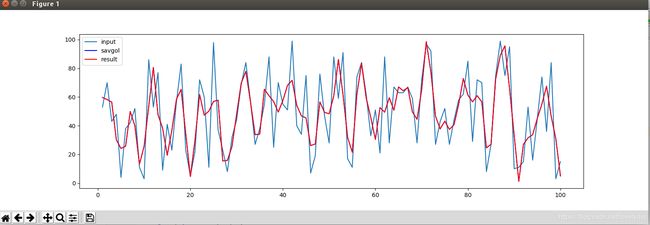
　　这里有一点不明白：为什么savgol_filter输入order为偶数时，它会自动向上加1，例如oder = 4时，滤波结果与oder = 5一致？如果有知道的大神，请赐教。