学习之2——线性规划问题的MATLAB实现

1.Matlab规定线性规划的标准形式为： 
 
几个不等式是问题的约束条件，记为 s.t.(即 subject to)。 MATLAB中求解线性规划的命令为： 
[ x，fval ]=linprog（f，A，b） 
[ x，fval ]=linprog（f，A，b，Aeq，beq） 
[ x，fval ]=linprog（f，A，b，Aeq，beq，lb，ub） 
其中：返回的x为决策向量的取值； 返回的fval是目标函数的最大值；f为价值向量，即这里的c的转置；A和b对应的是线性不等式约束；Aeq和beq对应的是线性等式约束；lb和ub分别对应的是决策向量的下界向量和上界向量。

eg： 

 
(1)化为Matlab标准型，即 
 

(2)求解的Matlab程序如下：

f=[-2,-3,5]'
A=[-2,5,-1;1,3,1];  b=[-10;12];
Aeq=[1,1,1];    beq=7;
[x,fval]=linprog(f,A,b,Aeq,beq,zeros(3,1));
x
fval=-fval

这里的zeros(3,1)是为了产生3行1列的全0矩阵，对应着x1,x2,x3均大于等于0的约束条件。 
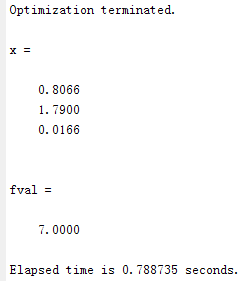
得出结果如下如所示： 

2.可以转化为线性规划的问题 

(1) 

可进一步把模型改写为： 

eg： 
 
做变量变换 

并把新变量重新排列成一维向量 
 
即可把模型变换为线性规划模型，其中：

(2) 
计算的MATLAB程序如下所示：

c=[1:4];c=[c,c]';
a=[1,-1,-1,1;1,-1,1,-3;1,-1,-2,3]; a=[a,-a];
b=[-2;-1;1/2];
[y,fval]=linprog(c,a,b,[],[],zeros(8,1));
x=y(1:4)-y(5:8)
得出的结果如下图所示： 

线性规划在Matlab中的基本函数形式是：linprog(c,A,b)，函数的返回的向量x，其中c代表目标函数的系数，是一个列向量；A代表不等式约束方程参数的系数，b代表约束方程由常数构成的向量。 
线性规划函数：[x,fval]=linprog(c,A,b,Aeq,Beq,LB,UB,X0,Options)：其中Aeq和Beq代表等式约束Ax=b；LB，UB分别是变量X的上下界，X0是X的初始值，Options代表控制参数。 

eg1：

min z=2*x1+3*x2+x3 
Subject to： 
x1+4*X2+2*X3>=8 
3*X1+2*X2>=6 
x1>=0 
x2>=0 
x3>=0 

c = [2;3;1];
a = [1,4,2;3,2,0];
b = [8;6];
A = -a; b = -b;
[x,fval] = linprog(c,A,b,[],[],zeros(3,1)) % zeros(3,1)所有决策变量x1,x2,x3均大于等于0的约束条件

eg2：

min z=-5*x1-4*x2-6*x3 
subject to: 
x1-x2+x3<=20 
3*x1+2*x2+4*x3<=42 
3*x1+2*x2<=30 
0<=x1 
0<=x2 
0<=x3 

c = [-5;-4;-6];
A = [1,-1,1;3,2,4;3,2,0];
b = [20;42;30];
[x,fval,exitflag,output,lambda] = linprog(c,A,b,[],[],zeros(3,1))

eg3：

max=2*x1+3*x2-5*x3   要转成matlab标准形式min
subject to: 
x1+x2+x3=7 
2*x1-5*x2+x3>=10 
x1>=0 
x2>=0 
x3>=0 

c = [2;3;-5];
A = [-2,5,-1];
b = -10;
Aeq = [1,1,1];
beq = 7;
[x,fval] = linprog(-c,A,b,Aeq,beq,zeros(3,1))
value = c'*x     % 求解最佳值
fval = -fval