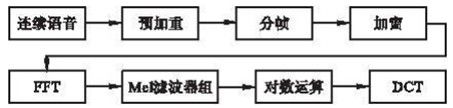
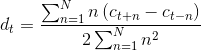语音识别MFCC系列(四)——MFCC特征参数提取
最好先看下下面三篇(其中系统的讲述了离散傅里叶变换,能量密度谱为什么是DFT系数的平方除以总点数,为什么512点的离散傅里叶变换只选前257个分量,离散余弦变换,为什么采样频率要大于真实信号最大频率的两倍,频谱混叠,频谱泄露,为什么要用窗函数等等),做知识储备,如果上述问题不懂,一定要去看哦,都可以找到答案。然后MFCC的提取过程就特别好理解。因为我就是这么学过来的!本文是我看了代码以后做的总结,我觉得这篇总结有些东西写的不清楚,就参考这个改的。
语音识别MFCC系列(一)——连续信号、傅里叶变换
语音识别MFCC系列(二)——离散信号、离散傅里叶变换
语音识别MFCC系列(三)——离散余弦变换DCT
一、数据准备
格式为.wav的音频文件,可以从这里下载,.wav文件存储的是录音设备按固定频率采取的真实声波的某个点。
采样频率一般为8000Hz和16000Hz,采样频率需要大于真实信号最大频率的2倍,才不会导致频谱混叠。比如声卡采样率是8000HZ,那么可以认为原始信号的最大频率处是4000HZ,注意,原始信号的源头是声带一张一合把肺部气体排出,这一张一合的频率叫做基音频率(声音波由3个阶段,声带发出的基音频率是第一阶段;第二阶段是气体声波经过长约17cm的声道,据说第二阶段作为声音音色音质以及文本无关声纹识别中的重要部位,也是共振峰产生的场所;第三阶段是唇口鼻舌,这些部位影响声音的发音,比如元音辅音等),为了理解清晰,原始信号的频率可以默认为是声带一张一合的频率,而声卡采样频率则是1秒钟采取多少个点,所以这两者有本质的区别,但都是频率。
使用python(scipy和numpy库)的(rate,signal) = scipy.io.wavfile.read("Ansel.wav"),读取信号signal = [ 0 0 -1 ..., 627 611 702],这是个含有107000个元素的数组,还可以得到该声音文件的采样频率,此处频率rate=8000Hz。
二,预加重,{A(1*107000)}
个人理解为,由于声带和嘴唇的效应,人的发音系统会抑制语音信号的高频部分,那么低频段能量大,高频段能量小,高频部分的幅值会比较小,高频部分的信噪比(信号幅值/噪音幅值)比较小,换言之,你能从一堆茂密高大的杂草里找到你种的那根正品草吗!预加重就是解决这些问题的,相当于高通滤波器,提高高频部分啦。
![]()
一般![]() 取值为0.95/0.97。
取值为0.95/0.97。
做法:signal = [ 0 0 -1 ..., 627 611 702]含有107000个点,针对这些点,套用公式signal[i]=signal[i+1]-0.97*signal[i],得到一个新的数组A=[ 0. 0. -1. ..., -40.36 2.81 109.33],数组大小还是107000。
三,分帧,{B(1336*200)}
分帧原理就不说了,做法:把上述数组A的元素值,200个为一帧,80个为帧移,总共可以得到1336帧,因为不是整除,1336*80+200=107080,多出的80个点用0填补,所以得到1336*200的二维数组B。
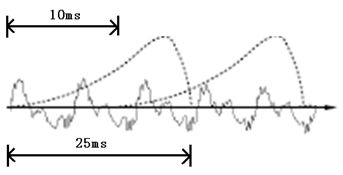
上述200个为一帧,80个为帧移是这样来的,因为默认语音信号具有短时平稳性,这平稳性不是说短时采样得到的值相等,而是认为短时间内声带、声道、唇口鼻腔这3个声音信号源头具有平稳性,据说是人体肌肉活动短时平稳。短时默认是0.025s,两个相邻短时间隔默认是0.01s,因为我分析的.wav文件是8000HZ, 所以0.025s内有0.025*8000=200个采样点,帧移0.01*8000=80个采样点。
四,加窗,{C(1336*200)}
汉明窗函数是一个余弦函数,作用是为了缓解频率混叠,接下来说下具体怎么加窗。设一帧内信号是![]() ,则乘上汉明窗后为
,则乘上汉明窗后为![]() ,其中汉明窗为:
,其中汉明窗为:
![]()
不同的a产生不同的汉明窗,通常a取0.46。我们根据上式得到一个1336*200的窗数组C。分帧后的数组B和窗函数数组C具有相同的维度,把它们对应位置的元素值相乘,即可以得到加窗后的二维数组C,C[i[j]=B[i][j]*C[i][j]]。
五,离散傅里叶变换(DFT),{D(1336*257),E(1336*257),F(1336*1)}
已知经过加窗后的信号C具有1336*200维,也就是说有1336行(帧),每行200个点,每相邻两行之间有120个重合点(帧移80)。那么对它做DFT,做法:对有1336帧,每一帧都作N=512的DFT(N为2的幂次方可做快速傅里叶变换),得到257个频率分量。得到1336*257维的频域信号D,帧数还是1336,对每一帧的257个点的值(个人认为是振幅)取平方,再乘以1/512,便得到1336*257的能量密度谱,然后对每一帧的257个能量值简单相加,得到该帧的能量总值,一共有1336帧,于是有1336个能量总值,即拥有1336个元素值,记为数组F,数组中每个元素值代表一帧的能量总值。
六,获得梅尔滤波器{G(26*257)}
![]()
如上图,梅尔值是一个新的量度,相比频率量度,梅尔更接近人耳的听觉机理,通俗的说,就像纳米和米一样,如果我们用纳米衡量我们身边的事物会是一种什么感受?所以频率![]() 的某一个值对应着梅尔的某一个值
的某一个值对应着梅尔的某一个值![]() ,该映射关系可以用下式描述:
,该映射关系可以用下式描述:
![]()
我们看第一个公式,我们的采样频率除以2就是真实信号的最大频率,真实信号的最小频率为0,依据公式的单调性,我们以这个最大频率和最小频率为界限分别得到梅尔刻度的最大最小值,可以把信号的所有频率值刻画在这个梅尔区间之内。梅尔滤波器个数一般默认26个,在上述最大最小梅尔区间等间距插入26个值,包括边界,就是28个梅尔值![]() ,算出对应28个频率值
,算出对应28个频率值![]() 。接下来对这28个频率值,依次代入公式
。接下来对这28个频率值,依次代入公式
便可以得到28个k值,k位于0-256。512是傅利叶变换的N,8000是采样频率。这个式子是把频率对应到频谱中257个频率分量的某个,比如说之前算的![]() 是2000,而257个频率分量的第200个频率是2000,那求出的k就是200。
是2000,而257个频率分量的第200个频率是2000,那求出的k就是200。
![]()
三角滤波器如上图所示,横坐标是0-256,频率响应定义为:
上式中的![]() 代表第几个滤波器,
代表第几个滤波器,![]() 为横坐标0-256。26个滤波器就是算257个频率分量分别属于26个频率带的概率,举个不严密例子哈,第一个滤波器的频率带是0-10,那么第250个频率分量很明显不属于这个频率带,那这个概率就是0,那第5个频率分量很明显位于频率带的中心,那这个概率就是1。接下来根据上式计算26个滤波器的二维数组,也就是26*257二维数组G。
为横坐标0-256。26个滤波器就是算257个频率分量分别属于26个频率带的概率,举个不严密例子哈,第一个滤波器的频率带是0-10,那么第250个频率分量很明显不属于这个频率带,那这个概率就是0,那第5个频率分量很明显位于频率带的中心,那这个概率就是1。接下来根据上式计算26个滤波器的二维数组,也就是26*257二维数组G。
七,得到能量特征参数的和能量总值{H(1336*26)}
因为我们上一步已经算出257个频率分量分别属于26个频率带的概率(这里有点像模糊聚类啦),那我们就按这个概率乘以频率分量对应的能量相加,就是算出26个频率带对应的能量啦!为什么呢,因为人耳可能分辨不出相差很小的频率,就是说一个频率带的听起来没差,那我们就不需要那么细致的算每个分量的能量,而只要算出每个频率带的能量即可!
做法:把第五步得到的二维矩阵能量谱E(1336*257),乘以第六部的二维数组梅尔滤波器G(26*257)的转置,矩阵的转置可得到257*26的矩阵,然后满足矩阵乘法定律,得到参数H=E*G.T,此处的H其实是1336*26的二维矩阵。
还有个参数是第五步计算出来的每帧能量总值F(1336*1),即拥有1336个元素值的一维数组F。
八,作自然对数运算,离散余弦变换(DCT)和升倒谱运算{J(1336*13),K(13*1),L(1336*13),feat[1336*13]}
对H的每一个元素值做ln运算,即H[i][j]=ln(H[i][j]),据说是因为人耳听到的声音大小和信号本身的大小是幂次方关系,所以要求个对数。接着对feat的每一行做DCT。因为大部分信号数据一般集中在变换后的低频区,所以对每一帧只取前13个数据就好了,于是得到1336*13的二维数组J。
针对1336*13的二维数组J做升倒谱操作(升倒谱我不懂),默认升倒谱系数为22,这个过程做法是先产生一个拥有13个元素的一维数组K,这13个元素的值K[i]=1+(22 /2)*sin(pi*i/22),其中22是升倒谱系数,pi是圆周率3.1415926。得到这个数组K之后,针对1336*13的二维数组J,J[i][j] = J[i][j]*K[j],得到1336*13的二维数组L,这其实就是mfcc参数的第一组。如果这组参数想要加上能量作为其表示方式,可以把这1336帧,也就是每一行的的第一个元素用一维数组F的每个值替换,即L[i][0] = F[i]。
我们把这经过错综复杂得到的L记为feat,它是个二维数组,拥有1336*13个值,这也是mfcc参数的基础参数,也是第一组,默认是有3组,接下来计算第二和第三组参数。
九,计算第二组和第三组参数{feat[1336*13],feat'[1336*13],feat''[1336*13]}
第二组参数其实就是在已有的基础参数下作一阶微分操作,第三组参数在第二组参数下作一阶微分操作,这里的微分采用下式,这个式子来自何强,何英的“Matlab扩展编程”一书:
其中![]() 为第几帧,
为第几帧,![]() 为该帧前后第几个,
为该帧前后第几个,![]() 为
为 ![]() 的最大值,一般取2。
的最大值,一般取2。
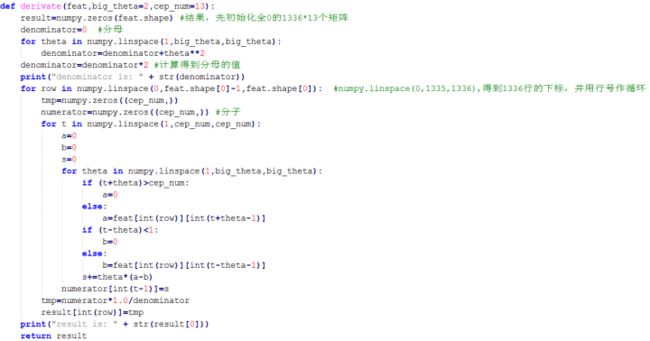
做法:抽取一个计算一阶微分的函数,然后把1336*13的二维数组feat作为参数传入,返回feat的一阶微分feat‘,feat'同样有1336*13个元素值。其实这个过程是把feat按照行作循环,每一行拥有13个元素值,如果不考虑边际效应,feat'[i][j]={feat[i+1][j]-feat[i-1][j] + 2(feat[i+2][j]-feat[i-2][j]) + 3(feat[i+3][j]-feat[i-3][j]) + ... + n(feat[i+n][j]-feat[i-n][j])} / M,M作为分母,是这个函数输入的big_theta来决定的,big_theta默认值是2,此处的M值可以算出是10,过程参照函数代码。最后得到的输出是1336*13的二维数组feat',也是mfcc参数的第二组参数。
第三组参数同上,把feat'作为参数运用抽取出来的函数作计算,得到输出记为feat'',feat''二维数组同样有1336*13个元素值,这是mfcc参数的第三组参数。
十,得到最后输出{mfcc(1336*39)}
由前八步和第九步,可以得到feat,feat'和feat'',这3个参数都是拥有1336*13个元素值的二维数组,而且这三个二维数组的每一行第一个元素值可以根据需要,用该行(帧)的能量总值替换。把feat,feat‘和feat''拼在一起,即基于feat,每一行横向追加feat'和feat''每行的元素值,得到拥有1336*39个元素值的一个二维数组,也就是mfcc系数,这就是最后得到的结果。
得到的mfcc系数,可供语音识别或声纹识别(文本无关,文本相关)等技术,但语音识别需要语料库,因此还需要建立语音模型来训练语音,经典的语音模型有HMM,新兴的有神经元模型。
参考网址:https://zhuanlan.zhihu.com/p/27416870
http://practicalcryptography.com/miscellaneous/machine-learning/guide-mel-frequency-cepstral-coefficients-mfccs/#computing-the-mel-filterbank
https://haythamfayek.com/2016/04/21/speech-processing-for-machine-learning.html
https://blog.csdn.net/TH_NUM/article/details/80597495
https://blog.csdn.net/shichaog/article/details/72809261
https://my.oschina.net/zzw922cn/blog/533175