二维离散傅里叶变换与逆变换的原理与实现(Matlab)

前言

在野外数据采集中，虽然单个仪器采集的是一维信号，但是当把多台仪器数据汇总并生成做二维剖面的图像时，噪声可不只有一维的，更有x,y两个方差同时存在的"二维噪声"！我们已经知道一维噪声可以用一维傅里叶变换到频域滤波，同理二维噪声也可以用二维傅里叶变换到"频率滤波"。

二维傅里叶正变换的原理

笔者很讨厌一上来就看到一连串复杂的公式！因此当我看懂一个原理后，我就会用最好理解的方式来重述它，毕竟我更偏重于应用。二维傅里叶变化，只用一个公式：

公式1：二维傅里叶变换公式(其实不用看它)
公式中参数说明：

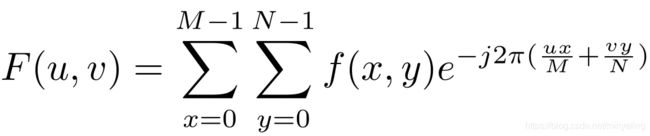
公式(1)
公式中参数说明：
M、N分别是图像的长和宽；
u、x范围从1到M-1；v、y范围从1到N-1。
公式看上去不难，但其实还是不太明确到底怎么用啊！它其实可以矩阵相乘的形式表示：

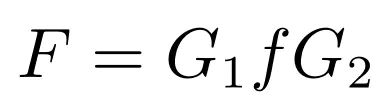
公式(2)
公式2中f是原始二维数据矩阵，G_{1}和G_{2}分别是如下：

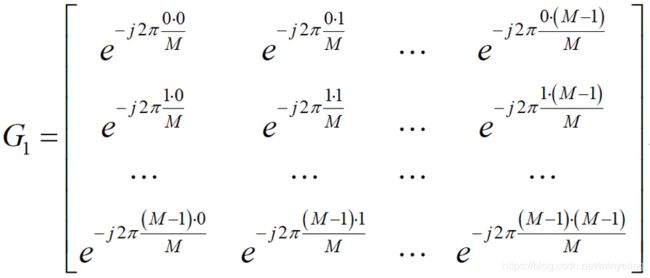
公式(3)

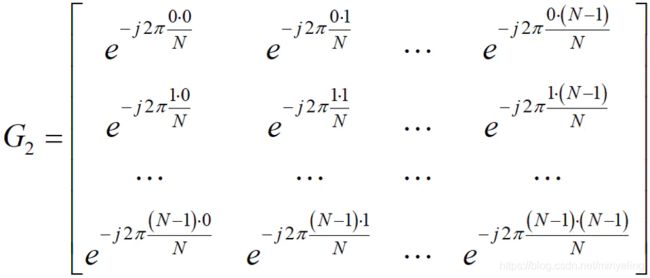
公式(4)
这用Matlab太好实现了叭！G_{1}和G_{2}这么有规律，很容易就编程出来了~ 然后3个矩阵做个乘积，就换到频率域了！二维傅里叶变换就结束了！

二维傅里叶反变换

定义的公式为公式5(不用看)，矩阵形式的公式为公式6(看这个即可)：

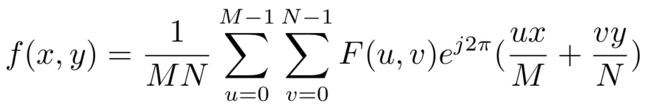
公式5：二维傅里叶反变换公式

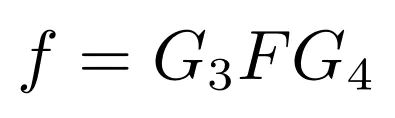
公式6：矩阵形式(看这个)
其中G_{3}和G_{4}矩阵为：

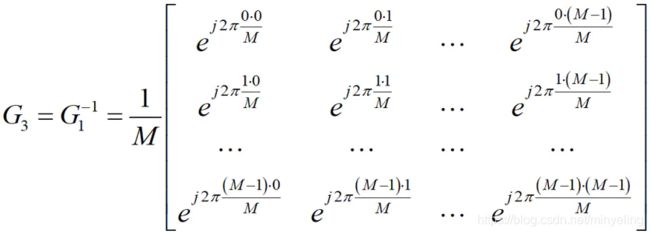
公式(7)

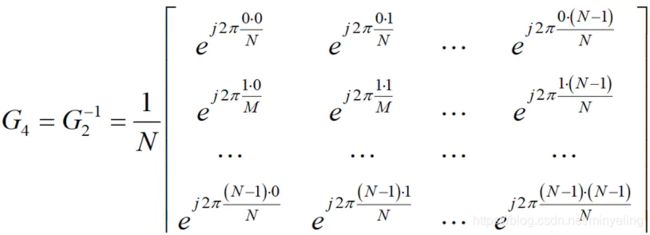
公式(8)
到此，二维傅里叶逆变换也结束了！整个二维傅里叶变换就都结束了！真的很简单！下面我们就在Matlab中手写实现正、逆这两个过程。

Matlab程序实现

首先实现正变换程序，对应Matlab自带函数为：fft2

clc; clear;

data = imread('zxc.jpg');  % 数据——最好比卷积核的尺寸大
data = im2double(data); 
data = rgb2gray(data);     % rgb转为灰度图像
subplot(1,3,1);
imshow(data);
title('原始图像')

zidai = fft2(data);   % matlab自带函数，来用对比
subplot(1,3,2);
imshow(real(zidai));  % 一般只要实部
title('自带的fft2生成的"频域"图像');

size_data = size(data);
M = size_data(1);  % 图(原始数据矩阵)的长
N = size_data(2);  % 图(原始数据矩阵)的宽

% 下面是傅里叶正变换必备的一些矩阵:
Wm = exp(-j*2*pi/M);
Wn = exp(-j*2*pi/N); % 不同G中用不同的W
Em = zeros(M);
En = zeros(N);     % E是辅助计算矩阵
Gm = zeros(M)+Wm;
Gn = zeros(N)+Wn;  % G是计算时要用的矩阵
F = zeros(M,N);    % F是转换到频域的结果

% 对Gm的计算: 循环长度为M
fprintf('二维离散傅里叶变换开始:\n');
for row = 0:M-1
    for col = 0:M-1
        Em(row+1,col+1) = row * col;
        Gm(row+1,col+1) = Gm(row+1,col+1)^Em(row+1,col+1);
    end
end
% 对Gn的计算: 循环长度为N
for row = 0:N-1
    for col = 0:N-1
        En(row+1,col+1) = row * col;
        Gn(row+1,col+1) = Gn(row+1,col+1)^En(row+1,col+1);
    end
end

F = real(Gm*data*Gn);  % F = Gm*f*Gn是计算公式，一般只要实部
subplot(1,3,3);
imshow(F);
title('手写的myfft2生成的"频域"图像');

error = sum(sum((real(F)-real(zidai)).^2));
if error < 10^(-10)
    fprintf('自带与手写结果一致!\n');
else
    fprintf('不一致!\n');
end

接着正变换结果(把频域结果当输入)逆变换程序如下，对应Matlab自带函数：ifft2

% 鉴于正向fft2手写与自带结果一致；
% ifft2的输入就直接用自带的fft2的结果。
clc; clear;

data = imread('zxc.jpg');  % 数据——最好比卷积核的尺寸大
data = im2double(data); 
data = rgb2gray(data);     % rgb转为灰度图像
subplot(1,3,1);
imshow(data);
title('原始图像')

F = fft2(data);
subplot(1,3,2);
imshow(real(F));  % 一般画图只要实部, 作为输入时实虚都要！！
title('自带的fft2生成的"频域"图像');

% s = ifft2(F);
% subplot(1,3,3);
% imshow(s);
% return;

size_data = size(F);
M = size_data(1);  % 图(原始数据矩阵)的长
N = size_data(2);  % 图(原始数据矩阵)的宽

% 下面是傅里叶逆变换必备的一些矩阵:
Wm = exp(-j*2*pi/M);
Wn = exp(-j*2*pi/N);  % 不同G中用不同的W
Em = zeros(M);
En = zeros(N);        % E是辅助计算矩阵
Gm = zeros(M)+Wm;
Gn = zeros(N)+Wn;  % G是计算时要用的矩阵
f = zeros(M,N);    % F是转换到频域的结果

% 对Gm的计算: 循环长度为M
fprintf('二维离散反傅里叶变换开始:\n');
for row = 0:M-1
    for col = 0:M-1
        Em(row+1,col+1) = -row * col;
        Gm(row+1,col+1) = Gm(row+1,col+1)^Em(row+1,col+1);
    end
end
Gm = Gm/M;
% 对Gn的计算: 循环长度为N
for row = 0:N-1
    for col = 0:N-1
        En(row+1,col+1) = -row * col;
        Gn(row+1,col+1) = Gn(row+1,col+1)^En(row+1,col+1);
    end
end
Gn = Gn/N;   % 注意：这个/N和上面的/M都是算完G之后才除以的！因为上面计算的时候是幂项变化！

f = real(Gm*F*Gn);  % f = Gm*F*Gn是计算公式，一般只要实部
subplot(1,3,3);
imshow(f);
title('手写的myidft2生成的"原始"图像');

error = sum(sum((real(f)-real(data)).^2));
if error < 10^(-10)
    fprintf('反变换后与原图一致!\n');
else
    fprintf('不一致!\n');
end