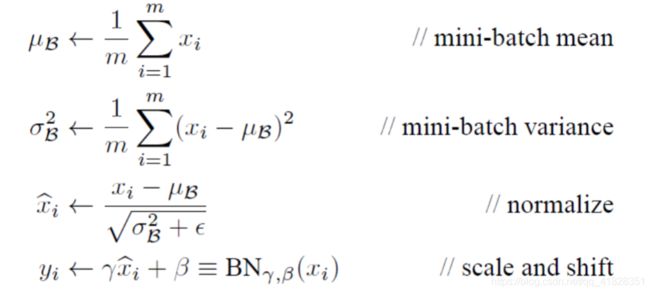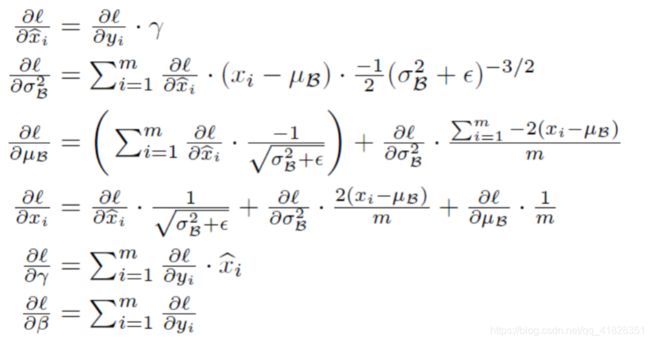cs231n assignment(二) 多层神经网络以及反向传播的代码推导

目录

序

多层全连接神经网络搭建

（1）、input -> (affine_forward) -> out* -> (relu_forward) -> out ，全连接和relu激活

（2）、batch-normalization 批量归一化

   3、随机失活（DropOut）

（4）、任意深度神经网络

神经网络优化 - 针对训练过程中的梯度下降

1、SGD with momentum

2、RMSProp

3、Adam

---

序

       原来都是用的c++学习的传统图像分割算法。主要学习聚类分割、水平集、图割，欢迎一起讨论学习。

       刚刚开始学习cs231n的课程，正好学习python，也做些实战加深对模型的理解。

       课程链接

       1、这是自己的学习笔记，会参考别人的内容，如有侵权请联系删除。

       2、代码参考WILL 、杜克，但是有了很多自己的学习注释

       3、有些原理性的内容不会讲解，但是会放上我觉得讲的不错的博客链接

       4、由于之前没怎么用过numpy，也对python不熟，所以也是一个python和numpy模块的学习笔记

       5、本文参考参考

       本章前言：本章实现了多层全连接的神经网络和优化算法的使用，比如批量归一化、SGD+Momentum、Adam等，本章重点：反向传播以及优化算法

       在jupyter中写的代码，要import需要下载成为.py文件，import之后如果.py文件中的内容有了修改需要重新打开jupyter，很麻烦，现在在import之后加上以下代码，更改.py文件后就不需要重新打开jupyter了。

#自动加载外部模块
%reload_ext autoreload
%autoreload 2

---

多层全连接神经网络搭建

       之前实现的是一个两层的神经网络，结构为 input -> hidden ->relu -> score -> softmax - output。层数较少，给出的推导是从后往前一步一步推导，这在多层神经网络中是不太现实的，层数变多，一层一层推太过于麻烦。在实际过程中，往往采用模块化的反向传播推导。

       多层全连接神经网络结构将会被模块化分割：

（1）、input -> (affine_forward) -> out* -> (relu_forward) -> out ，全连接和relu激活

接下来是实现向前传播代码：

def affine_forward(x,w,b):
    out = None
    x_reshape = np.reshape(x,(x.shape[0],-1))
    out = x_reshape.dot(w) + b 
    cache = (x,w,b)
    return out,cache     #返回线性输出，和中间参数（x,w,b）


def relu_forward(x):
    out = np.maximum(0,x)
    cache = x     #缓存线性输出a
    return out,cache


#模块化
def affine_relu_forward(x,w,b):
    a,fc_cache = affine_forward(x,w,b)   #a是线性输出，fc_cache中存储（x,w,b)
    out,relu_cache = relu_forward(a)     #relu_cache存储线性输出a
    cache = (fc_cache,relu_cache)        #缓冲元组：（x,w,b,(a)）
    return out,cache                     #返回激活值out 和参数（x,w,b,(a)）

既然有了向前传播模块，那就得有反向传播模块：

def affine_backward(dout,cache):
    """
    输出层反向传播
    dout 该层affine_forward正向输出数据out的梯度，对应softmax_loss/relu中的输出dz
    cache 元组，正向流入输入层的数据x，和输出层的参数（w，b）
    """
    z,w,b = cache    #z为上一层的激活值，也是本层的输入
    dx,dw,db = None, None,None
    x_reshape = np.reshape(z, (z.shape[0],-1))
    dz = np.reshape(dout.dot(w.T),z.shape)    #参考公式
    dw = (x_reshape.T).dot(dout)              #参考公式
    db = np.sum(dout,axis=0)                  #参考公式
    return dz,dw,db

def relu_backward(dout,cache):    #传入的是
    """
    relu激活，小于0的梯度为0，大于0的梯度为1
    """
    dx,x = None, cache
    dx = (x>0) * dout
    return dx

def affine_relu_backward(dout,cache):
    fc_cache, relu_cache = cache    #relu_cache 存储线性输出a
    da = relu_backward(dout,relu_cache)    #计算关于relu的梯度，这边是一个复合函数，z=relu（a），a=w1x+b1 -> dz /dx = dz/da *da/dx
    dx,dw,db = affine_backward(da,fc_cache)
    return dx,dw,db

（2）、batch-normalization 批量归一化

       据说，批量归一化可以减小随机初始化权重的影响，加速收敛，学习率适当增大，减少过拟合，使用较低的dropout，减小L2正则化系数等优点。

首先对输入数据进行归一化，使数据的特征均值为0，方差为一，也就是服从标准高斯分布。然后对该数据进行变换重构，使其能后恢复原来的特征分布。

       那现在的神经网络结构就变成了：input -> affine_forward -> BN(batch_normlize) -> relu_forward，也就是在全连接之后加上BN，然后进行激活输出。

#批量归一化（加速收敛，学习率适当增大，加快寻，减少过拟合，使用较低的dropout，减小L2正则化系数）
def batchnorm_forward(x,gamma,beta,bn_param):
    mode = bn_param['mode']
    eps = bn_param.get('eps',1e-5)          #防止除以0
    momentum = bn_param.get('momentum',0.9) 
    
    N,D = x.shape            #N样本个数，D特征个数
    #移动均值和方差，会随着train过程不断变化
    running_mean = bn_param.get('running_mean',np.zeros(D, dtype = x.dtype))
    running_var = bn_param.get('running_var',np.zeros(D, dtype = x.dtype))
    
    out,cache=None,None
    if mode =='train':
        sample_mean = np.mean(x,axis=0)
        sample_var = np.var(x,axis = 0)
        x_hat = (x-sample_mean)/(np.sqrt(sample_var+eps))
        
        out = gamma*x_hat +beta
        cache = (x,sample_mean,sample_var,x_hat,eps,gamma,beta)
        running_mean = momentum*running_var + (1-momentum)*sample_mean
        running_var = momentum*running_var+(1-momentum)*sample_var
    elif mode == 'test':
        out = (x-running_mean)*gamma/(np.sqrt(running_var+eps))+beta
    else:
        raise ValueError('invalid forward batchnorm mode "%s"' %mode)
    
    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var
    
    return out,cache   #cache(线性输出，均值，方差，归一化值，eps，gamma，beta)   #out 变换重构的值


def affine_bn_relu_forward(x,w,b,gamma,beta,bn_param):
    a,fc_cache = affine_forward(x,w,b)
    a_bn, bn_cache = batchnorm_forward(a,gamma,beta,bn_param)  #BN层
    out,relu_cache = relu_forward(a_bn)    #将归一化后的值激活，relu_cache中缓存变换重构值
    cache = (fc_cache,bn_cache,relu_cache)
    return out,cache

有了向前传播自然要有反向传播：其实我也没看公式，直接抄的代码......因为反向传播的链式求导原理是一样的

def batchnorm_backward(dout,cache):
    x,mean,var,x_hat,eps,gamma,beta = cache
    N = x.shape[0]
    dgamma = np.sum(dout*x_hat,axis=0)
    dbeta = np.sum(dout*1, axis=0)
    dx_hat = dout*gamma
    dx_hat_numerator = dx_hat/np.sqrt(var +eps)
    dx_hat_denominator = np.sum(dx_hat * (x-mean),axis=0)
    dx_1 = dx_hat_numerator
    dvar = -0.5*((var+eps)**(-1.5))*dx_hat_denominator
    dmean = -1.0*np.sum(dx_hat_numerator,axis = 0)+dvar*np.mean(-2.0*(x-mean),axis=0)
    dx_var = dvar*2.0/N*(x-mean)
    dx_mean =dmean*1.0/N
    dx = dx_1+dx_var+dx_mean
    
    return dx,dgamma,dbeta


def affine_bn_relu_backward(dout,cache):
    fc_cache,bn_cache,relu_cache = cache
    da_bn = relu_backward(dout,relu_cache)
    da,dgamma,dbeta = batchnorm_backward(da_bn,bn_cache)
    dx,dw,db = affine_backward(da,fc_cache)
    return dx,dw,db,dgamma,dbeta

（3）、随机失活（DropOut）

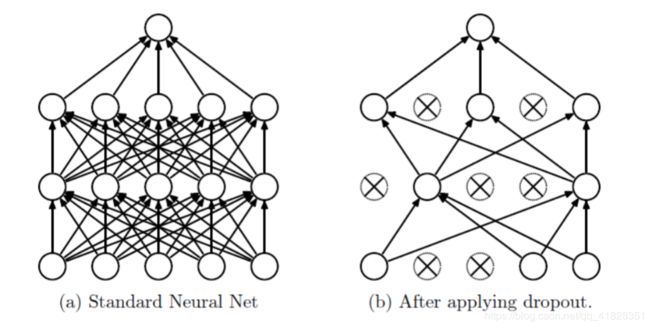
在全连接神经网络中，层数越深，参数越多，测试集的准确率也越来越高，但是在验证集上效果不好，这是因为出现了过拟合。通俗来说，网络为了迎合测试集，提取了过多的特征，而这些特征的作用并没有那么大。随机失活就是随机让神经元失效，也就是某些特征的作用被取消了，这样就达到了一定程度上防止过拟合的能力。

#随机失活
def dropout_forward(x,dropout_param):
    """
    dropout_param p 失活概率
    """
    p,mode = dropout_param['p'],dropout_param['mode']
    if 'seed' in dropout_param:
        np.random.seed(dropout_param['seed'])
        
    mask = None
    out = None
    
    if mode == 'train':
        keep_prob = 1-p 
        mask = (np.random.rand(*x.shape)

反向传播：原理和Relu差不多，随机失活是利用概率掩膜来实现的，掩膜为1不失活，否则失活为0，也就是梯度为1或者为0

def dropout_backward(dout,cache):
    dropout_param,mask = cache
    mode = dropout_param['mode']
    
    dx = None
    if mode == 'train':
        dx = mask * dout
    elif mode == 'test':
        dx = dout
    return dx 

（4）、任意深度神经网络

       所有的模块都被搭建完成，那就可以模块化神经网络了。总共分为三个部分，一个是参数初始化，一个是损失函数计算，还有一个应该是训练。这边暂时只有两个部分

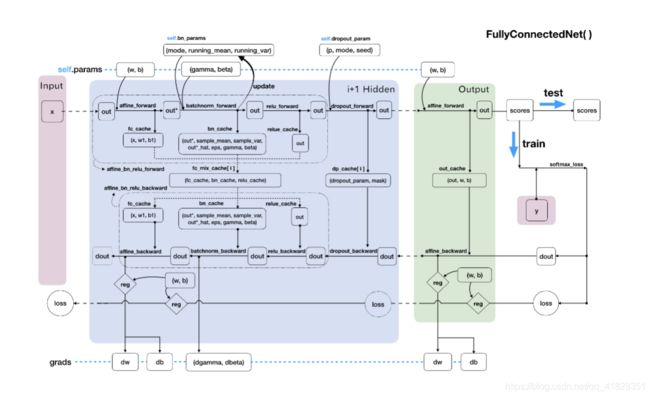
向前传播网络结构(BN，Dropout)： (input ->  BN -> relu -> Dropout) * N(重复N次) -> affine_forward -> softmax -> loss

反向传播(BN，Dropout):  softmax_loss -> affine_backward -> dropout_backward -> (affine_bn_relu_backward) * N

from layers import *
import numpy as np


class FullyConnectedNet(object):
    def __init__(self
                 ,hidden_dims            #列表，元素个数是隐藏层层数，元素值为神经元个数
                 ,input_dim = 3*32*32    #输入神经元3072
                 ,num_classes = 10       #输出10类
                 ,dropout = 0            #默认不开启dropout，（0，1）
                 ,use_batchnorm = False  #默认不开批量归一化
                 ,reg = 0.0              #默认无L2正则化
                 ,weight_scale =1e-2     #权重初始化标准差
                 ,dtype=np.float64       #精度
                 ,seed = None            #无随机种子，控制dropout层
                ):
        self.use_batchnorm = use_batchnorm
        self.use_dropout = dropout>0     #dropout为0，则关闭随机失活
        self.reg = reg                   #正则化参数
        self.num_layers = 1+len(hidden_dims)
        
        self.dtype =dtype
        self.params = {}                 #参数字典
        
        in_dim = input_dim
        #有几个隐藏层，就有几个对应的W，最后输出层还有一个W
        for i,h_dim in enumerate(hidden_dims):
            self.params['W%d' %(i+1,)] = weight_scale*np.random.randn(in_dim,h_dim)
            self.params['b%d' %(i+1,)] = np.zeros((h_dim,))
            if use_batchnorm:
                #使用批量归一化
                self.params['gamma%d' %(i+1,)] = np.ones((h_dim,))
                self.params['beta%d'  %(i+1,)] = np.zeros((h_dim,))
            in_dim = h_dim   #将隐藏层中特征个数传递给下一层
        
        #输出层参数
        self.params['W%d'%(self.num_layers,)] = weight_scale*np.random.randn(in_dim,num_classes)
        self.params['b%d'%(self.num_layers,)] = np.zeros((num_classes,))
        
        #dropout
        self.dropout_param = {}   #dropou参数字典
        if self.use_dropout:      #如果use_dropout为（0，1），启用dropout
            self.dropout_param = {'mode':'train','p':dropout}
        
        if seed is not None:
            self.dropout_param['seed'] = seed
            
        #batch normalize
        self.bn_params = []  #bn算法参数列表
        if self.use_batchnorm:   #开启批量归一化，设置每层的mode为训练模式
            self.bn_params=[{'mode':'train'} for i in range(self.num_layers - 1)]
        
        #设置所有参数的计算精度为np.float64
        for k,v in self.params.items():
            self.params[k] = v.astype(dtype)
    
    
    def loss(self,X,y = None):
        #调整精度
        #X的数据是N*3*32*32
        #Y(N,)
        X = X.astype(self.dtype)
        mode = 'test' if y is None else 'train'
        
        if self.dropout_param is not None:
            self.dropout_param['mode'] = mode
        if self.use_batchnorm:
            for bn_params in self.bn_params:
                bn_params['mode'] = mode
        
        scores = None
        
        
        
        #向前传播
        fc_mix_cache = {}       #混合层向前传播缓存
        if self.use_dropout:    #开启随机失活
            dp_cache = {}       #随即失活层向前传播缓存
            
        out = X
        #只计算隐藏层中的向前传播，输出层单独的全连接
        for i in range(self.num_layers -1):
            w = self.params['W%d'%(i+1,)]
            b = self.params['b%d'%(i+1,)]
            if self.use_batchnorm:
                #利用模块向前传播
                gamma = self.params['gamma%d'%(i+1,)]
                beta = self.params['beta%d'%(i+1,)]
                out,fc_mix_cache[i] = affine_bn_relu_forward(out,w,b,gamma,beta,self.bn_params[i])
            else:
                out,fc_mix_cache[i] = affine_relu_forward(out,w,b)
            if self.use_dropout:
                #开启随机失活，并且记录随机失活的缓存
                out,dp_cache[i] = dropout_forward(out,self.dropout_param)
        
        #输出层向前传播
        w = self.params['W%d'%(self.num_layers,)]
        b = self.params['b%d'%(self.num_layers,)]
        out,out_cache = affine_forward(out,w,b)
        scores = out 
        
        if mode == 'test':
            return scores
        
        #反向传播
        loss,grads=0.0, {}
        #softmaxloss
        loss,dout = softmax_loss(scores,y)
        #正则化loss，只计算了输出层的W平方和
        loss += 0.5*self.reg*np.sum(self.params['W%d'%(self.num_layers,)]**2)
        
        #输出层的反向传播，存储到梯度字典
        dout,dw,db = affine_backward(dout,out_cache)
        #正则化
        grads['W%d'%(self.num_layers,)] = dw+self.reg*self.params['W%d'%(self.num_layers,)]
        grads['b%d'%(self.num_layers,)] = db
        
        #隐藏层梯度反向传播
        for i in range(self.num_layers-1):
            ri = self.num_layers -2 - i  #倒数第ri+1层
            loss+=0.5*self.reg*np.sum(self.params['W%d'%(ri+1,)]**2)    #继续正则化loss
            if self.use_dropout:     #如果使用随即失活，加上梯度下降
                dout = dropout_backward(dout,dp_cache[ri])
            if self.use_batchnorm:   #如果使用BN，加上梯度下降部分
                dout,dw,db,dgamma,dbeta = affine_bn_relu_backward(dout,fc_mix_cache[ri])
                grads['gamma%d'%(ri+1,)] = dgamma
                grads['beta%d'%(ri+1,)] = dbeta
            else:             #否则直接梯度下降
                dout,dw,db = affine_relu_backward(dout,fc_mix_cache[ri])
                #存储到字典中
            grads['W%d'%(ri+1,)] = dw+self.reg * self.params['W%d'%(ri+1,)]
            grads['b%d'%(ri+1,)] = db 
            #返回本次loss和梯度值
        return loss,grads

---

神经网络优化 - 针对训练过程中的梯度下降

1、SGD with momentum

       上面的loss函数输出的是当前的损失值和模型参数的梯度，梯度下降过程中也就是在train的过程中，在负梯度方向上对模型参数进行更新。

       随机梯度下降（SGD）之前使用过，w -= learning_rate * dW

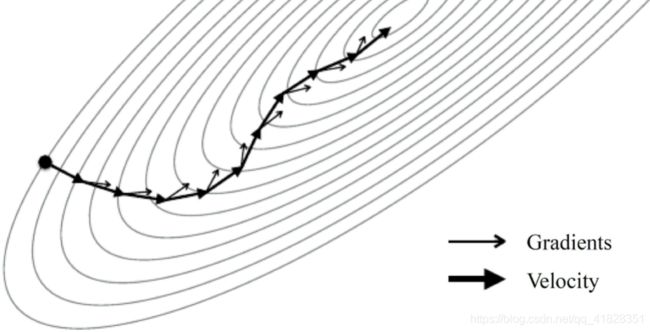
       SGD + momentum （随机梯度下降的动量更新方法）。w0 =  w0*mu - learning_rate*dW个人理解，原本是按照梯度来走，但是现在更新后有了自己的速度，速度不可瞬间变化，把梯度看作一个力，这个力将会概念速度的大小和方向。

def sge_momentum(w,dw,config = None):
    if config is None:
        config = {}
    config.setdefault('learning_rate',1e-2)
    config.setdefault('momentum',0.9)
    v = config.get('velocity',np.zeros_like(w))
    
    next_w = None
    
    v = config['momentum']*v - config['learning_rate']*dw
    next_w = w + v 
    
    config['velocity'] = v 
    return next_w,config

2、RMSProp

3、Adam

---

实例化神经网络及训练

参考链接：课程作业第52页的Solver