语音信号处理 | 使用短时能量和谱质心特征进行端点检测

概述

在复杂的应用环境下，从音频中分割出语音信号和和非语音信号，是一个很重要的环节，因为它不仅可以减少数据以及系统的运行时间，还能够抑制噪声对系统的干扰。端点检测就是判断语音的起点和终点。常用的方法有基于短时能量和过零率的双门限法。

本文将介绍一种基于信号短时能量和谱质心的端点检测方法。

原理及MATLAB实现

基本流程

1. 从语音信号中提取短时能量特征和谱质心特征序列（即对语音信号分帧加窗后，从每一帧中提取上述两个特征，最后将提取的特征组成两个特征序列）
2. 分别为两个特征序列动态地估计一个阈值
3. 利用估计的阈值对这两个特征序列进行阈值判断
4. 根据阈值判断结果提取出语音片段

特征提取

使用短时能量特征和谱质心特征进行端点检测的原因为：

1. 在一些简单的场景中（信噪比较高），语音段的能量比静音段的能量高很多。
2. 如果非语音段包含一些环境的声音，那么语音段的谱质心将会比较大，因为噪声信号往往具有较低的频谱，因此它的谱质心也较小

因此可以用短时能量和谱质心分割出语音段、静音段和噪声段。在进行特征提取之前，需要将语音信号分割成无重叠的短时信号，本文采用的帧长为50ms。

接下来对每一帧信号进行如下处理，从而提取该帧信号的短时能量和谱质心特征

• 短时能量

设$x_i(n),n=1,\cdots ,N$是第$i$帧信号，长度为$N$，通过以下公式计算该帧的能量：
$$E(i)=\frac{1}{N}\sum _{n=1}^N|x_i(n){|}^2$$
这个特征可以用于检测静音帧，也可用于区分音频的种类

提取短时能量序列的MATLAB程序如下：

function E = ShortTimeEnergy(signal, windowLength, step)
%% 计算短时能量
% 输入:
% 	signal		:原始信号
% 	windowLength:帧长
% 	step		:帧移
% 输出:
% 	E			:每一帧的能量
    signal = signal / max(max(signal));
    curPos = 1;
    L = length(signal);
    numOfFrames = floor((L-windowLength)/step) + 1;
    E = zeros(numOfFrames,1);
    for i=1:numOfFrames
        window = (signal(curPos:curPos+windowLength-1));
        E(i) = (1/(windowLength)) * sum(abs(window.^2));
        curPos = curPos + step;
    end
end

• 谱质心

谱质心被定义为频谱的重心，设第$i$帧的谱质心为$C_i$，则：
$$C_i=\frac{{\sum }_{k=1}^N(k+1)X_i(k)}{{\sum }_{k=1}^N{X}_i(k)}$$
其中$X_i(k),k=1,\cdots ,N$是第$i$帧的离散傅里叶变换，$N$为帧长度。这个特征用来测量频谱的位置，它的值越大就表示声音越洪亮

提取谱质心序列的MATLAB程序如下：

function C = SpectralCentroid(signal,windowLength, step, fs)
%% 计算谱质心
% 输入:
% 	signal		:原始信号
% 	windowLength:帧长
% 	step		:帧移
% 输出:
% 	C			:每一帧的谱质心
    signal = signal / max(abs(signal));
    curPos = 1;
    L = length(signal);
    numOfFrames = floor((L-windowLength)/step) + 1;
    H = hamming(windowLength);
    m = ((fs/(2*windowLength))*[1:windowLength])';
    C = zeros(numOfFrames,1);
    for i=1:numOfFrames
        window = H.*(signal(curPos:curPos+windowLength-1));    
        FFT = (abs(fft(window,2*windowLength)));
        FFT = FFT(1:windowLength);  
        FFT = FFT / max(FFT);
        C(i) = sum(m.*FFT)/sum(FFT);
        if (sum(window.^2)<0.010)
            C(i) = 0.0;
        end
        curPos = curPos + step;
    end
    C = C / (fs/2);
end

调用上述函数即可得到短时能量和谱质心特征序列

[x, fs] = audioread("xxxx.wav");

% 窗长和帧移 单位：秒
win = 0.05;
step = 0.05;

% 计算短时能量
Eor = ShortTimeEnergy(x, win * fs, step * fs);
% 计算谱质心
Cor = SpectralCentroid(x, win * fs, step * fs, fs);

% 对特征序列进行中值滤波
E = medfilt1(Eor, 5);
E = medfilt1(E, 5);
C = medfilt1(Cor, 5); 
C = medfilt1(C, 5);

阈值估计和阈值化处理

接着估计两个特征序列的阈值：

1. 计算每一条特征序列的直方图

2. 对直方图进行平滑处理

3. 检测直方图的局部最大值

4. 设$M_1$和$M_2$分别为第一大和第二大的局部最大值的位置，则阈值$T$可通过以下公式算出：
   $$T=\frac{W\cdot M_1+M_2}{W+1}$$ $W$是我们自己设置的参数，显然$W$越大，阈值$T$将越靠近$M_1$

使用上述方法估计出短时能量特征和谱质心特征的阈值后，就可以进行阈值化处理

阈值估计和阈值化处理的程序如下：

% 计算特征序列的平均值
E_mean = mean(E);
Z_mean = mean(C);

Weight = 10; % 阈值估计的参数
% 寻找短时能量的阈值
Hist = histogram(E, round(length(E) / 10));  % 计算直方图
HistE = Hist.Values;
X_E = Hist.BinEdges;
[MaximaE, countMaximaE] = findMaxima(HistE, 3); % 寻找直方图的局部最大值
if (size(MaximaE, 2) >= 2) % 如果找到了两个以上局部最大值
    T_E = (Weight*X_E(MaximaE(1, 1)) + X_E(MaximaE(1, 2))) / (Weight + 1);
else
    T_E = E_mean / 2;
end

% 寻找谱质心的阈值
Hist = histogram(C, round(length(C) / 10));
HistC = Hist.Values;
X_C = Hist.BinEdges;
[MaximaC, countMaximaC] = findMaxima(HistC, 3);
if (size(MaximaC,2)>=2)
    T_C = (Weight*X_C(MaximaC(1,1))+X_C(MaximaC(1,2))) / (Weight+1);
else
    T_C = Z_mean / 2;
end

% 阈值判断
Flags1 = (E>=T_E);
Flags2 = (C>=T_C);
flags = Flags1 & Flags2;

% 画出以上过程的结果
% 短时能量
subplot(3,1,1); plot(Eor, 'g'); hold on; plot(E, 'c'); 
L = line([0 length(E)],[T_E T_E]); set(L,'Color',[0 0 0]); set(L, 'LineWidth', 2);
axis([0 length(Eor) min(Eor) max(Eor)]);
legend({'Short time energy (original)', 'Short time energy (filtered)', 'Threshold'});
% 谱质心
subplot(3,1,2); plot(Cor, 'g'); hold on; plot(C, 'c'); 
L = line([0 length(C)],[T_C T_C]); set(L,'Color',[0 0 0]); set(L, 'LineWidth', 2);   
axis([0 length(Cor) min(Cor) max(Cor)]);
legend({'Spectral Centroid (original)', 'Spectral Centroid (filtered)', 'Threshold'});    

用到的寻找局部最大值函数findMaxima为：

function [Maxima, countMaxima] = findMaxima(f, step)
%% 寻找局部最大值
%
% 输入:
% f:    输入序列
% step: 搜寻窗长
%
% 输出:
% Maxima: [2xcountMaxima] matrix containing: 
%         1. 最大值的索引
%         2. 最大值
% countMaxima: 最大值的数量

%% STEP 1: 寻找最大值
    countMaxima = 0;
    for i = 1 : length(f) - step - 1 % for each element of the sequence:
        if i > step
            if (mean(f(i - step : i - 1)) <  f(i)) && (mean(f(i + 1 : i + step))< f(i))  
                % IF the current element is larger than its neighbors (2*step window)
                % --> keep maximum:
                countMaxima = countMaxima + 1;
                Maxima(1, countMaxima) = i;
                Maxima(2, countMaxima) = f(i);
            end
        else
            if (mean(f(1 : i)) <= f(i)) && (mean(f(i + 1 : i + step)) < f(i)) 
                % IF the current element is larger than its neighbors (2*step window)
                % --> keep maximum:
                countMaxima = countMaxima + 1;
                Maxima(1, countMaxima) = i;
                Maxima(2, countMaxima) = f(i);
            end

        end
    end

    %% STEP 2: 对最大值进行进一步处理
    
    MaximaNew = [];
    countNewMaxima = 0;
    i = 0;
    while i < countMaxima
        % get current maximum:
        i = i + 1;
        curMaxima = Maxima(1,i);
        curMavVal = Maxima(2,i);

        tempMax = Maxima(1,i);
        tempVals = Maxima(2,i);

        % search for "neighbourh maxima":
        while (i < countMaxima) && ( Maxima(1,i+1) - tempMax(end) < step / 2)
            i = i + 1;
            tempMax(end + 1) = Maxima(1,i);
            tempVals(end + 1) = Maxima(2,i);
        end

        [MM, MI] = max(tempVals);

        if MM > 0.02 * mean(f) % if the current maximum is "large" enough:
            countNewMaxima = countNewMaxima + 1;   % add maxima
            % keep the maximum of all maxima in the region:
            MaximaNew(1, countNewMaxima) = tempMax(MI); 
            MaximaNew(2, countNewMaxima) = f(MaximaNew(1, countNewMaxima));
        end        
    end

    Maxima = MaximaNew;
    countMaxima = countNewMaxima;
end

运行结果如下：

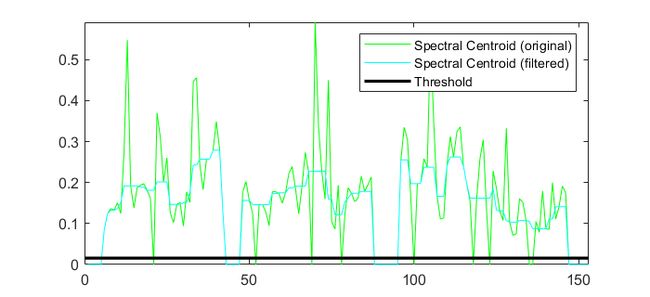
提取语音片段

经过上一步的阈值处理后，就得到了一段标记语音段的阈值化序列，接下来将该序列映射到原始信号中，从而获得语音段在原始信号中的起始和结束位置

%% 提取语音片段
count = 1;
segments = [];
while (count < length(flags)) % 当还有未处理的帧时
	% 初始化
	curX = [];	
	countTemp = 1;
	while ((flags(count) == 1) && (count < length(flags)))
		if (countTemp == 1) % 如果是该语音段的第一帧
			Limit1 = round((count-1)*step*fs)+1; % 设置该语音段的开始边界
            if Limit1 < 1
                Limit1 = 1; 
            end       
		end	
		count = count + 1; 		% 计数器加一
		countTemp = countTemp + 1;	% 当前语音段的计数器加一
	end

	if countTemp > 1 % 如果当前循环中有语音段
		Limit2 = round((count - 1) * step * fs); % 设置该语音段的结束边界
		if Limit2 > length(x)
            Limit2 = length(x);
        end
        % 将该语音段的首尾位置加入到segments的最后一行
        segments(end + 1, 1) = Limit1;
        segments(end,     2) = Limit2;
    end
	count = count + 1;
end

% 合并重叠的语音段
for i = 1 : size(segments, 1) - 1 % 对每一个语音段进行处理
    if segments(i, 2) >= segments(i + 1, 1)
        segments(i, 2) = segments(i + 1, 2);
        segments(i + 1, :) = [];
        i = 1;
    end
end

运行结果如下：

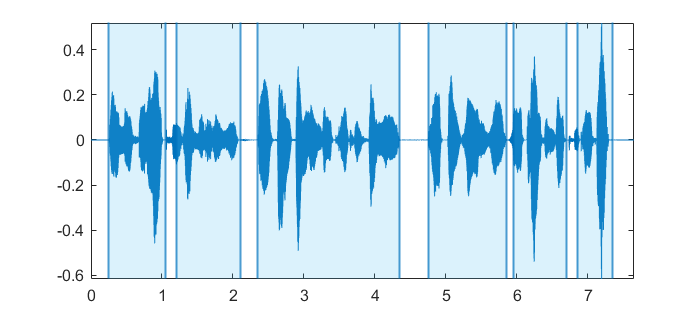
MATLAB2020a中的VAD函数

在最新的2020a中，MATLAB引入了一个端点检测函数detectSpeech，该函数也是基于上述算法的，只是将提取的两个特征由短时能量和谱质心换成了短时能量和频谱扩展度(Spectral Spread，即频谱的二阶中心距，描述信号在频谱中心周围的分布状况)

算法流程如下图所示：

步骤1~8分别为：

1. 使用短时傅里叶变换，将信号转换为时频辨识
2. 为每一帧计算短时能量和频谱扩展度
3. 分别计算上述两个特征序列的直方图
4. 阈值估计
5. 对特征序列进行平滑处理
6. 分别对平滑后的特征序列进行阈值判断
7. 将两个阈值判断结果相与，得到提取的语音片段
8. 合并重叠或者两者距离小于设定值MergeDistance的语音片段

使用该函数对一段语音进行端点检测的效果如下图所示：

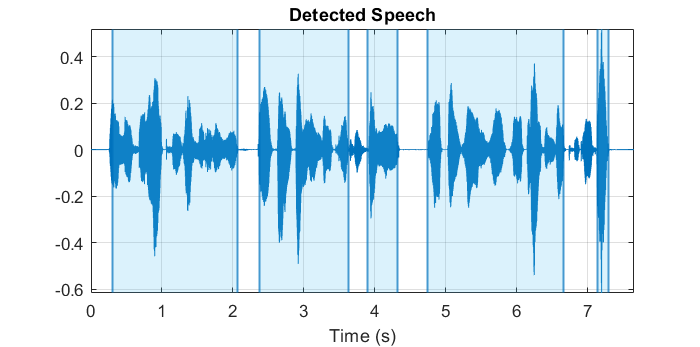
具体使用方法参见：https://www.mathworks.com/help/audio/ref/detectspeech.html

参考

Giannakopoulos, Theodoros. “A Method for Silence Removal and Segmentation of Speech Signals, Implemented in MATLAB”, (University of Athens, Athens, 2009).