【20200513】数字图像处理DIP课程课业打卡九之图像的锐化处理

叮嘟！这里是小啊呜的学习课程资料整理。好记性不如烂笔头，今天也是努力进步的一天。一起加油进阶吧！

一、DIP课程课业打卡九

一.填空题
1、对图像进行Laplacian锐化，Laplacian锐化的系数矩阵为H=[0 -1 0; -1 4 -1; 0 -1 0]。某3*3的图像块如图所示，该图像块的中心点进行Laplacian锐化后，结果为：__________ 。

正确答案：
5

解析：（-1）*2+（-1）*6+4*6+（-1）*4+（-1）*7=24-19=5

2、Laplacian算子是_____阶微分算子。

正确答案：
二

3、Wallis算子是 _____ 阶微分算子。

正确答案：
二

4、图像分割方法依照分割时所依据的图像特性不同，大致可以分为三大类：_____方法、_____分割方法、 _____ 提取方法。

正确答案：
阈值；边界；区域

5、均匀性度量法的设计思想认为，属于“同一类别”的对象具有较大的一致性。因此“同一类别”的所有像素的_____比较小。

正确答案：
方差

二、知识巩固

1、图像锐化的概念

图像锐化的 目的 是加强图像中景物的细节边缘和轮廓 。
 锐化的作用是使 灰度反差增强 。
 因为边缘和轮廓都位于灰度突变的地方。所以锐化算法的实现是基于 微分 作用。

2、图像锐化方法

 一阶微分锐化方法；
 二阶锐化微分方法 ；

3、图像细节的灰度变化特性

4、一阶微分锐化

对于一元函数f(t)，一阶微分算子可以定义如下：

 ▽ f(t)= f(t+1)- f(t)
 对于二元图像（函数）f(x,y)，一阶微分的定义是通过梯度实现的。

5、二阶微分锐化—— Laplacian 算法

从图像的景物细节的灰度分布特性可知，有些灰度变化特性一阶微分的描述不是很明确，为此，采用二阶微分能够更加获得更丰富的景物细节。

二阶微分锐化—— 景物细节对应关系

1）对于突变形的细节，通过一阶微分的极大值点，二阶微分的过0点均可以检测出来。
2）对于细线形的细节，通过一阶微分的过0点，二阶微分的极小值点均可以检测出来。
3）对于渐变的细节，一般情况下很难检测，但二阶微分的信息比一阶微分的信息略多。

由前面的推导，写成模板系数形式形式即为
Laplacian算子：

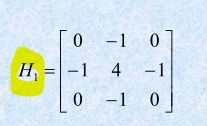
6、二阶微分锐化—— Laplacian变形算法锐化边缘提取

为了改善锐化效果，可以脱离微分的计算原理，在原有的算子基础上，对模板系数进行改变，获得Laplacian变形算子如下所示。

7、二阶微分锐化—— Wallis算法

考虑到人的视觉特性中包含一个对数环节，因此在锐化时，加入对数处理的方法来改进。

在前面的算法公式中注意以下几点：
1）为了防止对0取对数，计算时实际上是用log(f(i,j)+1);
2）因为对数值很小log(256)=5.45,所以计算时用46*log(f(i,j)+1)。
（46=255/log(256)）

算法特点：

Wallis算法考虑了人眼视觉特性，因此，与Laplacian等其他算法相比，可以对 暗区的细节进行比较好的锐化。

8、一阶与二阶微分的边缘提取效果比较

以Sobel及Laplacian算法为例进行比较。

 Sobel算子获得的边界是比较粗略的边界，反映的边界信息较少，但是所反映的边界比较清晰；
 Laplacian算子获得的边界是比较细致的边界。
反映的边界信息包括了许多的细节信息，但是所反映的边界不是太清晰。

9、关于梯度-简答题【重要】

对于一张灰度图像，其梯度是如何定义的？图像梯度的物理意义是什么？

Ending！
更多课程知识学习记录随后再来吧！

就酱，嘎啦！

注：
人生在勤，不索何获。