机器学习笔记(二)矩阵和线性代数 例:用Python实现SVD分解进行图片压缩
线性代数基本只要是理工科,都是必修的一门课。当时学习的时候总是有一个疑惑,这个东西到底是干嘛用的?为什么数学家发明出这么一套方法呢,感觉除了解方程没发现有什么大用啊!但随着学习的深入,慢慢发现矩阵的应用其实还是挺广泛的,无论是信号处理,特征提取,还是图片处理等方面都有着非常广泛的应用。
上周写了概率论的内容,发现根本没有人看啊,心好塞……所以还是不讲太多理论的内容了,就简单介绍一下线性代数中比较基本的概念,然后通过一个小应用即通过SVD分解提取图片主要特征来认识一下线性代数在机器学习中的作用。
基本概念
行列式:矩阵中任一行(或列)的各元素与其对应的代数余子式的乘积之和。
伴随矩阵:各元素代数余子式构成的矩阵的转置。
其中,伴随矩阵左乘原矩阵就可以得到一个对角元素全是行列式的对角阵。
矩阵的乘法:对应的行和列的元素相乘相加。
特别要提的是矩阵和向量的乘法,比如矩阵A(m行n列)和一个列向量(n行1列)相乘得到一个m维的列向量,那么这样其实矩阵A就对应了一个从n维空间到m维空间的线性映射(旋转,平移,侧切等)。
矩阵的秩:矩阵A中有一个不等于0的r阶子式D,并且所有的r+1阶子式全等于0,那么D称为A的最高阶非零子式,r为矩阵的秩。
这个解释其实很不友好,完全不知道它的意义在哪儿。其实所谓秩,对应的是该矩阵象空间的维数,这样就可以理解为什么可以用秩来判断方程的解的个数。对于Ax=b,如果(A,b)的秩大于A的秩,那么说明引入b后,象空间维数上升,因此原来的A的象空间无法表达b,方程无解。而如果(A,b)的秩和A相等,说明b的引入不改变A象空间的维数,因此b可在A的象空间中表示,而一旦这个秩比未知数个数还小,那么就有无穷多解了。
正交阵:若n阶矩阵满足A.T*A=I,则称A为正交矩阵。(即A的行(列)都是单位向量,且两两正交)
特征值和特征向量:若A是n阶矩阵,若 数λ和非0列向量x满足Ax=λx,则称数λ为A的特征值,x称为λ对应的特征向量。
矩阵A与其特征向量相乘得到特征值乘以该特征向量,因此矩阵对特征向量只做了拉伸变换,而这个特征值的大小表明了该特征的重要性。
特征值分解:比如对于矩阵A而言,有三个特征向量,Ax1=λ1x1,Ax2=λ2x2,Ax3=λ3x3,则有A(x1,x2,x3)=(x1,x2,x3)B,其中B为对角线是λ1,λ2,λ3的阵,再进一步就有A=(x1,x2,x3)B(x1,x2,x3)^-1。
例:利用Python进行SVD分解进行图像压缩
首先SVD分解主要是用于特征的提取。特征值分解当然也可以进行特征提取,但它要求矩阵必须是方阵,这很多时候限制了我们对它的使用。而SVD分解则对原矩阵的形状没有任何要求.
只要矩阵A非奇异,那么A.T*A必定是个对称正定阵,
所以必然存在正交矩阵Q使得Q.T(A.T*A)Q=diag(λ1,λ2,……λn),
令σi=λi^(1/2),
所以Q.T(A.T*A)Q=diag(σ1,σ2,……σn)*diag(σ1,σ2,……σn),
令P为AQdiag(σ1,σ2,……σn)^(1/2),
则有P.T*A*Q=diag(σ1,σ2,……σn),
所以A=P*diag(σ1,σ2,……σn)*Q.T。
我们利用SVD分解进行图片压缩,其实主要是保留系数矩阵中较大的值,舍掉较小的值,从而达到压缩图像的作用。
在Python中,SVD分解非常简单,可利用np.linalg.svd()函数,比如u,sigma,v=np.linalg.svd(A),则u,v分别返回A的左右奇异向量,而sigma返回的并不是系数矩阵,而是一个奇异值从大到小排列的一个向量。然后对于图像而言,其实就是RGB三个图层上矩阵的叠加,每个元素的值 为0到255之间的整数,在Python中读取图像可以通过plt.imread()函数,这样直接得到了一个a*b*3的矩阵,然后对三个图层分别处理就行。
现在来整理一下思路:
1 读取图片,分解成RGB三个矩阵。
2 对三个矩阵分别进行SVD分解,得到对应的奇异值和奇异向量。
3 按照一定标准进行奇异值的筛选(整体数量的一定百分比,或者奇异值和的一定百分比)
4 恢复矩阵,并将RGB三个矩阵叠加起来。
5 保存图像。
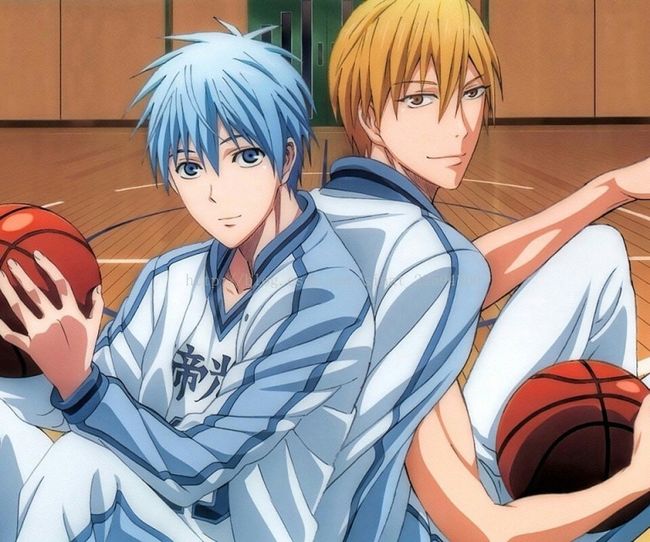
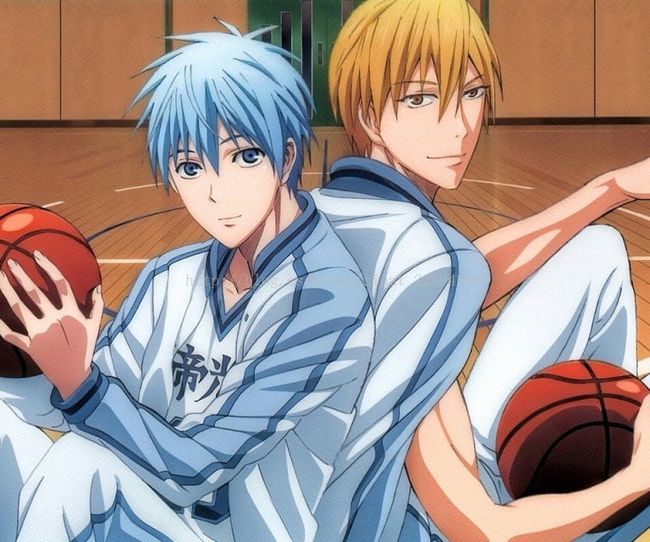
原图,黑子和黄濑
按整体数量百分比进行奇异值筛选
import numpy as np
from matplotlib import pyplot as plt
def svdimage(filename,percent):
original=plt.imread(filename)
R0=np.array(original[:,:,0])
G0=np.array(original[:,:,1])
B0=np.array(original[:,:,2])
u0,sigma0,v0=np.linalg.svd(R0)
u1,sigma1,v1=np.linalg.svd(G0)
u2,sigma2,v2=np.linalg.svd(B0)
R1=np.zeros(R0.shape)
G1=np.zeros(G0.shape)
B1=np.zeros(B0.shape)
for i in xrange(int(percent*len(sigma0))+1):
R1+=sigma0[i]*np.dot(u0[:,i].reshape(-1,1),v0[i,:].reshape(1,-1))
for i in xrange(int(percent*len(sigma1))+1):
G1+=sigma1[i]*np.dot(u1[:,i].reshape(-1,1),v1[i,:].reshape(1,-1))
for i in xrange(int(percent*len(sigma2))+1):
B1+=sigma2[i]*np.dot(u2[:,i].reshape(-1,1),v2[i,:].reshape(1,-1))
final=np.stack((R1,G1,B1),2)
final[final>255]=255
final[final<0]=0
final=np.rint(final).astype('uint8')
return final
if __name__=='__main__':
filename='test3.jpg'
for p in np.arange(.1,1,.1):
after=svdimage(filename,p)
plt.imsave(str(p)+'_0.jpg',after)
其实可以看到取前10%的奇异值图片部分信息丢失了,但到50%左右时还原度基本就很高了。
接下来我们再用奇异值总和的百分比来进行筛选。
import numpy as np
from matplotlib import pyplot as plt
def svdimage(filename,percent):
original=plt.imread(filename)
R0=np.array(original[:,:,0])
G0=np.array(original[:,:,1])
B0=np.array(original[:,:,2])
u0,sigma0,v0=np.linalg.svd(R0)
u1,sigma1,v1=np.linalg.svd(G0)
u2,sigma2,v2=np.linalg.svd(B0)
R1=np.zeros(R0.shape)
G1=np.zeros(G0.shape)
B1=np.zeros(B0.shape)
total0=sum(sigma0)
total1=sum(sigma1)
total2=sum(sigma2)
sd=0
for i,sigma in enumerate(sigma0):
R1+=sigma*np.dot(u0[:,i].reshape(-1,1),v0[i,:].reshape(1,-1))
sd+=sigma
if sd>=percent*total0:
break
sd=0
for i,sigma in enumerate(sigma1):
G1+=sigma*np.dot(u1[:,i].reshape(-1,1),v1[i,:].reshape(1,-1))
sd+=sigma
if sd>=percent*total1:
break
sd=0
for i,sigma in enumerate(sigma2):
B1+=sigma*np.dot(u2[:,i].reshape(-1,1),v2[i,:].reshape(1,-1))
sd+=sigma
if sd>=percent*total2:
break
final=np.stack((R1,G1,B1),2)
final[final>255]=255
final[final<0]=0
final=np.rint(final).astype('uint8')
return final
if __name__=='__main__':
filename='test3.jpg'
for p in np.arange(.1,1,.1):
after=svdimage(filename,p)
plt.imsave(str(p)+'_1.jpg',after)同样还是贴个0.1,0.5,0.9的图
用奇异值总和的百分比来筛选就可以明显看出特征选择的作用了,0.1的时候我大奇迹时代已经看不见了。
好啦,就到这里,希望对大家有帮助,也欢迎拍砖。