老农的计算机学习笔记(一）计算机的诞生及其基础

 菜鸟的计算机学习笔记
 ===================
 2014-06-08
 
 “万法归一”
 
 
 

改变世界的发明

 

计算工具的早期发展

计算机来源于人类对于计算工具的不断改进，但很少有人想到它能发展为人工智能，在如此之多的场合发挥作用。

最早的计算工具，例如：奇普（Quipu或khipu）是古代印加人的一种结绳记事的方法，用来计数或者记录历史。它是由许多颜色的绳结编成的。
还有古希腊人的安提凯希拉装置，中国的算盘等。中国古代最早采用的一种计算工具叫筹策，又被叫做算筹。这种算筹多用竹子制成，也有用木头，兽骨充当材料的。约二百七十枚一束，放在布袋里可随身携带。直到今天仍在使用的珠算盘，是中国古代计算工具领域中的另一项发明，明代时的珠算盘已经与现代的珠算盘几乎相同。


17世纪初，西方国家的计算工具有了较大的发展，英国数学家纳皮尔发明的"纳皮尔算筹"，英国牧师奥却德发明了计圆柱型对数算尺，这种计算尺不仅能做加减乘除、乘方、开方运算，甚至可以计算三角函数，指数函数和对数函数，这些计算工具不仅带动了计算器的发展，也为现代计算器发展奠定了良好的基础，成为现代社会应用广泛的计算工具。
1642年，年仅19岁的法国伟大科学家帕斯卡（Pascaline）发明了第一部机械式计算器，在他的计算器中有一些互相联锁的齿轮，一个转过十位的齿轮会使另一个齿轮转过一位，人们可以像拨电话号码盘那样，把数字拨进去，计算结果就会出现在另一个窗口中，但是只能做加减计算。1694年，莱布尼兹（Leibniz）在德国将其改进成可以进行乘除的计算。1819年，英国科学家巴贝奇设计“差分机”,并于1822年制造出可动模型。 这台机器能提高乘法速度和改进对数表等数字表的精确度。1991年，为纪念巴贝奇诞辰200周年，伦敦科学博物馆制作了完整差分机，它包含4000多个零件，重2.5吨。英国人查尔斯·巴贝奇研制出差分机和分析机为现代计算机设计思想的发展奠定基础。此后，一直要到20世纪50年代末才有电子计算器的出现。

电子计算机的诞生

所谓现代计算机是指采用先进的电子技术来代替陈旧落后的机械或继电器技术。现代计算机经历了半个多世纪的发展，这一时期的杰出代表人物是英国科学家图灵和美籍匈牙利科学家冯·诺依曼。图灵对现代计算机的贡献主要是：建立了图灵机的理论模型，发展了可计算性理论；提出了定义机器智能的图灵测试。冯·诺依曼的贡献主要是：确立了现代计算机的基本结构，即冯·诺依曼结构。其特点可以概括为如下几点：
（1）使用单一的处理部件来完成计算、存储以及通信的工作；
（2）存储单元是定长的线性组织；
（3）存储空间的单元是直接寻址的；
（4）使用机器语言，指令通过操作码来完成简单的操作；
（5）对计算进行集中的顺序控制。  

1946年2月14日，由美国军方定制的世界上第一台电子计算机“电子数字积分计算机”（ENIAC Electronic Numerical And Calculator）在美国宾夕法尼亚大学问世了。ENIAC（中文名：埃尼阿克）是美国奥伯丁武器试验场为了满足计算弹道需要而研制成的，这台计算器使用了17840支电子管，大小为80英尺×8英尺，重达28t（吨），功耗为170kW，其运算速度为每秒5000次的加法运算，造价约为487000美元。ENIAC的问世具有划时代的意义，表明电子计算机时代的到来。ENIAC的主要设计者是冯·诺伊曼，1945年3月他在共同讨论的基础上起草ENIAC(电子离散变量自动计算机)设计报告初稿，这对后来计算机的设计有决定性的影响，特别是确定计算机的结构，采用存储程序以及二进制编码等，至今仍为电子计算机设计者所遵循。计算机是20世纪最先进的科学技术发明之一，对人类的生产活动和社会活动产生了极其重要的影响，并以强大的生命力飞速发展。它的应用领域从最初的军事科研应用扩展到社会的各个领域，已形成了规模巨大的计算机产业，带动了全球范围的技术进步，由此引发了深刻的社会变革，计算机已遍及一般学校、企事业单位，进入寻常百姓家，成为信息社会中必不可少的工具。


ENIAC方案明确奠定了新机器由五个部分组成，包括：运算器、控制器、存储器、输入和输出设备，并描述了这五部分的职能和相互关系。报告中，诺伊曼对ENIAC中的两大设计思想作了进一步的论证，为计算机的设计树立了一座里程碑。
设计思想之一是二进制，他根据电子元件双稳工作的特点，建议在电子计算机中采用二进制。报告提到了二进制的优点，并预言，二进制的采用将大简化机器的逻辑线路。
设计思想之二是存储程序和程序控制（这也是计算机基本工作原理），把运算程序存在机器的存储器中，程序设计员只需要在存储器中寻找运算指令，机器就会自行计算，这样，就不必每个问题都重新编程，从而大大加快了运算进程。这一思想标志着自动运算的实现，已成为电子计算机设计的基本原则。
1946年7，8月间，冯·诺依曼和戈尔德斯廷、勃克斯在ENIAC方案的基础上，为普林斯顿大学高级研究所研制IAS计算机时，又提出了一个更加完善的设计报告《电子计算机逻辑设计初探》．以上两份既有理论又有具体设计的文件，首次在全世界掀起了一股“计算机热”，它们的综合设计思想，便是著名的“冯·诺依曼机”，其中心就是有存储程序原则--指令和数据一起存储（存储机）。这个概念被誉为“计算机发展史上的一个里程碑”。它标志着电子计算机时代的真正开始，指导着以后的计算机设计。自然一切事物总是在发展着的，随着科学技术的进步，今天人们又认识到“冯·诺依曼机”的不足，它妨碍着计算机速度的进一步提高，而提出了“非冯·诺依曼机”的设想。

从晶体管到集成电路

如果说冯·诺依曼奠定了计算机的体系结构，那么计算机在硬件上的成熟要归功于晶体管的发明和后来集成电路产业的飞速发展。
 
 1947年12月23日，美国新泽西州墨累山的贝尔实验室里，3位科学家——巴丁博士、布菜顿博士和肖克莱博士在紧张而又有条不紊地做着实验。他们在导体电路中正在进行用半导体晶体把声音信号放大的实验。3位科学家惊奇地发现，在他们发明的器件中通过的一部分微量电流，竟然可以控制另一部分流过的大得多的电流，因而产生了放大效应。这个器件，就是在科技史上具有划时代意义的成果——晶体管。因它是在圣诞节前夕发明的，而且对人们未来的生活发生如此巨大的影响，所以被称为“献给世界的圣诞节礼物”。另外这3位科学家因此共同荣获了1956年诺贝尔物理学奖。
 
晶体管促进并带来了“固态革命”，进而推动了全球范围内的半导体电子工业。作为主要部件，它及时、普遍地首先在通讯工具方面得到应用，并产生了巨大的经济效益。由于晶体管彻底改变了电子线路的结构，集成电路以及大规模集成电路应运而生，这样制造像高速电子计算机之类的高精密装置就变成了现实。


晶体管（transistor）是一种固体半导体器件，具有检波、整流、放大、开关、稳压、信号调制等多种功能。晶体管作为一种可变电流开关，能够基于输入电压控制输出电流。与普通机械开关（如Relay、switch）不同，晶体管利用电讯号来控制自身的开合，而且开关速度可以非常快，实验室中的切换速度可达100GHz以上。严格意义上讲，晶体管泛指一切以半导体材料为基础的单一元件，包括各种半导体材料制成的二极管、三极管、场效应管、可控硅等。晶体管有时多指晶体三极管。

基本逻辑电路

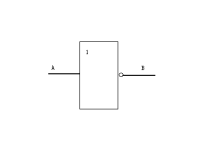
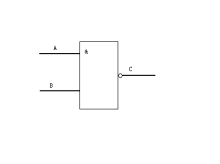
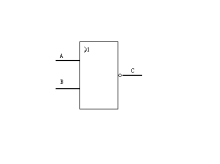
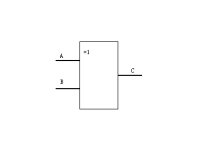
凡是对脉冲通路上的脉冲起着开关作用的电子线路就叫做门电路，是基本的逻辑电路。门电路可以有一个或多个输入端，但只有一个输出端。门电路的各输入端所加的脉冲信号只有满足一定的条件时，“门”才打开，即才有脉冲信号输出。从逻辑学上讲，输入端满足一定的条件是“原因”，有信号输出是“结果”，门电路的作用是实现某种因果关系──逻辑关系。所以门电路是一种逻辑电路。基本的逻辑关系有三种：与逻辑、或逻辑、非逻辑。与此相对应，基本的门电路有与门、或门、非门。


“门”是这样的一种电路：它规定各个输入信号之间满足某种逻辑关系时，才有信号输出，通常有下列三种门电路：与门、或门、非门（反相器）。从逻辑关系看，门电路的输入端或输出端只有两种状态，无信号以“0”表示，有信号以“1”表示。也可以这样规定：低电平为“0”，高电平为“1”，称为正逻辑。反之，如果规定高电平为“0”，低电平为“1”称为负逻辑，然而，高与低是相对的，所以在实际电路中要先说明采用什么逻辑，才有实际意义，例如，负与门对“1”来说，具有“与”的关系，但对“0”来说，却有“或”的关系，即负与门也就是正或门；同理，负或门对“1”来说，具有“或”的关系，但对“0”来说具有“与”的关系，即负或门也就是正与门。


分立元件组成：门电路可用分立元件组成，也可做成集成电路，但目前实际应用的都是集成电路。由于单一品种的与非门可以构成各种复杂的数字逻辑电路，而器件品种单一，给备件、调试都会带来很大方便，所以集成电路工业产品中并没有与门、或门，而供应与非门。

计算机发展大事记

1950年：威廉·肖克莱开发出双极晶体管（Bipolar JunctionTransistor），这是现在通行的标准的晶体管。"晶体管时代开启"。
1953年：第一个采用晶体管的商业化设备投入市场，即助听器。
1954年10月18日：第一台晶体管收音机Regency TR1投入市场，仅包含4只锗晶体管。
1961年4月25日：第一个集成电路专利被授予罗伯特·诺伊斯（Robert Noyce）。最初的晶体管对收音机和电话而言已经足够，但是新的电子设备要求规格更小的晶体管，即集成电路。“集成电路时代开始”
1965年：摩尔定律诞生。当时，戈登·摩尔（Gordon Moore）预测，未来一个芯片上的晶体管数量大约每18个月翻一倍(至今依然基本适用)，摩尔定律在Electronics Magazine杂志一篇文章中公布。
1968年7月：罗伯特·诺伊斯和戈登·摩尔从仙童（Fairchild）半导体公司辞职，创立了一个新的企业，即英特尔公司，英文名Intel为“集成电子设备（integrated electronics）”的缩写。
1969年：英特尔成功开发出第一个PMOS硅栅晶体管技术。这些晶体管继续使用传统的二氧化硅栅介质，但是引入了新的多晶硅栅电极。
1971年：英特尔发布了其第一个微处理器4004。4004规格为1/8英寸 x 1/16英寸，包含仅2000多个晶体管，采用英特尔10微米PMOS技术生产。“cpu时代”开始
1972年，英特尔发布了第一个8位处理器8008。
1978年，英特尔发布了第一款16位处理器8086。含有2.9万个晶体管。
1978年：英特尔标志性地把英特尔8088微处理器销售给IBM新的个人电脑事业部，武装了IBM新产品IBM PC的中枢大脑。16位8088处理器为8086的改进版，含有2.9万个晶体管，运行频率为5MHz、8MHz和10MHz。“pc时代”开始。
1982年：286微处理器(全称80286，意为“第二代8086”)推出，提出了指令集概念，即现在的x86指令集，可运行为英特尔前一代产品所编写的所有软件。286处理器使用了13400个晶体管，运行频率为6MHz、8MHz、10MHz和12.5MHz。
1985年：英特尔386微处理器问世，含有27.5万个晶体管，是最初4004晶体管数量的100多倍。386是32位芯片，具备多任务处理能力，即它可在同一时间运行多个程序。
1993年：英特尔·奔腾·处理器问世，含有3百万个晶体管，采用英特尔0.8微米制程技术生产。“奔腾时代”开始。
1999年2月：英特尔发布了奔腾·III处理器。奔腾III是1x1正方形硅，含有950万个晶体管，采用英特尔0.25微米制程技术生产。
2002年1月：英特尔奔腾4处理器推出，高性能桌面台式电脑由此可实现每秒钟22亿个周期运算。它采用英特尔0.13微米制程技术生产，含有5500万个晶体管。
2002年8月13日：英特尔透露了90纳米制程技术的若干技术突破，包括高性能、低功耗晶体管，应变硅，高速铜质接头和新型低-k介质材料。这是业内首次在生产中采用应变硅。
2003年3月12日：针对笔记本的英特尔·迅驰·移动技术平台诞生，包括了英特尔最新的移动处理器“英特尔奔腾M处理器”。该处理器基于全新的移动优化微体系架构，采用英特尔0.13微米制程技术生产，包含7700万个晶体管。
2005年5月26日：英特尔第一个主流双核处理器“英特尔奔腾D处理器”诞生，含有2.3亿个晶体管，采用英特尔领先的90纳米制程技术生产。
……

二进制

 冯·诺依曼建议ENIAC使用二进制，这大大便利了计算机的世界。

 二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。它的基数为2，进位规则是“逢二进一”，借位规则是“借一当二”，由18世纪德国数理哲学大师莱布尼兹发现。当前的计算机系统使用的基本上是二进制系统。
 
 优点：
（1）技术实现简单，计算机是由逻辑电路组成，逻辑电路通常只有两个状态，开关的接通与断开，这两种状态正好可以用“1”和“0”表示。
（2）简化运算规则：两个二进制数和、积运算组合各有三种，运算规则简单，有利于简化计算机内部结构，提高运算速度。
（3）适合逻辑运算：逻辑代数是逻辑运算的理论依据，二进制只有两个数码，正好与逻辑代数中的“真”和“假”相吻合。
（4）易于进行转换，二进制与十进制数易于互相转换。

（5）用二进制表示数据具有抗干扰能力强，可靠性高等优点。因为每位数据只有高低两个状态，当受到一定程度的干扰时，仍能可靠地分辨出它是高还是低。

比如，你可以用下面任何一种方式表示数字667

1 0 1 0 0 1 1 0 1 1
| − | − − | | − | |
x o x o o x x o x x
y n y n n y y n y y

 在德国图灵根著名的郭塔王宫图书馆（Schlossbiliothke zu Gotha）保存着一份弥足珍贵的手稿，其标题为：“1与0，一切数字的神奇渊源。这是造物的秘密美妙的典范，因为，一切无非都来自上帝。”这是德国天才大师莱布尼茨（Gottfried Wilhelm Leibniz，1646 - 1716）的手迹。但是，关于这个神奇美妙的数字系统，莱布尼茨只有几页异常精炼的描述。
莱布尼茨不仅发明了二进制，而且赋予了它宗教的内涵。他在写给当时在中国传教的法国耶稣士会牧师布维（Joachim Bouvet，1662 - 1732）的信中说：“第一天的伊始是1，也就是上帝。第二天的伊始是2，……到了第七天，一切都有了。所以，这最后的一天也是最完美的。因为，此时世间的一切都已经被创造出来了。因此它被写作‘7’，也就是‘111’（二进制中的111等于十进制的7），而且不包含0。只有当我们仅仅用0和1来表达这个数字时，才能理解，为什么第七天才最完美，为什么7是神圣的数字。特别值得注意的是它（第七天）的特征（写作二进制的111）与三位一体的关联。”
布维是一位汉学大师，他对中国的介绍是17、18世纪欧洲学界中国热最重要的原因之一。布维是莱布尼茨的好朋友，一直与他保持着频繁的书信往来。莱布尼茨曾将很多布维的文章翻译成德文，发表刊行。恰恰是布维向莱布尼茨介绍了《周易》和八卦的系统，并说明了《周易》在中国文化中的权威地位。
八卦是由八个符号组构成的占卜系统，而这些符号分为连续的与间断的横线两种。这两个后来被称为“阴”、“阳”的符号，在莱布尼茨眼中，就是他的二进制的中国翻版，但实际莱布尼茨是受中国阴阳太极影响，只不过他付出了诸多研究，推演出二进制。他感到这个来自古老中国文化的符号系统与他的二进制之间的关系实在太明显了，因此断言：二进制乃是具有世界普遍性的、最完美的逻辑语言。


我们可以肯定地说，这种解释与《易经》没有联系。《易经》不是数学书，而是一本“预言”，并在漫长的历史中逐渐演变为一本“智慧之书”。书里的短线意味着阴阳相对，也即天与地、光明与黑暗、造物主和大自然。六爻以不同的组合出现，人们可以借此对自然界和人类生活的变换做出各种不同的解释。比利时神父 P．Couplet（中文名字柏应理）的 Confucius．Sinarum Philosophus （《孔子，中国人的思想家，…》）第一次在欧洲发表了易经的六十四幅六爻八卦图。
这一次将数学与古代中国《易经》相联的尝试是不符合实际的。莱布尼茨的二进制数学指向的不是古代中国，而是未来。莱布尼茨在1679年3月15日记录下他的二进制体系的同时，还设计了一台可以完成数码计算的机器。我们今天的现代科技将此设想变为现实，这在莱布尼茨的时代是超乎人的想象能力的。

二进制数据的表示法

二进制数据也是采用位置计数法，其位权是以2为底的幂。例如二进制数据110.11，逢2进1，其权的大小顺序为2²、2¹、2º、2的－1次方 、2的－2次方 。对于有n位整数，m位小数的二进制数据用加权系数展开式表示，可写
二进制和十六进制，八进制一样，都以二的幂来进位的。


在现实生活和记数器中，如果表示数的“器件”只有两种状态，如电灯的“亮”与“灭”，开关的“开”与“关”。一种状态表示数码0，另一种状态表示数码1，1加1应该等于2，因为没有数码2，只能向上一个数位进一，就是采用“满二进一”的原则，这和十进制是采用“满十进一”原则完全相同。
1+1=10，10+1=11，11+1=100，100+1=101，
101+1=110，110+1=111，111+1=1000，……，
可见二进制的10表示二，100表示四，1000表示八，10000表示十六，……。
二进制同样是“位值制”。同一个数码1，在不同数位上表示的数值是不同的。如11111，从右往左数，第一位的1就是一，第二位的1表示二，第三位的1表示四，第四位的1表示八，第五位的1表示十六。


十进制1至128的二进制表示：
0=0
1=1
2=10（2的1次方）
3=11
4=100（2的2次方）
5=101
6=110
7=111
8=1000（2的3次方）
9=1001
10=1010
11=1011
12=1100
13=1101
14=1110
15=1111
16=10000（2的4次方）
17=10001
18=10010
19=10011
20=10100
21=10101
22=10110
23=10111
24=11000
25=11001
26=11010
27=11011
28=11100
29=11101
30=11110
31=11111
32=100000（2的5次方）
33=100001
34=100010
35=100011
36=100100
37=100101
38=100110
39=100111
40=101000
41=101001
42=101010
43=101011
44=101100
45=101101
46=101110
47=101111
48=110000
49=110001
50=110010
51=110011
52=110100
53=110101
54=110110
55=110111
56=111000
57=111001
58=111010
59=111011
60=111100
61=111101
62=111110
63=111111
64=1000000 （2的6次方）
65=1000001
66=1000010
67=1000011
68=1000100
69=1000101
70=1000110
71=1000111
72=1001000
73=1001001
74=1001010
75=1001011
76=1001100
77=1001101
78=1001110
79=1001111
80=1010000
81=1010001
82=1010010
83=1010011
84=1010100
85=1010101
86=1010110
87=1010111
88=1011000
89=1011001
90=1011010
91=1011011
92=1011100
93=1011101
94=1011110
95=1011111
96=1100000
97=1100001
98=1100010
99=1100011
100=1100100
101=1100101
102=1100110
103=1100111
104=1101000
105=1101001
106=1101010
107=1101011
108=1101100
109=1101101
110=1101110
111=1101111
112=1110000
113=1110001
114=1110010
115=1110011
116=1110100
117=1110101
118=1110110
119=1110111
120=1111000
121=1111001
122=1111010
123=1111011
124=1111100
125=1111101
126=1111110
127=1111111
128=10000000 （2的7次方）
……
256=100000000（2的8次方）
……
512=1000000000（2的9次方）

……

1024=10000000000（2的10次方）

从中也可以看出，二进制的一个缺点就是太长（以位数换简单），中国人口13亿，用二进制表示就是1001101011111000110110100000000。




那么，如何表示分数和小数呢？

在十进制中，分数可以统一用小数（有限和无限，循环和不循环小数）来表示。0.1就是10的－1次方，0.01就是10的－2次方。对于二进制，一样可以，只不过精度单位分别是2的－1次方（1/2），2的－2次方（1/4），2的－3次方（1/8），……所以二进制的精度单位（在十进制看来）太“稀疏”，很多十进制小数是不能用有限的二进制小数来表示的。

1/3 = 0 × 2⁻¹ + 1 × 2⁻² + 0 × 2⁻³ + 1 × 2⁻⁴ + ... = 0.3125 + ... 

分数	十进制	二进制	分数合成
1/1	1	1
1/2	0.5	0.1	1/2
1/3	0.333...	0.010101...	1/4 + 1/16 + 1/64 . . .
1/4	0.25	0.01	1/4
1/5	0.2	0.00110011...	1/8 + 1/16 + 1/128 . . .
1/6	0.1666...	0.0010101...	1/8 + 1/32 + 1/128 . . .
1/7	0.142857142857...	0.001001...	1/8 + 1/64 + 1/512 . . .
1/8	0.125	0.001	1/8
1/9	0.111...	0.000111000111...	1/16 + 1/32 + 1/64 . . .
1/10	0.1	0.000110011...	1/16 + 1/32 + 1/256 . . .
1/11	0.090909...	0.00010111010001011101...	1/16 + 1/64 + 1/128 . . .
1/12	0.08333...	0.00010101...	1/16 + 1/64 + 1/256 . . .
1/13	0.076923076923...	0.000100111011000100111011...	1/16 + 1/128 + 1/256 . . .
1/14	0.0714285714285...	0.0001001001...	1/16 + 1/128 + 1/1024 . . .
1/15	0.0666...	0.00010001...	1/16 + 1/256 . . .
1/16	0.0625 or 0.0624999...	0.0001	1/16

计算机中的十进制小数用二进制通常是用乘二取整法来获得的。

比如0.65换算成二进制就是：

0.65 × 2 = 1.3 取1，留下0.3继续乘二取整

0.3 × 2 = 0.6 取0， 留下0.6继续乘二取整

0.6 × 2 = 1.2 取1，留下0.2继续乘二取整

0.2 × 2 = 0.4 取0， 留下0.4继续乘二取整

0.4 × 2 = 0.8 取0， 留下0.8继续乘二取整

0.8 × 2 = 1.6 取1， 留下0.6继续乘二取整

0.6 × 2 = 1.2 取1，留下0.2继续乘二取整

.......

一直循环，直到达到精度限制才停止（所以，计算机保存的小数一般会有误差，所以在编程中，要想比较两个小数是否相等，只能比较某个精度范围内是否相等。）。这时，十进制的0.65，用二进制就可以表示为：0.1010011。

还值得一提的是，在计算机中，除了十进制是有符号的外，其他如二进制、八进制、16进制都是无符号的。

二进制的运算

二进制的运算和十进制十分相似，最常用的是加法运算和乘法运算。

     加法

有四种情况： 0+0=0

0+1=1

1+0=1

1+1=10

0 进位为1

【例1103】求 1011（11）+11（3） 的和

乘法

有四种情况： 0×0=0

1×0=0

0×1=0

1×1=1

例：1001010（74） ×1010110（86）=1100011011100（6364）。其实，二进制的乘法最简单，因为用竖式表示就是“逢0全0，逢1照抄”。

减法

有四种情况：0－0=0，1－0=1，1－1=0，0－1=1。

       同样需要借位。

除法

是乘法的逆运算，用试乘和减法算商和余数。

拈加法

拈加法二进制是加减乘除外的一种特殊算法。

拈加法运算与进行加法类似，但不需要做进位。此算法在 博弈论（Game Theory）中被广泛利用。

逻辑运算与位运算

与布尔代数结合后，二进制数可进行多种逻辑运算和位运算，详见后文。

十六进制

这里捎带提一下十六进制，因为这也是一种在计算机中常用的进制，可以看成二进制的一种衍生。

二进制虽然很简单，但是太长了，比如100就要写成1100110，而底数越大，表示就越短。十六进制就有这个优点，而且和二进制可以方便地转换。

十六进制， 英文名称：hexadecimal number system，是计算机中数据的一种表示方法。同我们日常中的 十进制 表示法不一样。它由0-9,A-F组成，字母不区分大小写，逢16进位。与10进制的对应关系是：0-9对应0-9;A-F对应10-15;N进制的数可以用0---(N-1)的数表示超过9的用字母A-Z。

环境	格式	备注
URL	%hex
XML,XHTML	&#xhex
HTML,CSS	#hex	6位,用于表示颜色
Unicode	U+hex	6位,表示字符编码
MIME	=hex
Modula-2	#hex
Smalltalk,ALGOL 68	16rhex
Common Lisp	#xhex或#16rhex
IPv6	8个hex用:分隔

16进制就是逢16进1，但我们只有0~9这十个数字，所以我们用A，B，C，D，E，F这六个字母来分别表示10，11，12，13，14，15。字母不区分大小写。

十六进制数的第0位的权值为16的0次方，第1位的权值为16的1次方，第2位的权值为16的2次方……

所以，在第N（N从0开始）位上，如果是是数 X （X 大于等于0，并且X小于等于 15，即：F）表示的大小为 X×16的N次方。

假设有一个十六进数 2AF5

直接计算就是：

5×16 0+F×16 1+A×16 2+2×16 3=10997

也可以用竖式表示：

第0位： 5×16 0=5

第1位： F×16^1=240

第2位： A×16 2=2560

第3位： 2×16 3=8192

-------------------------------

10997

十六进制主要应用在

环境	格式	备注
URL	%hex	表示网址
XML,XHTML	&#xhex
HTML,CSS	#hex	6位,用于表示颜色
Unicode	U+hex	6位,表示字符编码
MIME	=hex
Modula-2	#hex
Smalltalk,ALGOL 68	16rhex
Common Lisp	#xhex或#16rhex
IPv6	8个hex用:分隔	表示ip地址

另外，在逻辑电路和计算机内存中也广泛使用十六进制表示。 

在C／Java等现代程序语言中，用0x前缀区分16进制数。

1-64 的进制对照表

10进制	2进制	16进制
1	1	1
2	10	2
3	11	3
4	100	4
5	101	5
6	110	6
7	111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F
16	10000	10
17	10001	11
18	10010	12
19	10011	13
20	10100	14
21	10101	15
22	10110	16
23	10111	17
24	11000	18
25	11001	19
26	11010	1A
27	11011	1B
28	11100	1C
29	11101	1D
30	11110	1E
31	11111	1F
32	100000	20
33	100001	21
34	100010	22
35	100011	23
36	100100	24
37	100101	25
38	100110	26
39	100111	27
40	101000	28
41	101001	29
42	101010	2A
43	101011	2B
44	101100	2C
45	101101	2D
46	101110	2E
47	101111	2F
48	110000	30
49	110001	31
50	110010	32
51	110011	33
52	110100	34
53	110101	35
54	110110	36
55	110111	37
56	111000	38
57	111001	39
58	111010	3A
59	111011	3B
60	111100	3C
61	111101	3D
62	111110	3E
63	111111	3F
64	1000000	40

转换

二进制数转换成十六进制数：二进制数转换成十六进制数时，只要从小数点位置开始，向左或向右每四位二进制划分一组（不足四位数可补0），然后写出每一组二进制数所对应的十六进制数码即可。

十六进制数转换成二进制数：把每一个十六进制数转换成4位的二进制数，就得到一个二进制数。

十六进制数字与二进制数字的对应关系如下：

0000 -> 0      0100 -> 4      1000 -> 8      1100 -> C

0001 -> 1      0101 -> 5      1001 -> 9      1101 -> D

0010 -> 2      0110 -> 6      1010 -> A       1110 -> E

0011 -> 3       0111 -> 7      1011 -> B       1111 -> F

【例】：将十六进制数5DF.9 转换成二进制：

5 D F ． 9

0101 1101 1111 ．1001

即：（5DF.9）16 =（10111011111.1001）2

【例】：将二进制数1100001.111 转换成十六进制：

0110 0001 ． 1110

6 1 ． E

即：（1100001.111）2 =（61.E）16

原码、反码和补码

如何在计算机中表示正负数呢？在计算机中，正数使用原码表示，负数使用补码表示。使用补码不但解决了0的二重表示的问题，而且可以（1）把减法变加法；（2）让符号位统一参与运算，这样大大简化了计算机的设计。

一. 机器数和真值

在学习原码, 反码和补码之前, 需要先了解机器数和真值的概念.

1、机器数

一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号, 正数为0, 负数为1.

比如，十进制中的数 +3 ，计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011 。

那么，这里的 00000011 和 10000011 就是机器数。

2、真值

因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 10000011，其最高位1代表负，其真正数值是 -3 而不是形式值131（10000011转换成十进制等于131）。所以，为区别起见，将带符号位的机器数对应的真正数值称为机器数的真值。

例：0000 0001的真值 = +000 0001 = +1，1000 0001的真值 = –000 0001 = –1


二、 原码, 反码, 补码的基础概念和计算方法.

在探求为何机器要使用补码之前, 让我们先了解原码, 反码和补码的概念.对于一个数, 计算机要使用一定的编码方式进行存储. 原码, 反码, 补码是机器存储一个具体数字的编码方式.

1. 原码

原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:

[+1]原 = 0000 0001

[-1]原 = 1000 0001

第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:

[1111 1111 , 0111 1111]

即

[-127 , 127]

原码是人脑最容易理解和计算的表示方式.

2. 反码

反码的表示方法是:

正数的反码是其本身

负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.

[+1] = [00000001]原 = [00000001]反

[-1] = [10000001]原 = [11111110]反

可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.

3. 补码

补码的表示方法是:

正数的补码就是其本身

负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

[+1] = [00000001]原 = [00000001]反 = [00000001]补

[-1] = [10000001]原 = [11111110]反 = [11111111]补

对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.



三. 为何要使用原码, 反码和补码

在开始深入学习前, 我的学习建议是先"死记硬背"上面的原码, 反码和补码的表示方式以及计算方法.

现在我们知道了计算机可以有三种编码方式表示一个数. 对于正数因为三种编码方式的结果都相同:

[+1] = [00000001]原 = [00000001]反 = [00000001]补

所以不需要过多解释. 但是对于负数:

[-1] = [10000001]原 = [11111110]反 = [11111111]补

可见原码, 反码和补码是完全不同的. 既然原码才是被人脑直接识别并用于计算表示方式, 为何还会有反码和补码呢?

首先, 因为人脑可以知道第一位是符号位, 在计算的时候我们会根据符号位, 选择对真值区域的加减. (真值的概念在本文最开头). 但是对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单. 计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法. 我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了.

于是人们开始探索 将符号位参与运算, 并且只保留加法的方法. 首先来看原码:

计算十进制的表达式: 1-1=0

1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2

如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数.

为了解决原码做减法的问题, 出现了反码:

计算十进制的表达式: 1-1=0

1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0

发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[0000 0000]原和[1000 0000]原两个编码表示0.

于是补码的出现, 解决了0的符号以及两个编码的问题:

1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原

这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:

(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补

-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)

使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].

因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-231, 231-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.

浮点数

解决了正负数表示的问题，再来看看表示实数（主要是无限小数）的问题。没想到，这还是一个异常复杂的问题。

由于二进制无法在有限的位中精确表达一些小数，所以需要一种在一定精度范围内表达实数（带小数点的数）的统一方法。科学家们发现使用类似科学计数法的方法可以，比如152853.5047表示为1.528535047×10^5。 这种结构中，s被称为尾数，10是基数，e是指数。尾数决定了精度。二进制就是使用2为基数的科学计数法，一般尾数写为1.xxxx的形式。比如π写成1.5707964 x 2 ¹， 二进制形式就是11001001 00001111 11011011（小数点在第一位后）。

To calculate π the formula is

where n is the normalized significand's n-th

由于小数点的位置可能是不固定的，所以叫做“浮点数(floating point number)”。由于各计算机厂家对实数的表示法规格不统一，带来了很大混乱，所以80年代初，通过了IEEE-754（IEC60559）标准来规范了浮点数的实现。

该标准规定基数为2，阶码E用移码（原码加上偏置值） 表示，尾数M用原码表示，根据二进制的规格化方法，数值的最高位总是1，该标准将这个1省略（缺省存储），使得尾数表示范围比实际存储的多一位。IEEE754标准中规定了5种基本浮点数格式和三种扩展模式，基本模式中最常用的有三种， 它们的具体格式如下表：

单精度（single） 总位数32位（4字节），符号位1位，指数8位（－126～127），偏置值＋127，尾数23位（约7位10进制小数）。

双精度（double） 总位数64位（8字节），符号位1位，指数11位（－1022～1023），偏置值＋1023，尾数52位（约16位10进制小数）。

扩展双精度（long double） 总位数80位（10字节），符号位1位，指数15位（－16382～16383），偏置值＋16383，尾数64位（约19位10进制小数），

单精度下的π 表示为01000000 01001001 00001111 11011011

首位的0代表符号位（＋）。其后8位10000000代表指数128（1加偏置值127），最后23位是尾数1001001 00001111 11011011（转换成十进制就是0.5707964，前面的1省略）。

0        10000000     10010010000111111011011

符号   指数（8位） 尾数（23位）

指数部分之所以使用移码是因为指数有正有负，为便于存储（不能再来一个符号位）和运算，指数统一为正数。都加上一个偏置值，使负的变为正的。比如单精度浮点，都加上127，使得指数为－126～－1的变成了指数1～126的，而指数1～127的变成了指数127～254的小数。因为偏置值为127，所以单精度浮点小数的取值范围只能在2的－126次方到2的127次方之间（不能超出偏置值，否则加完后还是会出现负数）。至于偏置值为什么选127，首先这是2的n次方减一，加它等于在1后面添多个0（移位），而127恰好是2的8次方的一半减一，考虑到正负，适合8位指数位所能表示的最大范围。

双精度下的38414.4转换成二进制：

38414的二进制是1001011000001110，而0.4=0.5*0+0.25*1+0.125*1+0.0625*0+……＝0110011001100110......（无限循环的0110）。

38414.4=1001011000001110.0110011001100110......用科学计数法表示为1.00101100000111001100110......x2¹⁵ 

指数15加上偏置值1023是1038，二进制是10000001110，因此38414.4的二进制表示是：

0            10000001110      001011000001110 0110 0110 0110 0110 0110 0110 0110 0110 0110 0

符号位   指数（11位）      尾数（52位）

对于阶码E为0或255的情况，IEEE754标准有特别的规定：

如果  E 是0 并且  M 是0，则这个数的真值为±0（正负号和数符位有关） 如果  E = 255 并且  M 是0，则这个数的真值为±∞（同样和符号位有关） 如果  E = 255 并且  M 不是0，则这不是一个数（NaN）。

浮点加法减法运算

设有两个浮点数x和y,它们分别为
x = Mx*2^Ex
y = My*2^Ey
其中Ex和Ey分别为数x和y的阶码,Mx和My为数x和y的尾数。
两浮点数进行加法和减法的运算规则是
设 Ex小于等于Ey，则 x±y = (Mx*2^(Ex－Ey)±My)*2^Ey,
完成浮点加减运算的操作过程大体分为四步：
1. 0 操作数的检查；
2. 比较阶码大小并完成对阶；
3. 尾数进行加或减运算；
4. 结果规格化并进行舍入处理。
⑴ 0 操作数检查
浮点加减运算过程比定点运算过程复杂。如果判知两个操作数x或y中有一个数为0,即可得知运算结果而没有必要再进行后续的一系列操作以节省运算时间。0操作数检查步骤则用来完成这一功能。
⑵ 比较阶码大小并完成对阶
两浮点数进行加减，首先要看两数的阶码是否相同，即小数点位置是否对齐。若二数阶码相同，表示小数点是对齐的，就可以进行尾数的加减运算。反之，若二数阶码不同，表示小数点位置没有对齐，此时必须使二数阶码相同，这个过程叫作对阶。
要对阶，首先应求出两数阶码Ex和Ey之差，即
△E = Ex－Ey
若△E=0,表示两数阶码相等，即Ex=Ey；若△E>0,表示Ex>Ey；若△E<0,表示Ex 当Ex≠Ey 时，要通过尾数的移动以改变Ex或Ey,使之相等。原则上，既可以通过Mx移位以改变Ex来达到Ex=Ey,也可以通过My移位以改变Ey来实现Ex=Ey。但是，由于浮点表示的数多是规格化的，尾数左移会引起最高有效位的丢失，造成很大误差。尾数右移虽引起最低有效位的丢失，但造成误差较小。因此，对阶操作规定使尾数右移，尾数右移后阶码作相应增加，其数值保持不变。显然，一个增加后的阶码与另一个阶码相等，增加的阶码的一定是小阶。因此在对阶时，总是使小阶向大阶看齐，即小阶的尾数向右移位(相当于小数点左移）每右移一位，其阶码加1,直到两数的阶码相等为止，右移的位数等于阶差△E。

例如123456.7+101.7654:

  e=5;  s=1.234567     (123456.7)
   + e=2;  s=1.017654     (101.7654)

  e=5;  s=1.234567
   + e=5;  s=0.001017654  (after shifting)
--------------------
     e=5;  s=1.235584654  (true sum: 123558.4654)

⑶ 尾数求和运算

对阶结束后，即可进行尾数的求和运算。不论加法运算还是减法运算，都按加法进行操作，其方法与定点加减法运算完全一样。
⑷ 结果规格化
在浮点加减运算时，尾数求和的结果也可以得到01.ф…ф或10.ф…ф，即两符号位不等，这在定点加减法运算中称为溢出，是不允许的。但在浮点运算中，它表明尾数求和结果的绝对值大于1,向左破坏了规格化。此时将运算结果右移以实现规格化表示，称为向右规格化。规则是：尾数右移1位，阶码加1。当尾数不是1.M时需向左规格化。
⑸ 舍入处理
在对阶或向右规格化时，尾数要向右移位，这样，被右移的尾数的低位部分会被丢掉，从而造成一定误差，因此要进行舍入处理。
简单的舍入方法有两种：一种是"0舍1入"法，即如果右移时被丢掉数位的最高位为0则舍去，为1则将尾数的末位加"1"。另一种是"恒置一"法，即只要数位被移掉，就在尾数的末尾恒置"1"。
在IEEE754标准中，舍入处理提供了四种可选方法：
就近舍入其实质就是通常所说的"四舍五入"。例如，尾数超出规定的23位的多余位数字是10010,多余位的值超过规定的最低有效位值的一半，故最低有效位应增1。若多余的5位　是01111,则简单的截尾即可。对多余的5位10000这种特殊情况：若最低有效位现为0,则截　尾；若最低有效位现为1,则向上进一位使其变为 0。
朝0舍入 即朝数轴原点方向舍入，就是简单的截尾。无论尾数是正数还是负数，截尾都使取值的绝对值比原值的绝对值小。这种方法容易导致误差积累。
朝+∞舍入 对正数来说，只要多余位不全为0则向最低有效位进1；对负数来说则是简单的截尾。
朝－∞舍入 处理方法正好与 朝+∞舍入情况相反。对正数来说,只要多余位不全为0则简单截尾；对负数来说，向最低有效位进1。
⑹ 溢出处理
浮点数的溢出是以其阶码溢出表现出来的。在加\减运算过程中要检查是否产生了溢出：若阶码正常，加（减）运算正常结束；若阶码溢出，则要进行相应处理。另外对尾数的溢出也需要处理。
阶码上溢 超过了阶码可能表示的最大值的正指数值，一般将其认为是+∞和－∞。
阶码下溢 超过了阶码可能表示的最小值的负指数值，一般将其认为是0。
尾数上溢 两个同符号尾数相加产生了最高位向上的进位，将尾数右移，阶码增1来重新对齐。
尾数下溢 在将尾数右移时，尾数的最低有效位从尾数域右端流出，要进行舍入处理。

    浮点数的乘除运算

乘法就是指数相加，尾数相乘；除法就是指数相减，尾数相除。

例如4734.612 x 541724.2

  e=3;  s=4.734612
    × e=5;  s=5.417242
-----------------------
     e=8;  s=25.648538980104 (true product)
     e=8;  s=25.64854        (after rounding)
     e=9;  s=2.564854        (after normalization)

布尔代数和逻辑电路

布尔代数，将逻辑和数学完美统一，奠定了人工智能的基石。

布尔代数的由来

布尔（Geroge Boole）是19世纪英国的一位中学数学老师，还创办过一所中学。后来在爱尔兰科克的一所学院当教授。生前没人认为他是数学家，虽然他曾经在剑桥大学的数学杂志上发表过论文。布尔在工作之余，喜欢阅读数学论著，思考数学问题。1854年，布尔的《思维规律》（An Investigation of the Law of Thoughts, on which are founded the Mathematical Theories of Logic and Probabilities)一书，第一次向人们展示了如何用数学的方法解决逻辑问题。在此之前，人们普遍的认识是数学和逻辑是两个不同的学科。

布尔代数将逻辑简化为两个元素：真（true)和假（false），和三种运算：与（AND）、或（OR）、非（NOT)，全部的运算只用下列几张真值表就能完全描述清楚。

与运算                

AND    1      0     

---------------------

   1      1       0

   0      0       0

如果AND运算的两个元素有一个是0，则运算结果总是0.如果两个元素都是1，运算结果才是1。例如，“太阳从西边升起”这个判断是假的（0），“水可以流动”这个判断是真的（1），那么，“太阳从西边升起并且水可以流动”就是假的（0）。

或运算

OR      1       0

----------------------

1          1       1 

0          1       0

如果OR运算的两个元素有一个是真的，则运算结果就是真（1）。如果两个元素都是0，则运算结果是0。比如，“张三是比赛第一名”这个结论是假的（0），“李四是比赛第一名”是真的（1），那么“张三或者李四是比赛第一名”就是真的（1）。

非运算（取反运算）

NOT    

-------------------

1          0

0          1

NOT运算把1变成0， 把0变成1。比如，如果“象牙是白的”是真的（1），那么“象牙不是白的”（NOT“象牙是白的”）就是假的（0）。

这么简单的理论能解决什么问题？和布尔同时代的数学家也有同样的疑问。事实上，在布尔代数提出后的80多年里，它确实没有什么像样的应用，直到1938年香农在他的硕士论文中用布尔代数实现了开关电路，才使得布尔代数成为数字电路的基础。所有的数学和逻辑运算，包括加、减、乘、除、乘方、开方等全都能转换成二值的布尔运算。

逻辑电路

1938年香农在MIT获得电气工程硕士学位，硕士论文题目是《A Symbolic Analysis of Relay and Switching Circuits》（继电器与开关电路的符号分析）。当时他已经注意到电话交换电路与 布尔代数 之间的类似性，即把布尔代数的“真”与“假”和电路系统的“开”与“关”对应起来，并用1和0表示。于是他用布尔代数分析并优化开关电路，这就奠定了数字电路的理论基础。 哈佛大学 的Howard Gardner教授说，“这可能是本世纪最重要、最著名的一篇硕士论文。”

逻辑电路（logic gates)是一种以二进制为原理、实现数字信号逻辑运算和操作的电路。分组合逻辑电路和时序逻辑电路。前者由最基本的“与门”电路、“或门电路”和“非门”电路组成，其输出值仅依赖于其输入变量的当前值，与输入变量的过去值无关—即不具记忆和存储功能；后者也由上述基本逻辑门电路组成，但存在反馈回路—它的输出值不仅依赖于输入变量的当前值，也依赖于输入变量的过去值。由于只分高、低电平，抗干扰力强，精度和保密性佳。广泛应用于计算机、数字控制、通信、自动化和仪表等方面。最基本的有与电路、或电路和非电路。

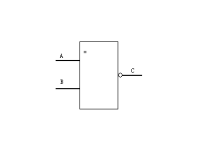
主要包括内容有数字电子技术（几种逻辑电路）、门电路基础（半导体特性，分立元件、TTL集成电路CMOS集成门电路）、组合逻辑电路（加法器、编码器、译码器等集成逻辑功能）时序逻辑电路（计数器、寄存器）以及数模和模数转换。简单的逻辑电路通常是由门电路构成，也可以用三极管来制作，例如，一个NPN三极管的集电极和另一个NPN三极管的发射极连接，这就可以看作是一个简单的与门电路，即：当两个三极管的基极都接高电平的时候，电路导通，而只要有一个不接高电平，电路就不导通……

非门：利用内部结构，使输入的电平变成相反的电平，高电平（1）变低电平（0），低电平（0）变高电

平（1）。

A	B
0	1
1	0

与门：利用内部结构，使输入两个高电平（1），输出高电平（1），不满足有两个高电平（1）则输出低电平（0）。

A	B	C
0	0	0
0	1	0
1	0	0
1	1	1

或门：利用内部结构，使输入至少一个输入高电平（1），输出高电平（1），不满足有两个低电（0）输出高电平（1）

A	B	C
0	0	0
0	1	1
1	0	1
1	1	1

与非门：利用内部结构，使输入至多一个输入高电平（1），输出高电平（1），不满足有两个高电平（1）输出高电平（1）。

A	B	C
0	0	1
0	1	1
1	0	1
1	1	0

或非门：利用内部结构，使输入两个输入低电平（0），输出高电平（1），不满足有至少一个高电平（1）输出高电平（1）。

A	B	C
0	0	1
0	1	0
1	0	0
1	1	0

异或门：当输入端同时处于低电平（0）或高电平（1）时，输出端输出低电平（0），当输入端一个为高电平（1），另一个为低电平时（0），输出端输出高电平（1）。

A	B	C
0	0	0
0	1	1
1	0	1
1	1	0

同或门：当输入端同时输入低电平（0）或高电平（1）时，输出端输出高电平（1），当输入端一个为高电平（1），另一个为低电平时（0），输出端输出低电平（0）。

A	B	C
0	0	1
0	1	0
1	0	0
1	1	1

常用组合逻辑电路有加法器、编码器、译码器及数据分配器、数据选择器、图案移位器、数码比较器、 奇偶校验码的产生器/校验器等。

时序逻辑电路包括 锁存器、寄存器、移位寄存器、计数器、触发器等。其中触发器又是构成存储器（包括各种RAM和ROM)的基础。

现在，常用的逻辑电路都已用集成电路实现，而且集成度越来越高，还出现了各种现场可编程的逻辑电路（PLD/FPGA)。

数字集成电路 按导电类型可分为 双极型集成电路 （主要为TTL）和单极型集成电路（ CMOS 、NMOS、PMOS等）。

TTL全称Transistor-Transistor Logic,即BJT-BJT 逻辑门电路，是 数字电子技术中常用的一种逻辑门电路，应用较早，技术已比较成熟。TTL主要有BJT（Bipolar Junction Transistor 即双极结型晶体管， 晶体三极管）和电阻构成，具有速度快的特点。最早的TTL门电路是74系列，后来出现了74H系列，74L系列，74LS,74AS,74ALS等系列。但是由于TTL功耗大等缺点，正逐渐被 CMOS 电路取代。

TTL电平 信号被利用的最多是因为通常数据表示采用二进制规定，+5V等价于逻辑“1”，0V等价于逻辑“0”，这被称做TTL（晶体管-晶体管 逻辑电平 ）信号系统，这是 计算机处理器 控制的设备内部各部分之间通信的标准技术。

TTL 电平信号对于 计算机处理器控制的设备内部的数据传输是很理想的，首先计算机处理器控制的设备内部的数据传输对于电源的要求不高以及热损耗也较低，另外TTL电平信号直接与 集成电路连接而不需要价格昂贵的线路 驱动器以及接收器电路；再者，计算机处理器控制的设备内部的数据传输是在高速下进行的，而TTL接口的操作恰能满足这个要求。TTL型通信大多数情况下，是采用并行数据传输方式，而并行数据传输对于超过10英尺的距离就不适合了。这是由于可靠性和成本两面的原因。因为在并行接口中存在着偏相和不对称的问题，这些问题对可靠性均有影响。

TTL输出高电平>2.4V，输出低电平<0.4V。在室温下，一般输出高电平是3.5V，输出低电平是0.2V。最小输入高电平和最大输入低电平：输入高电平>=2.0V，输入低电平<=0.8V， 噪声容限是0.4V。

TTL电路是电流控制器件，TTL电路的速度快，传输延迟时间短(5-10 纳秒)，但是功耗大。

       

CMOS，全称Complementary Metal Oxide Semiconductor，即互补金属氧化物半导体，是一种大规模应用于集成电路芯片制造的原料。采用CMOS技术可以将成对的金属氧化物半导体 场效应晶体管（MOSFET）集成在一块硅片上。该技术通常用于生产 RAM和交换应用系统。

CMOS由PMOS管和NMOS管共同构成，它的特点是低功耗。由于CMOS中一对MOS组成的门电路在瞬间要么PMOS导通、要么NMOS导通、要么都截至，比线性的三极管（BJT）效率要高得多，因此功耗很低。

相对于其他逻辑系列， CMOS逻辑电路具有以下优点：

⒈CMOS是场效应管构成，TTL为 双极晶体管构成

⒉CMOS的 逻辑电平范围比较大（5～15V），TTL只能在5V下工作

⒊CMOS的高低电平之间相差比较大、抗干扰性强，TTL则相差小，抗干扰能力差

⒋CMOS功耗很小，TTL功耗较大（1～5mA/门）

⒌CMOS的工作频率较TTL略低，但是高速CMOS速度与TTL差不多相当。

模拟电路和数字电路

模拟电路

一切计算机硬件的基础是模拟电路和数字电路。

模拟电路（Analog Circuit）：处理模拟信号的电子电路 模拟信号：时间和幅度都连续的信号（连续的含义是在某以取值范围那可以取无穷多个数值）。是涉及连续函数形式模拟信号的电子电路，与之相对的是数字电路，后者通常只关注0和1两个逻辑电平。“模拟”二字主要指电压（或电流）对于真实信号成比例的再现，它最初来源于希腊语词汇ανάλογος，意思是“成比例的。

模拟电路的 特点有：

1、函数的取值为无限多个；
2、当图像信息和声音信息改变时，信号的波也改变，即模拟信号待传播的信息包含在它的波形之中（信息变化规律直接反映在模拟信号的幅度、频率和相位的变化上）。
3.初级模拟电路主要解决两个大的方面：1放大、2信号源。
4、模拟信号具有连续性。

模拟电子技术主要类别
一.半导体器件
包括半导体特性，半导体二极管，双极结性三极管，场效应三极管等
导电性介于良导电体与绝缘体之间，利用半导体材料特殊电特性来完成特定功能的电子器件。
二.放大电路的基本原理和分析方法：1.原理：单管共发射极放大电路；双极性三极管的三组态---共射 共基 共集；场效应管放大电路－－共源极放大。分压自偏压式共 源极放大，共漏极放大，多级放大，2方法 直流通路与交流通路；静态工作点的分析；微变等效电路法；图解法等等。
三.放大电路的频率响应
单管共射放大电路的频响－－下限频率，上限频率和通频带频率失真波特图多级放大电路的频响
四.功率放大
互补对称功率放大电路—— OTL（省去输出变压器），OCL（实用电路）
五.集成放大电路
放大电路（amplification circuit）能够将一个微弱的交流小信号（叠加在直流工作点上），通过一个装置（核心为三极管、场效应管），得到一个波形相似（不失真），但幅值却大很多的交流大信号的输出。实际的放大电路通常是由信号源、晶体三极管构成的放大器及负载组成。
偏置电路，差分放大电路，中间级，输出级。
六.放大电路的反馈
正反馈和负反馈
负反馈：四组态——电压串联，电压并联，电流串联，电流并联负反馈。（注意输出电阻和输入电阻的改变）
负反馈的分析：Af=1/F（深度负反馈时）
七.模拟信号运算电路
理想运放的特点（虚短虚地）；
比例运放（反向比例运放,同向比例运放，差分比例运放）；
求和电路（反向输入求和，同向输入求和）
积分电路，微分电路；
对数电路，指数电路；
乘法电路，除法电路。
八.信号处理电路
有源滤波器（ 低通LPF，高通HPF。带通BPF，带阻BEF）
电压比较器（过零比较器，单限比较器,滞回比较器，双限比较器）
九.波形发生电路
正弦波振荡电路（条件，组成，分析步骤）
RC正弦波振荡电路（RC串并联网络选频特性）
LC 正弦波振荡电路 （LC并联网络选频特性电感三点式电容三点式）
石英晶体振荡器
非正弦波振荡器（矩形波，三角波，锯齿形发生器）

十.直流电路
单相整流电路
滤波电路（电容滤波，电感滤波 ,复式滤波）
倍压整流电路（二倍压整流电路，多倍压整压电路）
串联型直流稳压电路

模拟电路功能
（1）放大电路：用于信号的电压、电流或功率放大。
（2）滤波电路：用于信号的提取、变换或抗干扰。
（3）运算电路：完成信号的比例、加、减、乘、除、积分、微分、对数、指数等运算。
（4）信号转换电路：用于将电流信号转换成电压信号或将电压信号转换为电流信号、将直流信号转换为交流信号或将交流信号转换为直流信号、将直流电压转换成与之成正比的频率……
（5）信号发生电路：用于产生正弦波、矩形波、三角波、锯齿波。
（6）直流电源：将220V、50Hz交流电转换成不同输出电压和电流的直流电，作为各种电子线路的供电电源。
分类

模拟电路可分为标准模拟电路和专用模拟电路(application spacific analog IC)两大类，前者占市场的37%，后者占63%，据ICInsight公司报道，2000年两者合计达310亿美元，比上年大幅增长40%，预计今年将续增23%，达380亿美元。又据WSTS(世界半导体贸易统计协会2012年秋季最新预测，世界模拟电路市场2000年为306.3亿美元，2013年增长20%，达368.8亿美元，1999~2003年间的年均增长率为19.5%。标准模拟电路包括放大器接口电路、数据转换器、比较器、稳压器和基准电路等。2000年共计114亿美元，其中稳压器和基准电路比例最大，占整个模拟电路市场的13%，随后为放大器，占10%，接口电路8%，数据转换器6%，比较器1%。专用模拟电路市场是指在消费类电子产品、计算机、通信、汽车和工业其他部门应用的电路。2000年共计192亿美元在整个模拟电路市场上，通信用专用模拟电路占22%，消费类占16%，汽车用占9%，计算机占8%，工业和其他应用占7%。

数字电路

用数字信号完成对数字量进行算术运算和逻辑运算的电路称为数字电路，或数字系统。由于它具有逻辑运算和逻辑处理功能，所以又称数字逻辑电路。现代的数字电路由半导体工艺制成的若干数字集成器件构造而成。逻辑门是数字逻辑电路的基本单元。存储器是用来存储二进制数据的数字电路。从整体上看，数字电路可以分为组合逻辑电路和时序逻辑电路两大类。数字电路中研究的主要问题是输出信号的状态（“0”或“1”）和输入信号（“0”或“1”）之间的逻辑关系，即电路的逻辑功能。
数字电路的研究方法是逻辑分析和逻辑设计，所需要的工具是逻辑代数。 （在正逻辑下，“0”是低电平，“1”是高电平，高低电平没有明确的界限）。数字电路主要研究对象是电路的输出与输入之间的逻辑关系，因而在数字电路中不能采用模拟电路的分析方法，例如，小信号模型分析法。由于数字电路中的器件主要工作在开关状态，因而采用的分析工具主要是逻辑代数，用功能表、真值表、逻辑表达式、波形图等来表达电路的主要功能。随着计算技术的发展，为了分析、仿真与设计数字电路或数字系统，还可以采用硬件描述语言，使用如ABEL语言等软件，借助计算机来分析、仿真与设计数字系统。

从前面的介绍，大家已经了解到数字电路是以二值数字逻辑为基础的，其工作信号是离散的数字信号。电路中的电子晶体管工作于开关状态，时而导通，时而截止。
数字电路的发展与模拟电路一样经历了由电子管、半导体分立器件到集成电路等几个时代。但其发展比模拟电路发展的更快。从60年代开始，数字集成器件以双极型工艺制成了小规模逻辑器件。随后发展到中规模逻辑器件；70年代末，微处理器的出现，使数字集成电路的性能产生质的飞跃。
数字集成器件所用的材料以硅材料为主，在高速电路中，也使用化合物半导体材料，例如砷化镓等。
逻辑门是数字电路中一种重要的逻辑单元电路 。TTL逻辑门电路问世较早，其工艺经过不断改进，至今仍为主要的基本逻辑器件之一。随着CMOS工艺的发展，TTL的主导地位受到了动摇，有被CMOS器件所取代的趋势。
近几年来，可编程逻辑器件PLD特别是现场可编程门阵列FPGA的飞速进步，使数字电子技术开创了新局面，不仅规模大，而且将硬件与软件相结合，使器件的功能更加完善，使用更灵活。
数字电路或数字集成电路是由许多的逻辑门组成的复杂电路。与模拟电路相比，它主要进行数字信号的处理（即信号以0与1两个状态表示），因此抗干扰能力较强。数字集成电路有各种门电路、触发器以及由它们构成的各种组合逻辑电路和时序逻辑电路。一个数字系统一般由控制部件和运算部件组成，在时脉的驱动下，控制部件控制运算部件完成所要执行的动作。通过模拟数字转换器、数字模拟转换器，数字电路可以和模拟电路互相连接。

分类：

组合逻辑电路
简称组合电路，它由最基本的逻辑门电路组合而成。特点是：输出值只与当时的输入值有关，即输出惟一地由当时的输入值决定。电路没有记忆功能，输出状态随着输入状态的变化而变化，类似于电阻性电路，如加法器、译码器、编码器、数据选择器等都属于此类。

加法器是产生数的和的装置。加数和被加数为输入，和数与进位为输出的装置为半加器。若加数、被加数与低位的进位数为输入，而和数与进位为输出则为全加器。常用作计算机算术逻辑部件，执行逻辑操作、移位与指令调用。在电子学中，加法器是一种数位电路，其可进行数字的加法计算。在现代的电脑中，加法器存在于算术逻辑单元（ALU）之中。 加法器可以用来表示各种数值，如：BCD、加三码，主要的加法器是以二进制作运算。由于负数可用二的补数来表示，所以加减器也就不那么必要。

译码器是一类多输入多输出组合逻辑电路器件，其可以分为：变量译码和显示译码两类。 变量译码器一般是一种较少输入变为较多输出的器件，常见的有n线-2^n线译码和8421BCD码译码两类；显示译码器用来将二进制数转换成对应的七段码，一般其可分为驱动LED和驱动LCD两类。译码器是一种具有“翻译”功能的逻辑电路，这种电路能将输入二进制代码的各种状态，按照其原意翻译成对应的输出信号。有一些译码器设有一个和多个使能控制输入端，又成为片选端，用来控制允许译码或禁止译码。

编码器（encoder）是将信号（如比特流）或数据进行编制、转换为可用以通讯、传输和存储的信号形式的设备。编码器把角位移或直线位移转换成电信号，前者称为码盘，后者称为码尺。按照读出方式编码器可以分为接触式和非接触式两种；按照工作原理编码器可分为增量式和绝对式两类。增量式编码器是将位移转换成周期性的电信号，再把这个电信号转变成计数脉冲，用脉冲的个数表示位移的大小。绝对式编码器的每一个位置对应一个确定的数字码，因此它的示值只与测量的起始和终止位置有关，而与测量的中间过程无关。

时序逻辑电路
简称时序电路，它是由最基本的逻辑门电路加上反馈逻辑回路（输出到输入）或器件组合而成的电路，与组合电路最本质的区别在于时序电路具有记忆功能。时序电路的特点是：输出不仅取决于当时的输入值，而且还与电路过去的状态有关。它类似于含储能元件的电感或电容的电路，如触发器、锁存器、计数器、移位寄存器、储存器等电路都是时序电路的典型器件。
按电路有无集成元器件来分，可分为分立元件数字电路和集成数字电路。
按集成电路的集成度进行分类，可分为小规模集成数字电路(SSI)、中规模集成数字电路(MSI)、大规模集成数字电路(LSI)和超大规模集成数字电路(VLSI)。
按构成电路的半导体器件来分类，可分为双极型数字电路和单极型数字电路。

特点：
1、 同时具有算术运算和逻辑运算功能
数字电路是以二进制逻辑代数为数学基础，使用二进制数字信号，既能进行算术运算又能方便地进行逻辑运算（与、或、非、判断、比较、处理等），因此极其适合于运算、比较、存储、传输、控制、决策等应用。
2、 实现简单，系统可靠
以二进制作为基础的数字逻辑电路，可靠性较强。电源电压的小的波动对其没有影响，温度和工艺偏差对其工作的可靠性影响也比模拟电路小得多。
3、 集成度高，功能实现容易
集成度高，体积小，功耗低是数字电路突出的优点之一。电路的设计、维修、维护灵活方便，随着集成电路技术的高速发展，数字逻辑电路的集成度越来越高，集成电路块的功能随着小规模集成电路（SSI）、中规模集成电路（MSI）、大规模集成电路（LSI）、超大规模集成电路（VLSI）的发展也从元件级、器件级、部件级、板卡级上升到系统级。电路的设计组成只需采用一些标准的集成电路块单元连接而成。对于非标准的特殊电路还可以使用可编程序逻辑阵列电路，通过编程的方法实现任意的逻辑功能。

触发器 在实际的数字系统中往往包含大量的存储单元，而且经常要求他们在同一时刻同步动作，为达到这个目的，在每个存储单元电路上引入一个时钟脉冲（CLK）作为控制信号，只有当CLK到来时电路才被“触发”而动作，并根据输入信号改变输出状态。把这种在时钟信号触发时才能动作的存储单元电路称为触发器，以区别没有时钟信号控制的锁存器。常见的有 学名“双稳态多谐振荡器（Bistable Multivibrator）”。触发器（Flip Flop）是一种可以存储电路状态的电子元件。最简单的是由两个或非门，两个输入端和两个输出端组成的RS触发器（见图2）。复杂一些的有带时钟（CLK）段和D（Data）端，在CLK端为高电平时跟随D端状态，而在CLK端变为低电平的瞬间锁存信号的D触发器。更常用的是两个简单D触发器级联而成的在时钟下跳沿锁存信号的边缘D触发器，广泛应用于计数器、运算器、存储器等电子部件。

      锁存器(Latch)是一种对脉冲电平敏感的存储单元电路，它们可以在特定输入脉冲电平作用下改变状态。锁存，就是把信号暂存以维持某种电平状态。锁存器的最主要作用是缓存，其次完成高速的控制器与慢速的外设的不同步问题，再其次是解决驱动的问题，最后是解决一个 I/O 口既能输出也能输入的问题。锁存器是利用电平控制数据的输入，它包括不带使能控制的锁存器和带使能控制的锁存器。

计数器 计数是一种最简单基本的运算，计数器就是实现这种运算的逻辑电路，计数器在数字系统中主要是对脉冲的个数进行计数，以实现测量、计数和控制的功能，同时兼有分频功能，计数器是由基本的计数单元和一些控制门所组成，计数单元则由一系列具有存储信息功能的各类触发器构成，这些触发器有RS触发器、T触发器、D触发器及JK触发器等。计数器在数字系统中应用广泛，如在电子计算机的控制器中对指令地址进行计数，以便顺序取出下一条指令，在运算器中作乘法、除法运算时记下加法、减法次数，又如在数字仪器中对脉冲的计数等等。计数器是在数字电子技术中应用的最多的时序逻辑电路。计数器不仅能用于对时钟脉冲计数，还可以用于分频、定时、产生节拍脉冲和脉冲序列以及进行数字运算等。但是并无法显示计算结果，一般都是要通过外接LCD或LED屏才能显示。

寄存器的基本单元是 D触发器，按照其用途分为基本寄存器和移位寄存器。基本的寄存器是由 D触发器组成，在 CP 脉冲作用下，每个 D触发器能够寄存一位二进制码。在 D=0 时，寄存器储存为 0，在 D=1 时，寄存器储存为 1。在低电平为 0、高电平为 1 时，需将信号源与 D 间连接一反相器，这样就可以完成对数据的储存。移位寄存器按照移位方向可以分为单向移位寄存器和双向移位寄存器，单向移位寄存器是由多个 D 触发器串接而成,在串口 Di 输入需要储存的数据，触发器 FF0 就能够储存当前需要储存数据，在 CP 发出一次时钟控制脉冲时，串口 Di 同时输入第二个需要储存是的数据，而第一个数据则储存到触发器 FF1 中。双向移位寄存器按图中方式排列，调换连接端顺序，可以控制寄存器向左移位，增加控制电路可以使寄存器右移，这样构成双向移位寄存器。