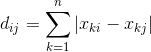距离度量

在机器学习算法中，常根据样本间的相似度或距离来判断样本的归属或样本之间的相似性，对于不同的问题，具体哪种相似度/距离更适合取决于应用问题的特性。

1、闵可夫斯基距离： 

定义1、给定样本集合X，X是n维实数向量空间  中点的集合，其中  ,样本  与样本  的闵科夫斯基距离定义为：

          

2、欧式距离：

当闵可夫斯基距离中的p=2时，称为欧氏距离，即

          

欧氏距离为n维空间中两个点之间的真实距离

3、曼哈顿距离：

当闵可夫斯基距离中的p=1时，称为曼哈顿距离，即

          

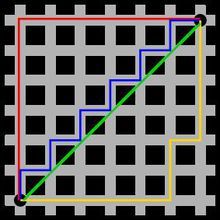
如下图，绿色线段表示两点直线距离，即欧式距离，而红为曼哈顿距离，蓝色和黄色为等价的曼哈顿距离，曼哈顿距离为：两个点在标准坐标系上的绝对轴距总和。

          

4、切比雪夫距离：

当  时称为切比雪夫距离，取各个坐标数值差的绝对值的最大值，即

          

且比雪夫距离为各坐标数值差的最大值。国际象棋棋盘上二个位置间的切比雪夫距离是指王要从一个位子移至另一个位子需要走的步数，如下图：

          

5、马氏距离：

定义：给定一个样本集合X，  ,其协方差矩阵记作S，样本  与样本  之间的马氏距离 定义为： 当S为单位矩阵时，即样本数据的各个分量相互独立且各个分量的方差为1时，可以看出，马氏距离就是欧式距离

可以发现，协方差矩阵为单位矩阵，即如果去掉马氏距离中的协方差矩阵，就为欧氏距离。那么，协方差矩阵在这里的意义是什么呢？

首先要说一下欧式距离的缺点：欧式距离将样品的不同属性（即各指标或各变量）之间的差别等同看待，这一点有时不能满足实际要求，比如身高和体重，两者之间时关联的，但这两个变量拥有不同的单位标准。比如身高用米，而体重用千克，变化1米和变化1kg在欧氏距离中，这将会算作相同的差距，但实际相差巨大。

马氏距离不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关，由标准化数据和中心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。

缺点：它的缺点是夸大了变化微小的变量的作用，受协方差矩阵不稳定的影响，马氏距离并不总是能顺利计算出。

马氏距离在回归分析中，是测量某一自变量的观测量与同一自变量所有观测量平均值差异的统计量，此值越大，说明该观测量为影响点的可能性越大。

6、皮尔逊相关系数：

样本  与样本  之间的相关系数定义为：

          

两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商

7、夹角余弦：

样本  与样本  的夹角余弦定义为：

          

举个栗子：

有5个国家的国民生产总值分别为 10, 20, 30, 50 和 80 亿美元。 假设这5个国家 (顺序相同) 的贫困百分比分别为 11%, 12%, 13%, 15%, and 18% 。 令x和y分别为包含上述5个数据的向量:x= (1, 2, 3, 5, 8) 和y= (0.11, 0.12, 0.13, 0.15, 0.18)。

计算两个向量之间的夹角  余弦：

          

仔细观察上面x,y两个变量，他们其实是完全相关的：y=0.01x + 0.1；计算x,y的皮尔逊相关系数,等于1，那么，将变量数据中心化后，得到的夹角余弦值也为1，即：夹角余弦与皮尔逊相关系数的区别只在于中心化。

以上几个概念都提及了协方差，协方差是一个反映两个随机变量相关程度的指标，如果一个变量跟随着另一个变量同时变大或者变小，那么这两个变量的协方差就是正值，反之相反。