终于来到了最终的大BOSS,卷积神经网络~
这里我想还是主要关注代码的实现,具体的CNN的知识点想以后在好好写一写,CNN的代码关键就是要加上卷积层和池话层.
一、卷积层
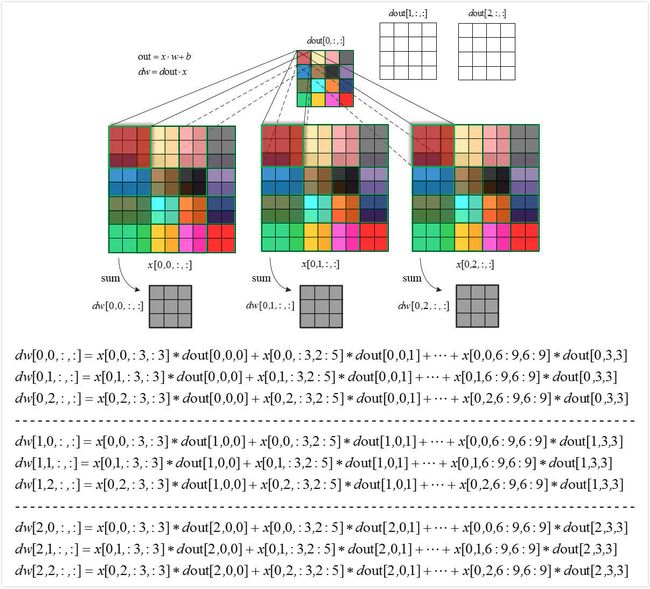
卷积层的前向传播还是比较容易的,我们主要关注的是反向传播,看下图就知道了:
def conv_forward_naive(x, w, b, conv_param): stride, pad = conv_param['stride'], conv_param['pad'] N, C, H, W = x.shape F, C, HH, WW = w.shape x_padded = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), mode='constant') #补零 H_new = 1 + (H + 2 * pad - HH) / stride W_new = 1 + (W + 2 * pad - WW) / stride s = stride out = np.zeros((N, F, H_new, W_new)) for i in xrange(N): # ith image for f in xrange(F): # fth filter for j in xrange(H_new): for k in xrange(W_new): out[i, f, j, k] = np.sum(x_padded[i, :, j*s:HH+j*s, k*s:WW+k*s] * w[f]) + b[f]#对应位相乘 cache = (x, w, b, conv_param) return out, cache def conv_backward_naive(dout, cache): x, w, b, conv_param = cache pad = conv_param['pad'] stride = conv_param['stride'] F, C, HH, WW = w.shape N, C, H, W = x.shape H_new = 1 + (H + 2 * pad - HH) / stride W_new = 1 + (W + 2 * pad - WW) / stride dx = np.zeros_like(x) dw = np.zeros_like(w) db = np.zeros_like(b) s = stride x_padded = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant') dx_padded = np.pad(dx, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant') for i in xrange(N): # ith image for f in xrange(F): # fth filter for j in xrange(H_new): for k in xrange(W_new): window = x_padded[i, :, j*s:HH+j*s, k*s:WW+k*s] db[f] += dout[i, f, j, k] dw[f] += window * dout[i, f, j, k] dx_padded[i, :, j*s:HH+j*s, k*s:WW+k*s] += w[f] * dout[i, f, j, k]#上面的式子,关键就在于+号 # Unpad dx = dx_padded[:, :, pad:pad+H, pad:pad+W] return dx, dw, db
和http://www.cnblogs.com/tornadomeet/p/3468450.html中提到的一样,卷积层的BP算法就是这么计算的,也就是一个正统的卷积操作
二、pooling层
def max_pool_forward_naive(x, pool_param): HH, WW = pool_param['pool_height'], pool_param['pool_width'] s = pool_param['stride'] N, C, H, W = x.shape H_new = 1 + (H - HH) / s W_new = 1 + (W - WW) / s out = np.zeros((N, C, H_new, W_new)) for i in xrange(N): for j in xrange(C): for k in xrange(H_new): for l in xrange(W_new): window = x[i, j, k*s:HH+k*s, l*s:WW+l*s] out[i, j, k, l] = np.max(window) cache = (x, pool_param) return out, cache def max_pool_backward_naive(dout, cache): x, pool_param = cache HH, WW = pool_param['pool_height'], pool_param['pool_width'] s = pool_param['stride'] N, C, H, W = x.shape H_new = 1 + (H - HH) / s W_new = 1 + (W - WW) / s dx = np.zeros_like(x) for i in xrange(N): for j in xrange(C): for k in xrange(H_new): for l in xrange(W_new): window = x[i, j, k*s:HH+k*s, l*s:WW+l*s] m = np.max(window) #获得之前的那个值,这样下面只要windows==m就能得到相应的位置 dx[i, j, k*s:HH+k*s, l*s:WW+l*s] = (window == m) * dout[i, j, k, l] return dx
三、与之前的区别
这里BN算法与之前是不太一样的,因为网络的输入变成了saptail的
def spatial_batchnorm_forward(x, gamma, beta, bn_param): N, C, H, W = x.shape x_new = x.transpose(0, 2, 3, 1).reshape(N*H*W, C)#分成不同的channel来算,所以可以直接用之前的代码 out, cache = batchnorm_forward(x_new, gamma, beta, bn_param) out = out.reshape(N, H, W, C).transpose(0, 3, 1, 2) return out, cache def spatial_batchnorm_backward(dout, cache): N, C, H, W = dout.shape dout_new = dout.transpose(0, 2, 3, 1).reshape(N*H*W, C) dx, dgamma, dbeta = batchnorm_backward(dout_new, cache) dx = dx.reshape(N, H, W, C).transpose(0, 3, 1, 2) return dx, dgamma, dbeta
四、总结
assignment2终于弄完了,总的来说..numpy还是要多熟悉,具体的操作也要熟悉。卷积层的前向传播很好理解,反向传播和之前的区别不大,只不过需要做一个卷积的操作。