机器学习实战—— Chap06.SVM

import matplotlib.pyplot as plt
import numpy as np
import random

"""
Desc:
    读取数据

Parameters:
    fileName - 文件名
    
Returns:
    dataMat - 数据矩阵
    labelMat - 数据标签
"""
def loadDataSet(fileName):
    # 数据矩阵
    dataMat = []
    # 标签向量
    labelMat = []
    # 打开文件
    fr = open(fileName)
    # 逐行读取
    for line in fr.readlines():
        # 去掉每一行首尾的空白符，例如'\n','\r','\t',' '
        # 将每一行内容根据'\t'符进行切片
        lineArr = line.strip().split('\t')
        # 添加数据(100个元素排成一行)
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        # 添加标签(100个元素排成一行)
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat


"""
Desc:
    随机选择alpha_j

Parameters:
    i - alpha
    m - alpha参数个数
    
Returns:
    j - 返回选定的数字
"""
def selectJrand(i, m):
    j = i
    while(j == i):
        # uniform()方法将随机生成一个实数，它在[x, y)范围内
        j = int(random.uniform(0, m))
    return j


"""
Desc:
    修剪alpha

Parameters:
    aj - alpha值
    H - alpha上限
    L - alpha下限
    
Returns:
    aj - alpha值
"""
def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj


"""
Desc:
    简化版SMO算法

Parameters:
    dataMatIn - 数据矩阵
    classLabels - 数据标签
    C - 松弛变量
    toler - 容错率
    maxIter - 最大迭代次数
    
Returns:
    None
"""
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    # 转换为numpy的mat矩阵存储(100,2)
    dataMatrix = np.mat(dataMatIn)
    # 转换为numpy的mat矩阵存储并转置(100,1)
    labelMat = np.mat(classLabels).transpose()
    # 初始化b参数，统计dataMatrix的维度,m:行；n:列
    b = 0
    # 统计dataMatrix的维度,m:100行；n:2列
    m, n = np.shape(dataMatrix)
    # 初始化alpha参数，设为0
    alphas = np.mat(np.zeros((m, 1)))
    # 初始化迭代次数
    iter_num = 0
    # 最多迭代maxIter次
    while(iter_num < maxIter):
        alphaPairsChanged = 0
        for i in range(m):
            # 步骤1：计算误差Ei
            # multiply(a,b)就是个乘法，如果a,b是两个数组，那么对应元素相乘
            # .T为转置
            fxi = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
            # 误差项计算公式
            Ei = fxi - float(labelMat[i])
            # 优化alpha，设定一定的容错率
            if((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):
                # 随机选择另一个alpha_i成对比优化的alpha_j
                j = selectJrand(i, m)
                # 步骤1，计算误差Ej
                fxj = float(np.multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b
                # 误差项计算公式
                Ej = fxj - float(labelMat[j])
                # 保存更新前的alpha值，使用深拷贝(完全拷贝)A深层拷贝为B，A和B是两个独立的个体
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()
                # 步骤2：计算上下界H和L
                if(labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j]  -alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if(L == H):
                    print("L == H")
                    continue
                # 步骤3：计算eta
                eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - dataMatrix[i, :] * dataMatrix[i, :].T - dataMatrix[j, :] * dataMatrix[j, :].T
                if eta >= 0:
                    print("eta>=0")
                    continue
                # 步骤4：更新alpha_j
                alphas[j] -= labelMat[j] * (Ei - Ej) / eta
                # 步骤5：修剪alpha_j
                alphas[j] = clipAlpha(alphas[j], H, L)
                if(abs(alphas[j] - alphaJold) < 0.00001):
                    print("alpha_j变化太小")
                    continue
                # 步骤6：更新alpha_i
                alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j])
                # 步骤7：更新b_1和b_2
                b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[i, :].T
                b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[j, :].T - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].T
                # 步骤8：根据b_1和b_2更新b
                if(0 < alphas[i] < C):
                    b = b1
                elif(0 < alphas[j] < C):
                    b = b2
                else:
                    b = (b1 + b2) / 2.0
                # 统计优化次数
                alphaPairsChanged += 1
                # 打印统计信息
                print("第%d次迭代 样本：%d， alpha优化次数：%d" % (iter_num, i, alphaPairsChanged))
        # 更新迭代次数
        if(alphaPairsChanged == 0):
            iter_num += 1
        else:
            iter_num = 0
        print("迭代次数：%d" % iter_num)
    return b, alphas
                

"""
Desc:
    计算w

Returns:
    dataMat - 数据矩阵
    labelMat - 数据标签
    alphas - alphas值
    
Returns:
    w - 直线法向量
"""
def get_w(dataMat, labelMat, alphas):
    alphas, dataMat, labelMat = np.array(alphas), np.array(dataMat), np.array(labelMat)
    # 我们不知道labelMat的shape属性是多少，
    # 但是想让labelMat变成只有一列，行数不知道多少，
    # 通过labelMat.reshape(1, -1)，Numpy自动计算出有100行，
    # 新的数组shape属性为(100, 1)
    # np.tile(labelMat.reshape(1, -1).T, (1, 2))将labelMat扩展为两列(将第1列复制得到第2列)
    # dot()函数是矩阵乘，而*则表示逐个元素相乘
    # w = sum(alpha_i * yi * xi)
    w = np.dot((np.tile(labelMat.reshape(1, -1).T, (1, 2)) * dataMat).T, alphas)
    return w.tolist()


"""
Desc:
    分类结果可视化

Returns:
    dataMat - 数据矩阵
    w - 直线法向量
    b - 直线截距
    
Returns:
    None
"""
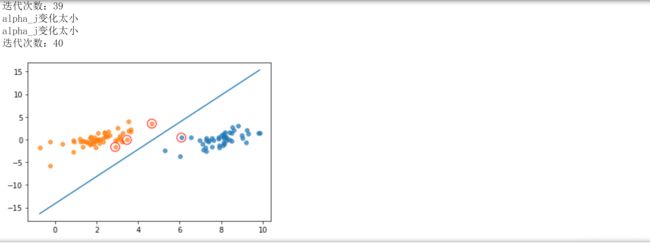
def showClassifer(dataMat, w, b):
    # 正样本
    data_plus = []
    # 负样本
    data_minus = []
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    # 转换为numpy矩阵
    data_plus_np = np.array(data_plus)
    # 转换为numpy矩阵
    data_minus_np = np.array(data_minus)
    # 正样本散点图（scatter）
    # transpose转置
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)
    # 负样本散点图（scatter）
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7)
    # 绘制直线
    x1 = max(dataMat)[0]
    x2 = min(dataMat)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    y1, y2 = (-b - a1 * x1) / a2, (-b - a1 * x2) / a2
    plt.plot([x1, x2], [y1, y2])
    # 找出支持向量点
    # enumerate在字典上是枚举、列举的意思
    for i, alpha in enumerate(alphas):
        # 支持向量机的点
        if(abs(alpha) > 0):
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolors='red')
    plt.show()   

if __name__ == '__main__':
    dataMat, labelMat = loadDataSet('testSet.txt')
    b, alphas = smoSimple(dataMat, labelMat, 0.6, 0.001, 40)
    w = get_w(dataMat, labelMat, alphas)
    showClassifer(dataMat, w, b)

import matplotlib.pyplot as plt
import numpy as np
import random

"""
Desc:
    维护所有需要操作的值

Parameters:
    dataMatIn - 数据矩阵
    classLabels - 数据标签
    C - 松弛变量
    toler - 容错率
    
Returns:
    None
"""
class optStruct:
    def __init__(self, dataMatIn, classLabels, C, toler):
        # 数据矩阵
        self.X = dataMatIn
        # 数据标签
        self.labelMat = classLabels
        # 松弛变量
        self.C = C
        # 容错率
        self.tol = toler
        # 矩阵的行数
        self.m = np.shape(dataMatIn)[0]
        # 根据矩阵行数初始化alphas矩阵，一个m行1列的全零列向量
        self.alphas = np.mat(np.zeros((self.m, 1)))
        # 初始化b参数为0
        self.b = 0
        # 根据矩阵行数初始化误差缓存矩阵，第一列为是否有效标志位，第二列为实际的误差E的值
        self.eCache = np.mat(np.zeros((self.m, 2)))


"""
Desc:
    读取数据

Parameters:
    fileName - 文件名
    
Returns:
    dataMat - 数据矩阵
    labelMat - 数据标签
"""
def loadDataSet(fileName):
    # 数据矩阵
    dataMat = []
    # 标签向量
    labelMat = []
    # 打开文件
    fr = open(fileName)
    # 逐行读取
    for line in fr.readlines():
        # 去掉每一行首尾的空白符，例如'\n','\r','\t',' '
        # 将每一行内容根据'\t'符进行切片
        lineArr = line.strip().split('\t')
        # 添加数据(100个元素排成一行)
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        # 添加标签(100个元素排成一行)
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat


"""
Desc:
    计算误差

Parameters:
    oS - 数据结构
    k - 标号为k的数据
    
Returns:
    Ek - 标号为k的数据误差
"""
def calcEk(oS, k):
    # multiply(a,b)就是个乘法，如果a,b是两个数组，那么对应元素相乘
    # .T为转置
    fXk = float(np.multiply(oS.alphas, oS.labelMat).T * (oS.X * oS.X[k, :].T) + oS.b)
    # 计算误差项
    Ek = fXk - float(oS.labelMat[k])
    # 返回误差项
    return Ek


"""
Desc:
    随机选择alpha_j

Parameters:
    i - alpha_i的索引值
    m - alpha参数个数
    
Returns:
    j - alpha_j的索引值

"""
def selectJrand(i, m):
    j = i
    while(j == i):
        # uniform()方法将随机生成一个实数，它在[x, y)范围内
        j = int(random.uniform(0, m))
    return j


"""
Desc:
    内循环启发方式2

Parameters:
    i - 标号为i的数据的索引值
    oS - 数据结构
    Ei - 标号为i的数据误差
    
Returns:
    j - 标号为j的数据的索引值
    maxK - 标号为maxK的数据的索引值
    Ej - 标号为j的数据误差

"""
def selectJ(i, oS, Ei):
    # 初始化
    maxK = -1
    maxDeltaE = 0
    Ej = 0
    # 根据Ei更新误差缓存
    oS.eCache[i] = [1, Ei]
    # 对一个矩阵.A转换为Array类型
    # 返回误差不为0的数据的索引值
    validEcacheList = np.nonzero(oS.eCache[:, 0].A)[0]
    # 有不为0的误差
    if(len(validEcacheList) > 1):
        # 遍历，找到最大的Ek
        for k in validEcacheList:
            # 不计算k==i节省时间
            if k == i:
                continue
            # 计算Ek
            Ek = calcEk(oS, k)
            # 计算|Ei - Ek|
            deltaE = abs(Ei - Ek)
            # 找到maxDeltaE
            if(deltaE > maxDeltaE):
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        # 返回maxK，Ej
        return maxK, Ej
    # 没有不为0的误差
    else:
        # 随机选择alpha_j的索引值
        j = selectJrand(i, oS.m)
        # 计算Ej
        Ej = calcEk(oS, j)
    # 返回j，Ej
    return j, Ej


"""
Desc:
    计算Ek,并更新误差缓存

Parameters:
    oS - 数据结构
    k - 标号为k的数据的索引值
    
Returns:
    None
"""
def updateEk(oS, k):
    # 计算Ek
    Ek = calcEk(oS, k)
    # 更新误差缓存
    oS.eCache[k] = [1, Ek]
    
    
"""
Desc:
    修剪alpha_j

Parameters:
    aj - alpha_j值
    H - alpha上限
    L - alpha下限
    
Returns:
    aj - alpha_j值
"""
def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj


"""
Desc:
    优化的SMO算法

Parameters:
    i - 标号为i的数据的索引值
    oS - 数据结构
    
Returns:
    1 - 有任意一对alpha值发生变化
    0 - 没有任意一对alpha值发生变化或变化太小
"""
def innerL(i, oS):
    # 步骤1：计算误差Ei
    Ei = calcEk(oS, i)
    # 优化alpha,设定一定的容错率
    if((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
        # 使用内循环启发方式2选择alpha_j,并计算Ej
        j, Ej = selectJ(i, oS, Ei)
        # 保存更新前的alpha值，使用深层拷贝
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        # 步骤2：计算上界H和下界L
        if(oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L == H:
            print("L == H")
            return 0
        # 步骤3：计算eta
        eta = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - oS.X[j, :] * oS.X[j, :].T
        if eta >= 0:
            print("eta >= 0")
            return 0
        # 步骤4：更新alpha_j
        oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
        # 步骤5：修剪alpha_j
        oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
        # 更新Ej至误差缓存
        updateEk(oS, j)
        if(abs(oS.alphas[j] - alphaJold) < 0.00001):
            print("alpha_j变化太小")
            return 0
        # 步骤6：更新alpha_i
        oS.alphas[i] += oS.labelMat[i] * oS.labelMat[j] * (alphaJold - oS.alphas[j])
        # 更新Ei至误差缓存
        updateEk(oS, i)
        # 步骤7：更新b_1和b_2:
        b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[i, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[i, :].T
        b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[j, :].T
        # 步骤8：根据b_1和b_2更新b
        if(0 < oS.alphas[i] < oS.C):
            oS.b = b1
        elif(0 < oS.alphas[j] < oS.C):
            oS.b = b2
        else:
            oS.b = (b1 + b2) / 2.0
        return 1
    else:
        return 0
    
    
"""
Desc:
    完整的线性SMO算法

Parameters:
    dataMatIn - 数据矩阵
    classLabels - 数据标签
    C - 松弛变量
    toler - 容错率
    maxIter - 最大迭代次数
    
Returns:
    oS.b - SMO算法计算的b
    oS.alphas - SMO算法计算的alphas
"""
def smoP(dataMatIn, classLabels, C, toler, maxIter):
    # 初始化数据结构
    oS = optStruct(np.mat(dataMatIn), np.mat(classLabels).transpose(), C, toler)
    # 初始化当前迭代次数
    iter = 0
    entrieSet = True
    alphaPairsChanged = 0
    # 遍历整个数据集alpha都没有更新或者超过最大迭代次数，则退出循环
    while(iter < maxIter) and ((alphaPairsChanged > 0) or (entrieSet)):
        alphaPairsChanged = 0
        # 遍历整个数据集
        if entrieSet:
            for i in range(oS.m):
                # 使用优化的SMO算法
                alphaPairsChanged += innerL(i, oS)
                print("全样本遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter, i, alphaPairsChanged))
            iter += 1
        # 遍历非边界值
        else:
            # 遍历不在边界0和C的alpha
            nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i, oS)
                print("非边界遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter, i, alphaPairsChanged))
            iter += 1
        # 遍历一次后改为非边界遍历
        if entrieSet:
            entrieSet = False
        # 如果alpha没有更新，计算全样本遍历
        elif(alphaPairsChanged == 0):
            entrieSet = True
        print("迭代次数:%d" % iter)
    # 返回SMO算法计算的b和alphas
    return oS.b, oS.alphas
                
    
"""
Desc:
    分类结果可视化

Returns:
    dataMat - 数据矩阵
    classLabels - 数据标签
    w - 直线法向量
    b - 直线截距
    
Returns:
    None
"""
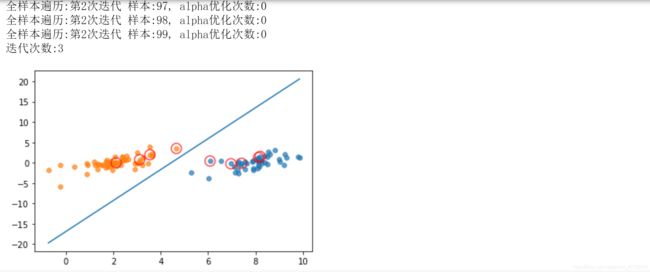
def showClassifer(dataMat, classLabels, w, b):
    # 正样本
    data_plus = []
    # 负样本
    data_minus = []
    for i in range(len(dataMat)):
        if classLabels[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    # 转换为numpy矩阵
    data_plus_np = np.array(data_plus)
    # 转换为numpy矩阵
    data_minus_np = np.array(data_minus)
    # 正样本散点图（scatter）
    # transpose转置
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)
    # 负样本散点图（scatter）
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7)
    # 绘制直线
    x1 = max(dataMat)[0]
    x2 = min(dataMat)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    y1, y2 = (-b - a1 * x1) / a2, (-b - a1 * x2) / a2
    plt.plot([x1, x2], [y1, y2])
    # 找出支持向量点
    # enumerate在字典上是枚举、列举的意思
    for i, alpha in enumerate(alphas):
        # 支持向量机的点
        if(abs(alpha) > 0):
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolors='red')
    plt.show()


"""
Desc:
    计算w

Returns:
    dataArr - 数据矩阵
    classLabels - 数据标签
    alphas - alphas值
    
Returns:
    w - 直线法向量
"""
def calcWs(alphas, dataArr, classLabels):
    X = np.mat(dataArr)
    labelMat = np.mat(classLabels).transpose()
    m, n = np.shape(X)
    w = np.zeros((n, 1))
    for i in range(m):
        w += np.multiply(alphas[i] * labelMat[i], X[i, :].T)
    return w    

if __name__ == '__main__':
    dataArr, classLabels = loadDataSet('testSet.txt')
    b, alphas = smoP(dataArr, classLabels, 0.6, 0.001, 40)
    w = calcWs(alphas, dataArr, classLabels)
    showClassifer(dataArr, classLabels, w, b)

import matplotlib.pyplot as plt
import numpy as np
import random

"""
类说明：维护所有需要操作的值

Parameters:
    dataMatIn - 数据矩阵
    classLabels - 数据标签
    C - 松弛变量
    toler - 容错率
    kTup - 包含核函数信息的元组，第一个参数存放该核函数类别，第二个参数存放必要的核函数需要用到的参数
    
Returns:
    None
"""
class optStruct:
    def __init__(self, dataMatIn, classLabels, C, toler, kTup):
        # 数据矩阵
        self.X = dataMatIn
        # 数据标签
        self.labelMat = classLabels
        # 松弛变量
        self.C = C
        # 容错率
        self.tol = toler
        # 矩阵的行数
        self.m = np.shape(dataMatIn)[0]
        # 根据矩阵行数初始化alphas矩阵，一个m行1列的全零列向量
        self.alphas = np.mat(np.zeros((self.m, 1)))
        # 初始化b参数为0
        self.b = 0
        # 根据矩阵行数初始化误差缓存矩阵，第一列为是否有效标志位，第二列为实际的误差E的值
        self.eCache = np.mat(np.zeros((self.m, 2)))
        # 初始化核K
        self.K = np.mat(np.zeros((self.m, self.m)))
        # 计算所有数据的核K
        for i in range(self.m):
            self.K[:, i] = kernelTrans(self.X, self.X[i, :], kTup)


"""
Desc:
    通过核函数将数据转换更高维空间

Parameters:
    X - 数据矩阵
    A - 单个数据的向量
    kTup - 包含核函数信息的元组
    
Returns:
    K - 计算的核K
"""
def kernelTrans(X, A, kTup):
    # 读取X的行列数
    m, n = np.shape(X)
    # K初始化为m行1列的零向量
    K = np.mat(np.zeros((m, 1)))
    # 线性核函数只进行内积
    if kTup[0] == 'lin':
        K = X * A.T
    # 高斯核函数，根据高斯核函数公式计算
    elif kTup[0] == 'rbf':
        for j in range(m):
            deltaRow = X[j, :] - A
            K[j] = deltaRow * deltaRow.T
        K = np.exp(K / (-1 * kTup[1] ** 2))
    else:
        raise NameError('核函数无法识别')
    return K
     
        
"""
Desc:
    读取数据

Parameters:
    fileName - 文件名
    
Returns:
    dataMat - 数据矩阵
    labelMat - 数据标签
"""
def loadDataSet(fileName):
    # 数据矩阵
    dataMat = []
    # 标签向量
    labelMat = []
    # 打开文件
    fr = open(fileName)
    # 逐行读取
    for line in fr.readlines():
        # 去掉每一行首尾的空白符，例如'\n','\r','\t',' '
        # 将每一行内容根据'\t'符进行切片
        lineArr = line.strip().split('\t')
        # 添加数据(100个元素排成一行)
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        # 添加标签(100个元素排成一行)
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat


"""
Desc:
    计算误差

Parameters:
    oS - 数据结构
    k - 标号为k的数据
    
Returns:
    Ek - 标号为k的数据误差
"""
def calcEk(oS, k):
    # multiply(a,b)就是个乘法，如果a,b是两个数组，那么对应元素相乘
    # .T为转置
    fXk = float(np.multiply(oS.alphas, oS.labelMat).T * oS.K[:, k]  + oS.b)
    # 计算误差项
    Ek = fXk - float(oS.labelMat[k])
    # 返回误差项
    return Ek


"""
Desc:
    随机选择alpha_j

Parameters:
    i - alpha_i的索引值
    m - alpha参数个数
    
Returns:
    j - alpha_j的索引值
"""
def selectJrand(i, m):
    j = i
    while(j == i):
        # uniform()方法将随机生成一个实数，它在[x, y)范围内
        j = int(random.uniform(0, m))
    return j


"""
Desc:
    内循环启发方式2

Parameters:
    i - 标号为i的数据的索引值
    oS - 数据结构
    Ei - 标号为i的数据误差
    
Returns:
    j - 标号为j的数据的索引值
    maxK - 标号为maxK的数据的索引值
    Ej - 标号为j的数据误差
"""
def selectJ(i, oS, Ei):
    # 初始化
    maxK = -1
    maxDeltaE = 0
    Ej = 0
    # 根据Ei更新误差缓存
    oS.eCache[i] = [1, Ei]
    # 对一个矩阵.A转换为Array类型
    # 返回误差不为0的数据的索引值
    validEcacheList = np.nonzero(oS.eCache[:, 0].A)[0]
    # 有不为0的误差
    if(len(validEcacheList) > 1):
        # 遍历，找到最大的Ek
        for k in validEcacheList:
            # 不计算k==i节省时间
            if k == i:
                continue
            # 计算Ek
            Ek = calcEk(oS, k)
            # 计算|Ei - Ek|
            deltaE = abs(Ei - Ek)
            # 找到maxDeltaE
            if(deltaE > maxDeltaE):
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        # 返回maxK，Ej
        return maxK, Ej
    # 没有不为0的误差
    else:
        # 随机选择alpha_j的索引值
        j = selectJrand(i, oS.m)
        # 计算Ej
        Ej = calcEk(oS, j)
    # 返回j，Ej
    return j, Ej


"""
Desc:
    计算Ek,并更新误差缓存

Parameters:
    oS - 数据结构
    k - 标号为k的数据的索引值
    
Returns:
    None
"""
def updateEk(oS, k):
    # 计算Ek
    Ek = calcEk(oS, k)
    # 更新误差缓存
    oS.eCache[k] = [1, Ek]
    
      
"""
Desc:
    修剪alpha_j

Parameters:
    aj - alpha_j值
    H - alpha上限
    L - alpha下限
    
Returns:
    aj - alpha_j值
"""
def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj


"""
Desc:
    优化的SMO算法

Parameters:
    i - 标号为i的数据的索引值
    oS - 数据结构
    
Returns:
    1 - 有任意一对alpha值发生变化
    0 - 没有任意一对alpha值发生变化或变化太小
"""
def innerL(i, oS):
    # 步骤1：计算误差Ei
    Ei = calcEk(oS, i)
    # 优化alpha,设定一定的容错率
    if((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
        # 使用内循环启发方式2选择alpha_j,并计算Ej
        j, Ej = selectJ(i, oS, Ei)
        # 保存更新前的alpha值，使用深层拷贝
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        # 步骤2：计算上界H和下界L
        if(oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L == H:
            print("L == H")
            return 0
        # 步骤3：计算eta
        eta = 2.0 * oS.K[i, j] - oS.K[i, i] - oS.K[j, j]
        if eta >= 0:
            print("eta >= 0")
            return 0
        # 步骤4：更新alpha_j
        oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
        # 步骤5：修剪alpha_j
        oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
        # 更新Ej至误差缓存
        updateEk(oS, j)
        if(abs(oS.alphas[j] - alphaJold) < 0.00001):
            print("alpha_j变化太小")
            return 0
        # 步骤6：更新alpha_i
        oS.alphas[i] += oS.labelMat[i] * oS.labelMat[j] * (alphaJold - oS.alphas[j])
        # 更新Ei至误差缓存
        updateEk(oS, i)
        # 步骤7：更新b_1和b_2:
        b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, i] - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[j, i]
        b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, j] - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[j, j]
        # 步骤8：根据b_1和b_2更新b
        if(0 < oS.alphas[i] < oS.C):
            oS.b = b1
        elif(0 < oS.alphas[j] < oS.C):
            oS.b = b2
        else:
            oS.b = (b1 + b2) / 2.0
        return 1
    else:
        return 0
    

"""
Desc:
    完整的线性SMO算法

Parameters:
    dataMatIn - 数据矩阵
    classLabels - 数据标签
    C - 松弛变量
    toler - 容错率
    maxIter - 最大迭代次数
    kTup - 包含核函数信息的元组
    
Returns:
    oS.b - SMO算法计算的b
    oS.alphas - SMO算法计算的alphas
"""
def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup = ('lin', 0)):
    # 初始化数据结构
    oS = optStruct(np.mat(dataMatIn), np.mat(classLabels).transpose(), C, toler, kTup)
    # 初始化当前迭代次数
    iter = 0
    entrieSet = True
    alphaPairsChanged = 0
    # 遍历整个数据集alpha都没有更新或者超过最大迭代次数，则退出循环
    while(iter < maxIter) and ((alphaPairsChanged > 0) or (entrieSet)):
        alphaPairsChanged = 0
        # 遍历整个数据集
        if entrieSet:
            for i in range(oS.m):
                # 使用优化的SMO算法
                alphaPairsChanged += innerL(i, oS)
                print("全样本遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter, i, alphaPairsChanged))
            iter += 1
        # 遍历非边界值
        else:
            # 遍历不在边界0和C的alpha
            nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i, oS)
                print("非边界遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter, i, alphaPairsChanged))
            iter += 1
        # 遍历一次后改为非边界遍历
        if entrieSet:
            entrieSet = False
        # 如果alpha没有更新，计算全样本遍历
        elif(alphaPairsChanged == 0):
            entrieSet = True
        print("迭代次数:%d" % iter)
    # 返回SMO算法计算的b和alphas
    return oS.b, oS.alphas


"""
Desc:
    测试函数

Parameters:
    k1 - 使用高斯核函数的时候表示到达率
    
Returns:
    None
"""
def testRbf(k1 = 1.3):
    # 加载训练集
    dataArr, labelArr = loadDataSet('testSetRBF.txt')
    # 根据训练集计算b, alphas
    b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 100, ('rbf', k1))
    datMat = np.mat(dataArr)
    labelMat = np.mat(labelArr).transpose()
    # 获得支持向量
    svInd = np.nonzero(alphas.A > 0)[0]
    sVs = datMat[svInd]
    labelSV = labelMat[svInd]
    print("支持向量个数:%d" % np.shape(sVs)[0])
    m, n = np.shape(datMat)
    errorCount = 0
    for i in range(m):
        # 计算各个点的核
        kernelEval = kernelTrans(sVs, datMat[i, :], ('rbf', k1))
        # 根据支持向量的点计算超平面，返回预测结果
        predict = kernelEval.T * np.multiply(labelSV, alphas[svInd]) + b
        # 返回数组中各元素的正负号，用1和-1表示，并统计错误个数
        if np.sign(predict) != np.sign(labelArr[i]):
            errorCount += 1
    # 打印错误率
    print('训练集错误率:%.2f%%' % ((float(errorCount) / m) * 100))
    # 加载测试集
    dataArr, labelArr = loadDataSet('testSetRBF2.txt')
    errorCount = 0
    datMat = np.mat(dataArr)
    labelMat = np.mat(labelArr).transpose()
    m, n = np.shape(datMat)
    for i in range(m):
        # 计算各个点的核
        kernelEval = kernelTrans(sVs, datMat[i, :], ('rbf', k1))
        # 根据支持向量的点计算超平面，返回预测结果
        predict = kernelEval.T * np.multiply(labelSV, alphas[svInd]) + b
        # 返回数组中各元素的正负号，用1和-1表示，并统计错误个数
        if np.sign(predict) != np.sign(labelArr[i]):
            errorCount += 1
    # 打印错误率
    print('训练集错误率:%.2f%%' % ((float(errorCount) / m) * 100))
    

"""
Desc:
    数据可视化

Parameters:
    dataMat - 数据矩阵
    labelMat - 数据标签
    
Returns:
    None
"""
def showDataSet(dataMat, labelMat):
    # 正样本
    data_plus = []
    # 负样本
    data_minus = []
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    # 转换为numpy矩阵
    data_plus_np = np.array(data_plus)
    # 转换为numpy矩阵
    data_minus_np = np.array(data_minus)
    # 正样本散点图（scatter）
    # transpose转置
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1])
    # 负样本散点图（scatter）
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1])
    # 显示
    plt.show()

if __name__ == '__main__':
    testRbf()